小虎最近研究自功率谱的意义和作用，发现自功率谱还可以进行信号的简谐分量分析的哦，这里小虎使用了MATLAB进行仿真的方法来展现结果。

什么是自功率谱

根据帕塞瓦尔定理(Parseval’s theorem)，在时域信号的总能量等于在频域信号的总能量。由随机信号经过傅里叶变换，再经过以下计算，可以求其自功率谱(Power spectrum)。
$$S_x(\omega )=\underset{T\to \infty }{\lim }\frac{1}{T}|X(\omega ){|}^2$$

参数设置

设采样数n=1000，采样时间fs=1000，采样间隔为t。然后利用两个三角函数和一个随机噪声信号相加得到模拟信号。两个三角函数信号分别为频率为40HZ和90HZ的正弦波信号。
$$\begin{gathered} w_0=2\times \pi \times f_0 \\ {y}_1=sin(80\pi t) \\ {y}_2=sin(180\pi t) \end{gathered}$$

结果

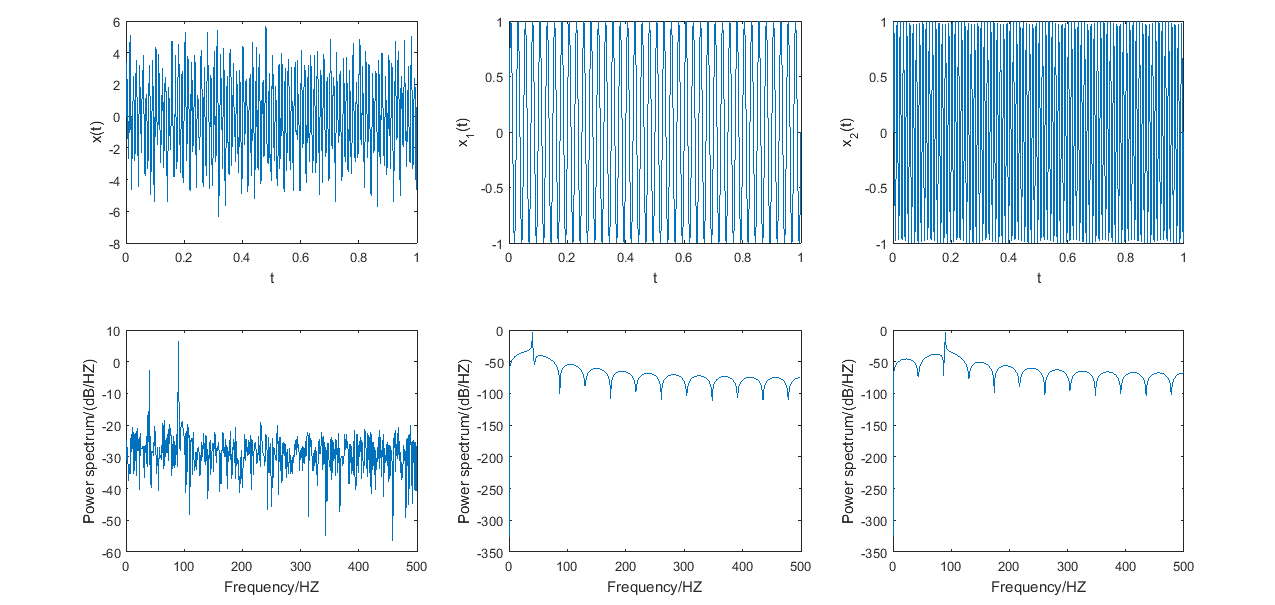
物理意义

• 可以从下面一行图中看到，后面两个三角函数的自功率谱分别在$f=40HZ$和$=90HZ$有个尖峰，这正是这两个三角函数的固有频率。
• 在下面一行第一个图中，可以看到模拟信号的自功率谱在$f=40HZ$和$=90HZ$也有两个尖峰，所以可以从这里读出原来的两个简谐信号的固有频率。

代码分析

函数构建。

fs=1000;
n=1001;
t=(0:n-1)/fs;
x_n=sin(2*pi*40*t)+3*sin(2*pi*90*t)+randn(size(t));

求自功率频谱。

[Px,w]=periodogram(x_n,[],1023,fs);

画原信号图、自功率谱图。

figure('color',[1 1 1]);
subplot(2,1,1);
plot(t,x_n);
xlabel('t');
ylabel('x(t)');
subplot(2,1,4);
plot(w,10*log10(Px));
xlabel('Frequency/HZ');
ylabel('Power spectrum/(dB/HZ)');

完整代码

fs=1000;
n=1001;
t=(0:n-1)/fs;
x_n=sin(2*pi*40*t)+3*sin(2*pi*90*t)+randn(size(t));
[Px,w]=periodogram(x_n,[],1023,fs);
figure('color',[1 1 1]);
subplot(2,1,1);
plot(t,x_n);
xlabel('t');
ylabel('x(t)');
subplot(2,1,4);
plot(w,10*log10(Px));
xlabel('Frequency/HZ');
ylabel('Power spectrum/(dB/HZ)');

参考文献

[1]张春华等，工程测试技术基础第二版

更多

信号处理趣学D0——系列专栏的说明与目录
信号处理趣学D1——相关函数的意义&利用自相关函数消除噪声
信号处理趣学D2——利用自相关函数对分析音频的周期变化
信号处理趣学D3——工程测试技术模拟信号采样
信号处理趣学D4——利用谐波叠加对周期方波进行逼近
信号处理趣学D5——利用仿真教你理解周期混叠和采样定理
信号处理趣学D6——利用MATLAB画出非周期函数的频谱图
信号处理趣学D7——自功率谱的物理意义&通过自功率谱分析原信号的简谐分量
信号处理趣学D8——关于拉氏变换和频谱图的那些事儿
信号处理趣学D9——教你仿真理解信号的调制和解调
信号处理趣学D10——简单理解过调失真（附例子和代码）
信号处理趣学D11——怎么避免信号调质过程的时候重叠失真？

最后

以上就是漂亮小蜜蜂为你收集整理的信号处理趣学D7——自功率谱的物理意义&通过自功率谱分析原信号的简谐分量什么是自功率谱参数设置结果代码分析完整代码参考文献更多的全部内容，希望文章能够帮你解决信号处理趣学D7——自功率谱的物理意义&通过自功率谱分析原信号的简谐分量什么是自功率谱参数设置结果代码分析完整代码参考文献更多所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。