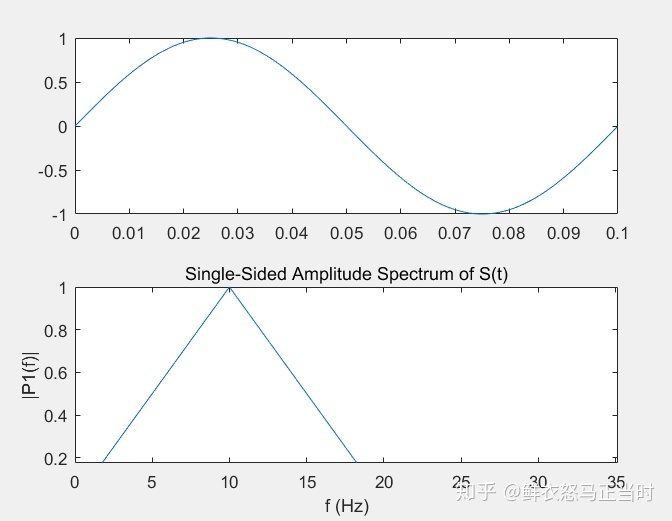
1.这是通常情况下,输入一个多频率成分的函数,然后得到傅里叶变换
clear;clc;
Fs = 10000; % 采样频率,要大于时域信号中最大频率的两倍
T = 1/Fs; % 采样周期,或者说是时域信号的时间步长,因为你处理的信号不会是连续的
L = 1000; % 信号长度,或者说你选取的信号离散点的个数,就是总共1000个时间点 由此知,频率分辨率为 1hz
t = (0:L-1)*T; % 时间相量,可以看成时域信号的横坐标,类似于1dt,2dt,3dt,直到(L-1)t
% 这意味着,你的Fs越大,或者T越小,得到的结果越准确。
%*****************************************************************
% 这一段是自己假设一个输入时域信号
f0=10; % 频率值
y1 = sin(2*pi*f0*t); % 时域函数
S = y1; % 原函数
%*****************************************************************
Y = fft(S); % 调用fft(x),不用fft(x,n),据说前者更准确
P2 = abs(Y/L); % 每个量除以数列长度 L
% **********(为什么要除以L?)********
P1 = P2(1:L/2+1); % 取交流部分,这个L/2+1是对的,已经验证过了
P1(2:end-1) = 2*P1(2:end-1); % 交流部分模值乘以2
f = Fs*(0:(L/2))/L; % 计算频域中傅里叶信号实际的频率的横坐标,类似于1df,2df,3df,直到Fs/2
subplot(2,1,1);
plot(t,S) % 原函数作图
subplot(2,1,2);
plot(f,P1) % 傅里叶作图 这个振幅才是真实的振幅,对Y已经乘以2/L了,所以振幅是真实的
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')显示结果:
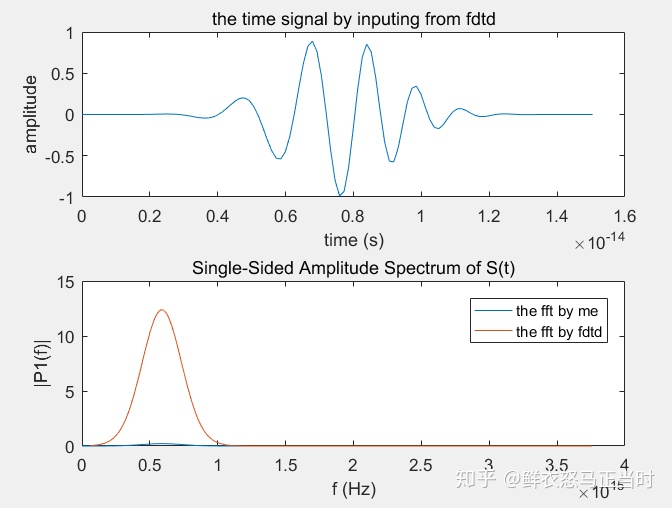
2. 这是在已有一串数据的情况下,想要对这串数据作傅里叶变换。
clear;clc
T = 0.13315e-15; % 采样周期 或者说是时域信号的时间步长
Fs = 1/T; % 采样频率,要大于时域信号中最大频率的两倍
%*****************************************************************
% 这一段是处理从外部文件导入的数据
data1 = xlsread('C:UserssunjieDesktopdata.xlsx','sheet2','A2:B115');
% xlsread()是调用的函数;'C...data.xlsx'是文件路径包含文件名;'sheet1'是表格中的第几个页;'A2:B115'
% 是数据的范围,拉出一个对角线
input = data1(1:114,1:2); % 在上述范围中选择要导入的数据
amplitudes = input(:,2); % 在导入的数据中选择一串要处理的数据,即时域信号振幅离散点
L = length(amplitudes); % 信号长度(原始数据导入的信号点的个数)
%*****************************************************************
t = (0:L-1)*T; % 时间相量,类似于1dt,2dt,3dt
% 据我计算,这个时间步长T必须是所选取的离散点的相邻时间间隔,所以T和Fs在这里是已知且不变的
% 除非你在这串数据中进行插值,让L更长,数据点更多,相当于T更小,Fs更大,所以采样点更多,更准确
S = amplitudes; % 时域信号振幅序列,L个数据点
Y = fft(S); % 调用fft(x)
P2 = abs(Y/L); % 每个量除以数列长度 L
% **********(为什么要除以L?)********
P1 = P2(1:L/2+1); % 取交流部分,这个L/2+1是对的,已经验证过了
P1(2:end-1) = 2*P1(2:end-1); % 交流部分模值乘以2
f = Fs*(0:(L/2))/L; % 傅里叶变换后得到频域的横坐标
%*****************************************************************
% 这个是程序里自己做的傅里叶变换,它已经在上述数据中插值了,所以得到的频域曲线更光滑
data2 = xlsread('C:UserssunjieDesktopdata.xlsx','sheet3','A2:B4034');
input2 = data2(1:4033,1:2);
y2 = input2(:,2);
f2 = 5.86734e13:(-5.86734e13+3.75235e15)/4032:3.75235e15;
%******************************************************************
subplot(2,1,1);
plot(t,S) % 导入的时域信号数据作图
title('the time signal by inputing from fdtd')
xlabel('time (s)')
ylabel('amplitude')
subplot(2,1,2);
plot(f,P1) % 傅里叶变换作图 这个振幅才是真实的振幅,即已乘以L/2
hold on
plot(f2,p2) % 软件的傅里叶变换作图,它没有乘以L/2,所以振幅是相对值
legend('the fft by me','the fft by fdtd');
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')显示结果:
完成啦!
最后
以上就是帅气钥匙最近收集整理的关于matlab中如何编fft函数_Matlab中对时域函数作傅里叶变换 即FFT函数的使用的全部内容,更多相关matlab中如何编fft函数_Matlab中对时域函数作傅里叶变换内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复