FFT的由来

DFT的计算量

因此当N比较大时，计算量太大，所以在快速傅里叶变换出现以前，直接用DFT算法进行谱分析和信号的实时处理是不切实际的

降低运算量的途径

把N点DFT分解为几个较短的DDFT，可使乘法次数大大减少，另外，利用旋转因子$W_N^m$的周期性、对称性和可约性来减少DFT的运算次数
$$W_N^{m+lN}=e^{-j\frac{2\pi }{N}(m+lN)}=e^{-j\frac{2\pi }{N}(m)}<-周期性$$

$$W_N^{-m}=W_N^{N-m},[W_N^{N-m}]\ast =W_N^m,W_N^{m+\frac{N}{2}}=-W_N^m<-对称性$$

$$W_N^m=W_{N/n}^{m/n},N/n,m/n为整数<-可约性$$

基2FFT算法

设序列点数$N=2^L$，L为正整数。若不满足，则补零，使N为2的整数幂的FFT算法称为基-2FFT算法

• 基2时间抽取DIT-FFT
  $$x(n)->\{\begin{array}{l}x(2r)\\ x(2r+1)\end{array}r=0,1,...\frac{N}{2}-1$$

• 基2频域抽取DIF-FFT
  $$X(k)->\{\begin{array}{l}X(2m)\\ X(2m+1)\end{array}m=0,1,...,\frac{N}{2}-1$$

时域抽取基2FFT算法

第一次分解

将序列x(n)按n的奇偶分两组
$$\{\begin{array}{l}x(2r)=x_1(r)\\ x(2r+1)=x_2(r)\end{array}r=0,1,...\frac{N}{2}-1$$
$X(k)=DFT[x(n)]={\sum }_{n=0}^{N-1}x(n)W_N^{nk}={\sum }_{n=even}x(n)W_N^{kn}+{\sum }_{n=odd}x(n)W_N^{kn}$

​ $={\sum }_{r=0}^{\frac{N}{2}-1}x(2r)W_N^{2kr}+{\sum }_{r=0}^{\frac{N}{2}-1}x(2r+1)W_N^{k(2r+1)}$

​ $={\sum }_{r=0}^{\frac{N}{2}-1}{x}_1(r)W_N^{2kr}+W_N^k{\sum }_{r=0}^{\frac{N}{2}-1}{x}_2(r)W_N^{2kr}$

​ $={\sum }_{r=0}^{\frac{N}{2}-1}{x}_1(r)W_{\frac{N}{2}}^{kr}+W_N^k{\sum }_{r=0}^{\frac{N}{2}-1}{x}_2(r)W_{\frac{N}{2}}^{kr}$

因为$X_1(k)={\sum }_{r=0}^{\frac{N}{2}-1}{x}_1(r)W_{\frac{N}{2}}^{kr}=DFT[x_1(r)],X_2(k)={\sum }_{r=0}^{\frac{N}{2}-1}{x}_2(r)W_{\frac{N}{2}}^{kr}=DFT[x_2(r)]$

所以上式$=X_1(k)+W_N^k{X}_2(k),k=0,1,..N/2-1$

$\because X(k)=X_1(k)+W_N^k{X}_2(k),0\le k\le N-1$

上式只是求出$0\le k\le \frac{N}{2}-1$时的X(k)，即前半部分的X(k)，对于$\frac{N}{2}\le k\le N$如何求？

利用周期性求X(k)的后半部分

$\because X_1(k),X_2(k)是以N/2为周期的$

$\therefore X_1(k+\frac{N}{2})=X_1(k),X_2(k+\frac{N}{2})=X_2(k)$

又$W_N^{k+\frac{N}{2}}=W_N^{\frac{N}{2}}{W}_N^k=-W_N^k$，所以后半个序列的求法如下：
$$X(k+N/2)=X_1(k+N/2)+W_N^{k+N/2}{X}_2(k+N/2)=X_1(k)-W_N^k{X}_2(k),0\le k\le \frac{N}{2}-1$$

第二次分解

$X_1(k)={\sum }_{l=0}^{N/4-1}{x}_1(2l)W_{N/2}^{2kl}+{\sum }_{l=0}^{N/4-1}{x}_1(2l+1)W_{N/2}^{k(2l+1)}$

​ $={\sum }_{l=0}^{N/4-1}{x}_3(l)W_{N/4}^{kl}+W_{N/2}^k{\sum }_{l=0}^{N/4-1}{x}_4(l)W_{N/4}^{kl}$

​ $=X_3(k)+W_{N/2}^k{X}_4(k),0\le k\le N/4-1$

$X_1(k)=X_3(k)+W_{N/2}^k{X}_4(k),0\le k\le N/4-1$

$X_1(k+N/4)=X_3(k)-W_{N/2}^k{X}_4(k),0\le k\le N/4-1$

$X_2(k)=X_5(k)+W_{N/2}^k{X}_6(k),0\le k\le N/4-1$

$X_2(k+N/4)=X_5(k)-W_{N/2}^k{X}_6(k),0\le k\le N/4-1$

其中

$x_3(l)=x_1(2l),0\le l\le N/4-1$

$x_4(l)=x_1(2l+1),0\le l\le N/4-1$

$X_3(k)={\sum }_{l=0}^{N/4-1}{x}_3(l)W_{N/4}^{kl}=DFT[x_3(l)]$

$X_4(k)={\sum }_{l=0}^{N/4-1}{x}_4(l)W_{N/4}^{kl}=DFT[x_4(l)]$

$x_5(l)=x_2(2l),0\le l\le N/4-1$

$x_6(l)=x_2(2l+1),0\le l\le N/4-1$

$X_5(k)={\sum }_{l=0}^{N/4-1}{x}_5(l)W_{N/4}^{kl}=DFT[x_5(l)]$

$X_6(k)={\sum }_{l=0}^{N/4-1}{x}_6(l)W_{N/4}^{kl}=DFT[x_6(l)]$

蝶形运算

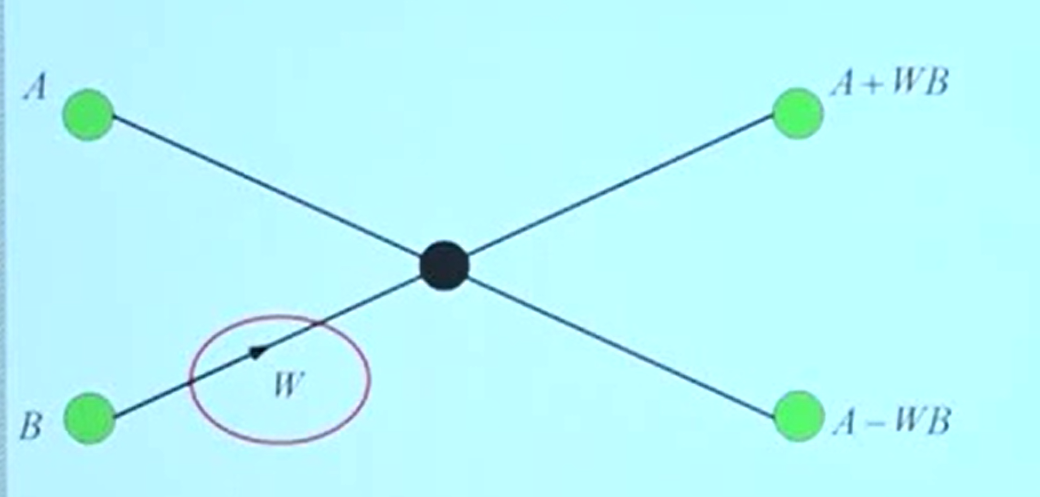
$\Rightarrow$

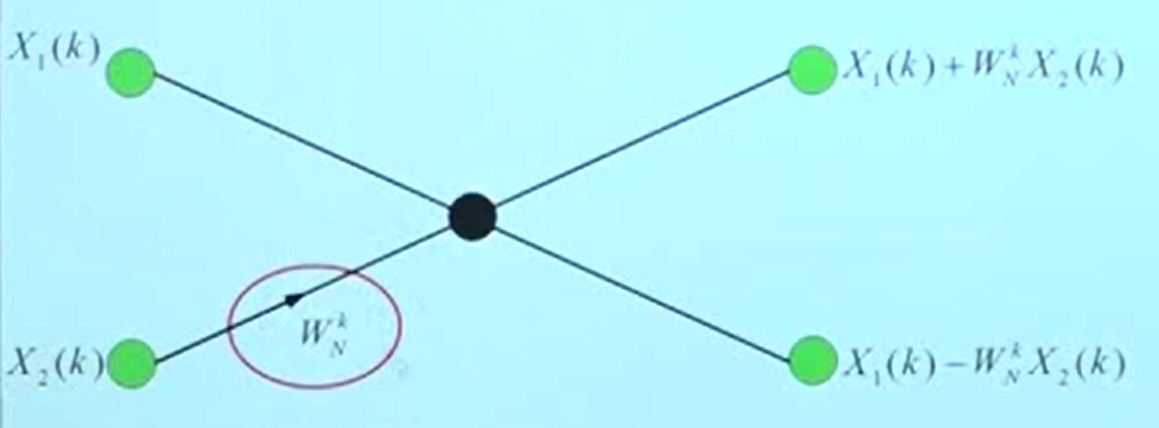
蝶形单元需要一次复数乘法，两次复数加法

利用蝶形运算得到N=8点时的DIT-FFT运算流图

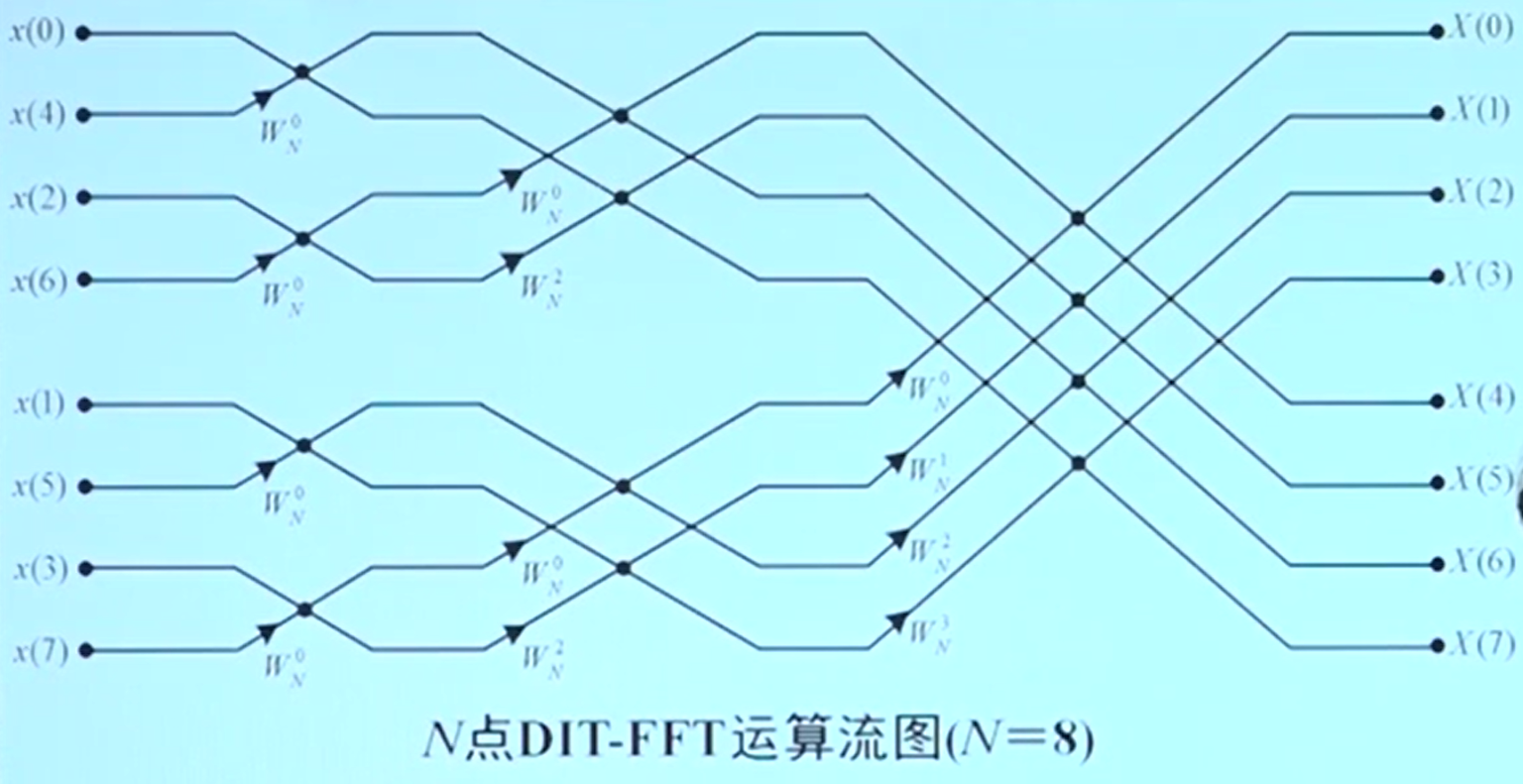
分析：N点DIT-FFT包含

M级蝶形运算，每一级包含N/2个蝶形单元

一个蝶形单元需要一次复数乘法，两次复数加法，因此：

$C_M=M\cdot \frac{N}{2}=\frac{N}{2}lo{g}_{2}N,C_A=M\cdot \frac{N}{2}\times 2=Nlo{g}_{2}N$

DIT-FFT与直接计算DFT运算量比较

直接计算： 需要$N^2$次复数乘法，N(N-1)次复数加法

DIT-FFT$\{\begin{array}{ll}{C}_M=M\cdot \frac{N}{2}=\frac{N}{2}lo{g}_{2}N& 复数乘法\\ C_A=M\cdot \frac{N}{2}\times 2=Nlo{g}_{2}N& 复数加法\end{array}$

加速：$R=\frac{N^2}{(N/2)lo{g}_{2}N}=\frac{2N}{lo{g}_{2}N}$

MATLAB快速傅里叶变换调用格式：$Xk=fft(xn,N)$

频域抽取基2FFT算法

x(n)，$N=2^M$，M为正整数

按序列号n的自然排序将x(n)前后对半分

$X(k)=DFT[x(n)]={\sum }_{n=0}^{N-1}x(n)W_N^{nk}={\sum }_{n=0}^{N/2-1}x(n)W_N^{nk}+{\sum }_{n=N/2}^{N-1}x(n)W_N^{nk}$

​ $={\sum }_{n=0}^{N/2-1}x(n)W_N^{nk}+{\sum }_{n=0}^{N/2-1}x(n+\frac{N}{2})W_N^{k(n+N/2)}$

​ $={\sum }_{n=0}^{N/2-1}[x(n)+W_N^{kN/2}x(n+\frac{N}{2})]W_N^{kn}$

$\because W_N^{kN/2}=e^{-j\frac{2\pi }{N}k\frac{N}{2}}=e^{-jk\pi }=\{\begin{array}{ll}1& k=even(偶数)\\ -1& k=odd(奇数)\end{array}$

$\therefore X(k)=DFT[x(n)]=\{\begin{array}{ll}X(2r)={\sum }_{n=0}^{N/2-1}[x(n)+x(n+\frac{N}{2})]\cdot W_N^{2rn}& k=even\\ X(2r+1)={\sum }_{n=0}^{N/2-1}[x(n)-x(n+\frac{N}{2})]\cdot W_N^n{W}_N^{2rn}& k=odd\end{array}$

令$\{\begin{array}{l}{x}_1(n)=x(n)+x(n+\frac{N}{2})\\ x_2(n)=[x(n)-x(n+\frac{N}{2})]W_N^n\end{array}$
$$\therefore X(k)=DFT[x(n)]=\{\begin{array}{l}DFT[x_1(n)]\\ DFT[x_2(n)]\end{array}=\{\begin{array}{ll}X(2r)={\sum }_{n=0}^{N/2-1}{x}_1(n)\cdot W_N^{2rn}& k=even\\ X(2r+1)={\sum }_{n=0}^{N/2-1}{x}_2(n)\cdot W_N^{2rn}& k=odd\end{array}$$

$$\therefore X(k)=DFT[x(n)]=\{\begin{array}{l}DFT[x_1(n)]\\ DFT[x_2(n)]\end{array}=\{\begin{array}{ll}X(2r)={\sum }_{n=0}^{N/2-1}{x}_1(n)\cdot W_{N/2}^{rn}=X_1(r)& k=even\\ X(2r+1)={\sum }_{n=0}^{N/2-1}{x}_2(n)\cdot W_{N/2}^{rn}=X_2(r)& k=odd\end{array}$$

利用蝶形运算得到N=8点时的DIF-FFT运算流图

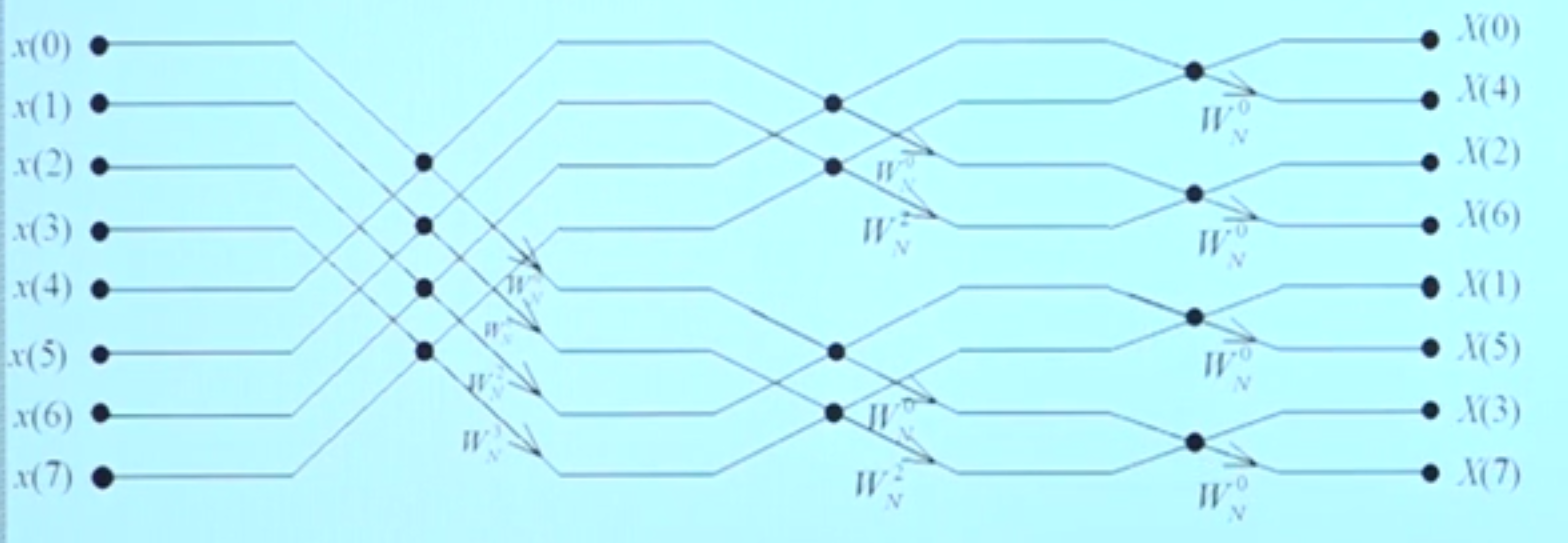
运算量：$C_M=M\cdot \frac{N}{2}=\frac{N}{2}lo{g}_{2}N,C_A=M\cdot \frac{N}{2}\times 2=Nlo{g}_{2}N$

仔细观察基2DIF-FFT运算流图和基2DIT-FFT运算流图会发现，将频域抽取法的运算流图反转，并将输入变输出，输出变输入，正好得到时域抽取法的运算流图

对于实序列进行FFT：把实序列x(n)看作虚部为零的复序列，直接调用fft

IDFT的快速算法

旋转因子指数变极性法

比较DFT和IDFT的运算公式：
$$X(k)=DFT[x(n)]=\sum _{n=0}^{N-1}x(n)e^{-j\frac{2\pi }{N}kn},k=0,1,...,N-1$$

$$x(n)=IDFT[X(k)]=\frac{1}{N}\sum _{k=0}^{N-1}X(k)e^{j\frac{2\pi }{N}kn},n=0,1,...,N-1$$

所以，如果将基2DIT-FFT或基2DIF-FFT算法中的旋转因子$W_N^p$改为$W_N^{-p}$，为X(k)作为输入序列，运算结果乘以1/n，就可以用来快速计算IDFT，得到输出序列x(n)

直接调用FFT子程序：方法1

$x(n)=\frac{1}{N}{\sum }_{k=0}^{N-1}X(k)W_N^{-kn},0\le n\le N-1$

$x^{\ast }(n)=\frac{1}{N}{\sum }_{k=0}^{N-1}{X}^{\ast }(k)W_N^{kn},0\le n\le N-1$

上式两边取共轭得：

x ( n ) = 1 N [ ∑ k = 0 N − 1 X ∗ ( k ) W N k n ] ∗ = 1 N { D F T [ X ∗ ( k ) ] } ∗ , 0 ≤ n ≤ N − 1 x(n)=frac1N[sum_{k=0}^{N-1}X^*(k)W_N^{kn}]^*=frac1N{DFT[X^*(k)]}^*,0leq nleq N-1 x(n)=N1​[∑k=0N−1​X∗(k)WNkn​]∗=N1​{DFT[X∗(k)]}∗,0≤n≤N−1

因此，将X(k)取共轭后得到$X^{\ast }(k)$，输入FFT算出$DFT[X^{\ast }(k)]$，对其取共轭，再乘以1/N得x(n)

直接调用FFT子程序：方法2

X(k)的DFT$g(n)={\sum }_{k=0}^{N-1}X(k)W_N^{kn}=DFT[X(k)],0\le n\le N-1$

根据DFT的时域移位性质得

$\frac{1}{N}g(N-m)=\frac{1}{N}{\sum }_{k=0}^{N-1}X(k)W_N^{k(N-n)}=\frac{1}{N}{\sum }_{k=0}^{N-1}X(k)W_N^{kN}{W}_N^{-kn}$

​ $=\frac{1}{N}{\sum }_{k=0}^{N-1}X(k)W_N^{-kn}=x(n),0\le n\le N-1$

因此，$x(n)=\frac{1}{N}g(N-m),0\le n\le N-1$

将X(k)作为FFT的输入，求出g(n)，将g(n)进行移位的g(N-m)，再乘以1/n，得x(n)，即求出X(k)的逆IDFT

最后

以上就是细腻烧鹅为你收集整理的数字信号处理(五)快速傅里叶变换FFT的由来基2FFT算法IDFT的快速算法的全部内容，希望文章能够帮你解决数字信号处理(五)快速傅里叶变换FFT的由来基2FFT算法IDFT的快速算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。