数字信号处理学习笔记（二）|快速傅里叶变换

快速傅里叶变换(FFT)

一、FFT出现的原因

对x（n）进行N点DFT计算，一共有N² 次乘法，N²次加法
如果N=1024，则有2*1048576次计算，计算量过于庞大。
FFT的思想就是：不断把长序列的DFT分解成几个短序列的DFT，并利用W_N^kn的周期性和对称性来减少DFT的运算次数。

二、DIT-FFT

（1）8点DFT一次时域抽取分解运算

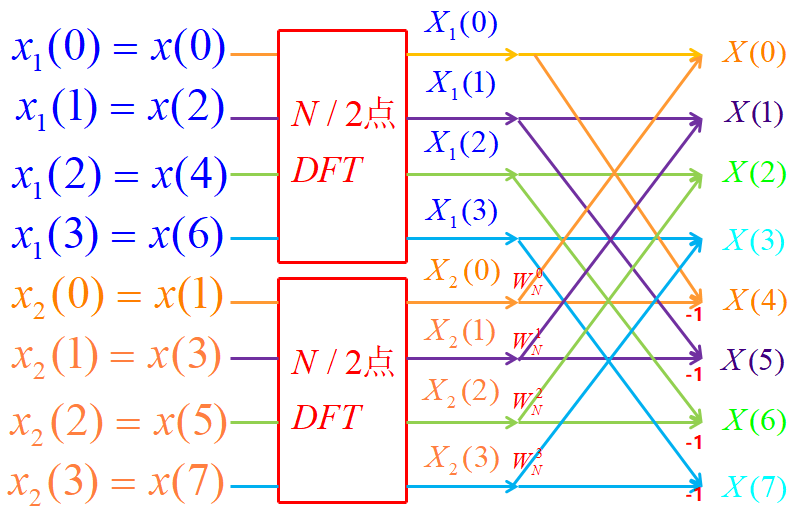
经过一次分解后，计算1个N点DFT共需要计算两个N/2点DFT和N/2个蝶形运算。而计算一个N/2点DFT需要(N/2)²次复数乘法和N/2(N/2-1)次复数加法。仅仅经过一次分解，就使运算量减少近一半。

（2）8点DFT二次时域抽取分解运算

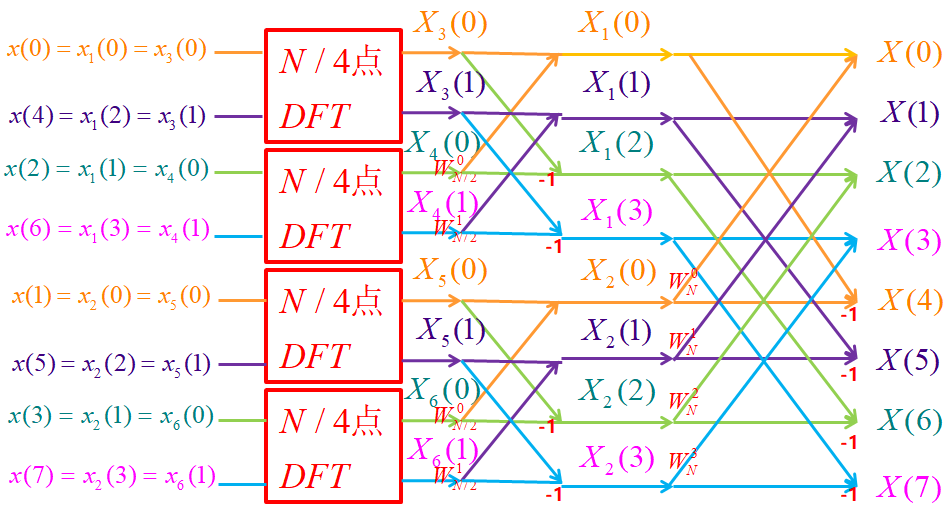
经过第二次分解，又将N/2点DFT分解为2个N/4点DFT和N/4个蝶形运算，而1点DFT就是时域序列本身。

（3）DIT-FFT与DFT运算量的比较

设N=2^M ,有M级蝶形。每一级都由N/2个蝶形运算构成。每一级运算都需要N/2次复数乘和N次复数加

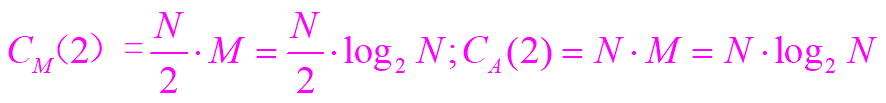
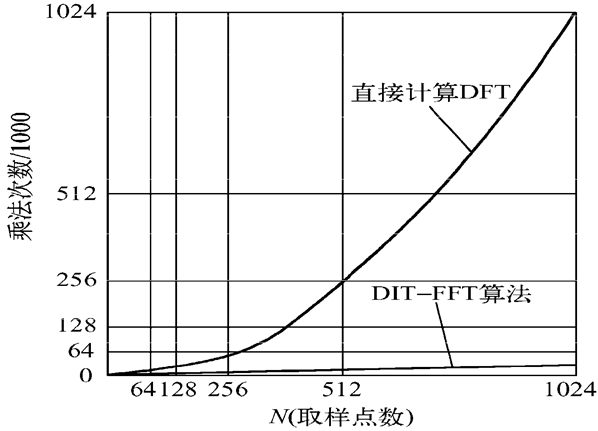
下图显示了DIT-FFT与DFT运算量的比较，可以直观看出FFT算法的优越性。N越大时，优越性就越明显。

三、用Python实现FFT算法

import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 显示负号

# 采样点选择1400个
x = np.linspace(0, 1, 1400)

# 设置需要采样的信号，频率分量有200，400和600
y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin(2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x)

fft_y = fft(y)  # 快速傅里叶变换

N = 1400
x = np.arange(N)  # 频率个数
half_x = x[range(int(N / 2))]  # 取一半区间

abs_y = np.abs(fft_y)  # 取复数的绝对值，即复数的模(双边频谱)
angle_y = np.angle(fft_y)  # 取复数的角度
normalization_y = abs_y / N  # 归一化处理（双边频谱）
normalization_half_y = normalization_y[range(int(N / 2))]  # 由于对称性，只取一半区间（单边频谱）

plt.subplot(411)
plt.plot(x[0:50],y[0:50])
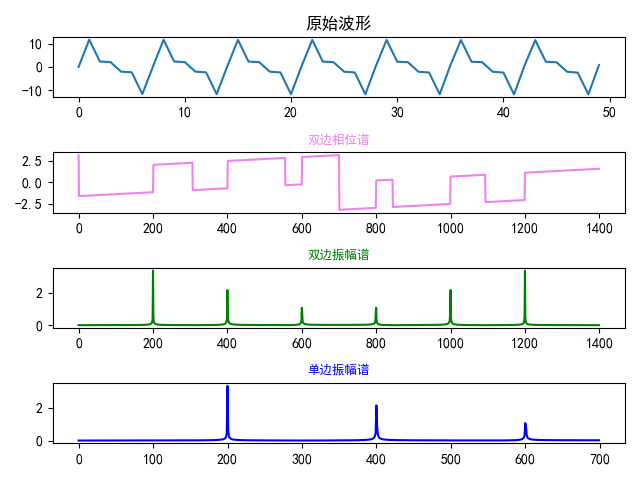
plt.title('原始波形')

plt.subplot(412)
plt.plot(x, angle_y, 'violet')
plt.title('双边相位谱', fontsize=9, color='violet')

plt.subplot(413)
plt.plot(x, normalization_y, 'g')
plt.title('双边振幅谱', fontsize=9, color='green')

plt.subplot(414)
plt.plot(half_x, normalization_half_y, 'blue')
plt.title('单边振幅谱', fontsize=9, color='blue')

plt.show()

最后

以上就是传统短靴为你收集整理的数字信号处理学习笔记（二）|快速傅里叶变换的全部内容，希望文章能够帮你解决数字信号处理学习笔记（二）|快速傅里叶变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。