尝试回答下面问题：

双线性函数基础
1.什么是双线性函数？
2.举一个双线性函数的例子（除了最简单向量内积）
3.什么是双线性函数的度量矩阵？
4.写出一个你所举例子中的度量矩阵
5.用过渡矩阵对所选的基进行变换后，度量矩阵会发生怎样的变化？

对称双线性函数基础
1.什么是对称双线性函数，什么是反对称双线性函数？
2.对称双线性函数的度量矩阵是对称矩阵吗？如何证明？
3.是否有“若$f$为$\mathbb{C}$上的对称双线性函数且$f(\xi ,\xi )=0$，则$\xi =0$”？
4.是否有“如果$f(\alpha ,\beta )$是定义在复数域线性空间上维数>1的对称双线性函数，则有线性无关的向量$\xi ,\eta$使得$f(\xi ,\eta )=1,f(\xi ,\xi )=f(\eta ,\eta )=0$”？简述理由

反对称双线性函数基础
1.反对称双线性函数的度量矩阵是反对称矩阵吗？如何证明？
2.反称双线性函数的充要条件是$\forall \alpha \in V$都有$f(\alpha ,\alpha )=0$（北大第四P418 T13）

双线性函数基础和度量矩阵

什么是双线性函数？

$f(\alpha ,k_1{\beta }_1+k_2{\beta }_2)=k_{1}f(\alpha ,{\beta }_1)+k_{2}f(\alpha ,{\beta }_2)$
$f(k_1{\alpha }_1+k_2{\alpha }_2,\beta )=k_{1}f({\alpha }_1,\beta )+k_{2}f({\alpha }_2,\beta )$

能否举一个具体的双线性函数的例子（除了最简单向量内积）

$f(X,Y)=Tr(X^{\prime }AY)$，其中$X,Y\in P^{m\times n},A\in P^{m\times m}$。验证它是双线性函数，只需$f(X,k_{1}Y+k_{2}Y)=Tr(X^{\prime }A(k_1{Y}_1+k_2{Y}_2))=k_{1}Tr(X^{\prime }A{Y}_1)+k_{2}Tr(X^{\prime }A{Y}_2)$即可
这使用了迹的线性性质，这个双线性函数在欧几里得空间中是内积，且定义了名为Frobenuis的范数

什么是双线性函数的度量矩阵？

给出$f(\alpha ,\beta )$中$\alpha$和$\beta$所在空间V的一组基${ϵ}_1,...,{ϵ}_n$，度量矩阵为$(f({ϵ}_i,{ϵ}_j){)}_{n\times n}$

能否写出一个你所举例子中的度量矩阵？（北大第四P417 T10）

• 先给出$P^{m\times n}$的一组基：$E_{1,1},E_{1,2},...,E_{m,n}$，其中$E_{i,j}$表示只有第i行第j列元素为1，其余元素为0
• 先计算度量矩阵左上角的元素，计算Cannot read properties of undefined (reading 'type')
• 计算Cannot read properties of undefined (reading 'type')
• 计算Cannot read properties of undefined (reading 'type')
• 根据上述一般结果写出矩阵即可。(附上草稿纸)
  

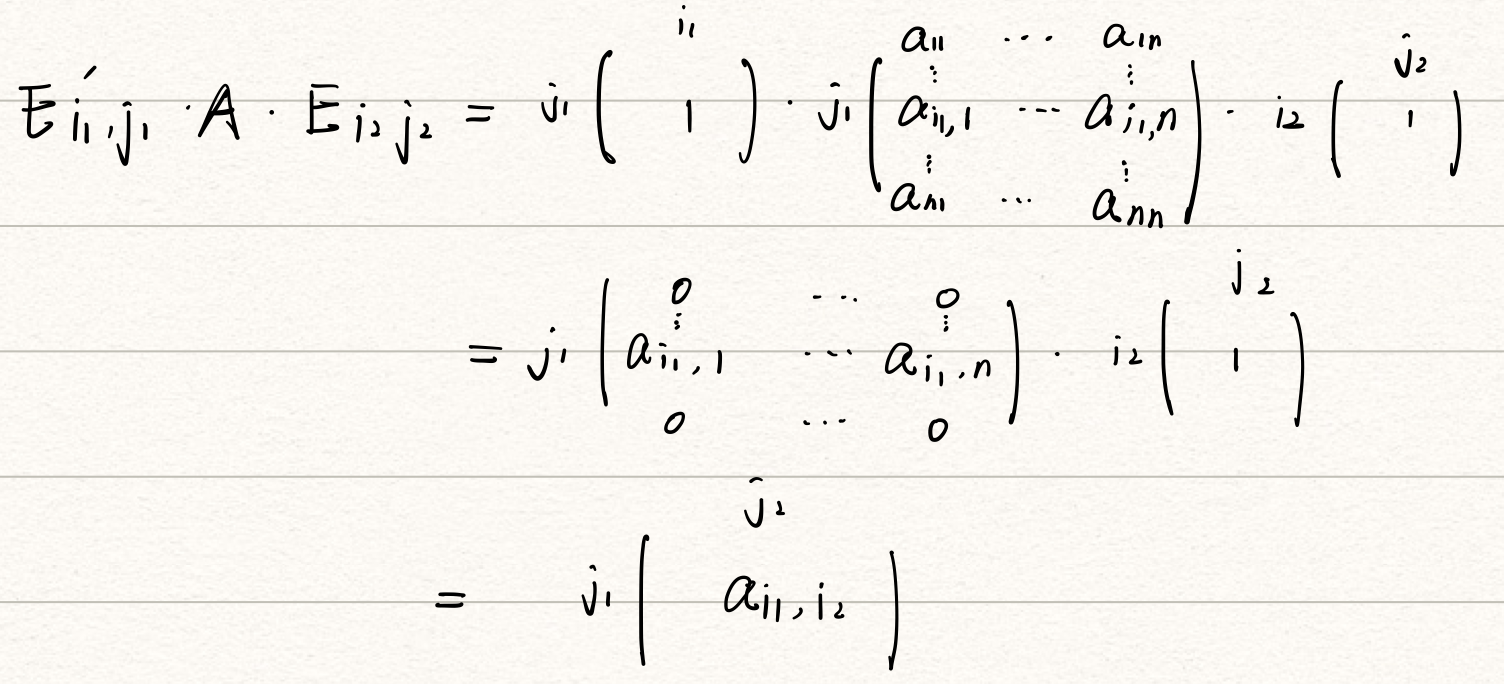
用过渡矩阵对所选的基进行变换后，度量矩阵会发生怎样的变化？

“新基等于旧基度，新矩等于逆旧矩"这与内积的度量矩阵性质相同

对称双线性函数基础

什么是对称双线性函数，什么是反对称双线性函数？

对称双线性：$f(\alpha ,\beta )=f(\beta ,\alpha )$
反对称双线性：$f(\alpha ,\beta )=-f(\beta ,\alpha )$

对称双线性函数的度量矩阵是对称矩阵吗？如何证明？

任意一组基下，对称双线性函数的度量矩阵正定。思路如下：

因为$\forall \alpha ,\beta \in V,f(\alpha ,\beta )=X^{\prime }AY=\sum _{i,j}{a}_{ij}{x}_i{y}_j=f(\beta ,\alpha )=Y^{\prime }AX=\sum _{i,j}{a}_{ij}{y}_i{x}_j$，根据对称双线性定义+二次型性质选取$X={ϵ}_i,Y={ϵ}_j$，则有$a_{ij}=a_{ji}$，证毕。

是否有“若$f$为$\mathbb{C}$上的对称双线性函数且$f(\xi ,\xi )=0$，则$\xi =0$”？简述理由。（北大第四P418 T12）

不一定成立。// 这是定义在欧几里得空间中内积的正定性（欧几里得空间定义在$\mathbb{R}$），这里不一定成立

• 理由：可以选择一组基，使得$f$在这组基下的度量矩阵为Cannot read properties of undefined (reading 'type')的形式，其中$r$为度量矩阵的秩
  如果n=r=1，此时原命题成立，因为$f(\alpha ,\alpha )=(x_1{)}^{\prime }\cdot E_1\cdot (x_1)=x_1^2\ge 0$，
  如果$n\ge 2$，此时原命题不成立，原因：
  • 当$n>r$时我们可以找到一个$\xi$的坐标为$(\underset{r个零}{\underbrace{0,...,0}},\underset{n-r个1}{\underbrace{1,...,1}}{)}^{\prime }$使得$f(\xi ,\xi )={\xi }^{\prime }A\xi =0$，
    当$n=r$时，我们可以找到一个$\xi$的坐标为$(1,i,0...,0{)}^{\prime }$使得$f(\xi ,\xi )=0$

是否有“如果$f(\alpha ,\beta )$是定义在复数域线性空间上维数>1的对称双线性函数，则有线性无关的向量$\xi ,\eta$使得$f(\xi ,\eta )=1,f(\xi ,\xi )=f(\eta ,\eta )=0$”？简述理由

成立。可以使用构造法证明

取$\xi =(\frac{1}{\sqrt{2}},\frac{i}{\sqrt{2}},0,\cdots ,0)$，这使得$f(\xi ,\xi )=(\frac{1}{\sqrt{2}},\frac{i}{\sqrt{2}},0,\cdots ,0{)}^{\prime }{E}_r(\frac{1}{\sqrt{2}},\frac{i}{\sqrt{2}},0,\cdots ,0)=0$（f作为对称双线性函数，在上一题所选定的基下，度量矩阵为$E_r$）
取$\eta =(\frac{1}{\sqrt{2}},\frac{-i}{\sqrt{2}},0,...,0)$，这使得$f(\eta ,\eta )=0$，且$f(\xi ,\eta )=1$

反对称双线性函数基础

反对称双线性函数的度量矩阵是反对称矩阵吗？如何证明？

任意一组基下，反对称双线性函数的度量矩阵正定。思路同对称双线性函数

反称双线性函数的充要条件是$\forall \alpha \in V$都有$f(\alpha ,\alpha )=0$（北大第四P418 T13）

• 必要性：提示:能否写出反称双线性函数的定义？

• 充分性：由于$f(\alpha ,\alpha )=0$对于任意$\alpha$成立，故$\forall \beta \in V,f(\alpha +\beta ,\alpha +\beta )=0=f(\alpha ,\alpha )+f(\alpha ,\beta )+f(\beta ,\alpha )+f(\beta ,\beta )=f(\alpha ,\beta )+f(\beta ,\alpha )=0$，所以反称。

最后

以上就是心灵美星月最近收集整理的关于双线性函数基础尝试回答下面问题：双线性函数基础和度量矩阵对称双线性函数基础反对称双线性函数基础的全部内容，更多相关双线性函数基础尝试回答下面问题内容请搜索靠谱客的其他文章。