BSV 上的双线性配对

基于配对的密码学是椭圆曲线密码学的一种变体。由于配对的特点，新的密码算法和协议可以实现传统密码学无法实现的功能或效率，例如基于身份的加密（IBE）、基于属性的加密（ABE）、认证密钥交换（AKE）和短签名。

基于配对的密码学的几种应用已在许多区块链中得到实际应用。

• Zcash 实现了自己的零知识证明算法，名为 zk-SNARKs（零知识简洁非交互式知识论证）
• 以太坊支持配对检查以执行 zkSNARK 验证
• DFINITY（现在称为互联网计算机）构建了一个基于 BLS 签名的方案，比 ECDSA 签名更短。

我们将展示配对可以直接在 BSV 上实现，从而使以前认为不可能在 BSV 上实现的各种基于配对的密码学应用成为可能。

双线性配对

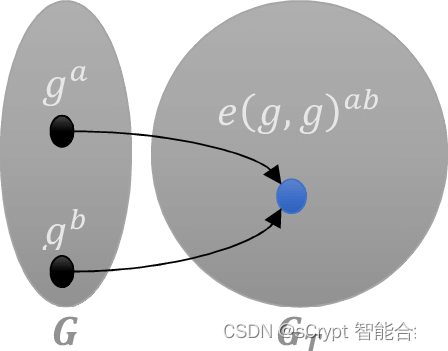
配对 e 只是一个函数，它接受两个输入¹ 并返回一个输出，如下所示。

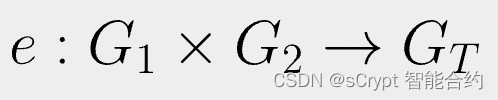
双线性配对具有以下性质：

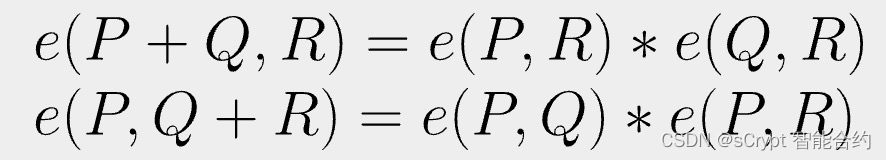
也就是说，它在每个输入中都是线性的。很容易看到以下成立。

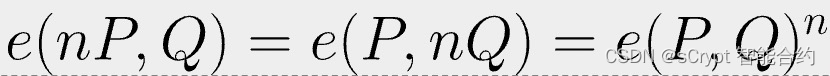
直观地说，可以在其输入之间交换标量 n 并将其作为指数取出。

示例

让我们看看下面的配对函数。

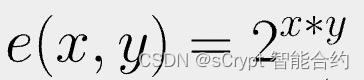
它是双线性的，因为它满足上面的两个方程。例如，

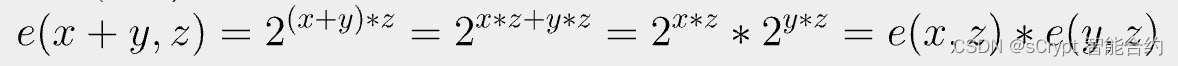
椭圆曲线上的双线性配对

实际上，上述配对对于加密使用来说并不安全。相反，我们使用椭圆曲线上的配对。输入是椭圆曲线上的点，输出是数字²。有多种方法可以在椭圆曲线上构建配对，例如 Weil 配对、Tate 配对 和 Ate 配对。

米勒算法

米勒算法 (Miller’s algorithm) 用于有效地计算配对。它由两部分组成：

1. 主循环：第 3 行到第 10 行。在计算标量点乘法时，它在结构上类似于双加算法。
2. 第 11 行的最终求幂。

p、k 和 r 是椭圆曲线所用的参数³。

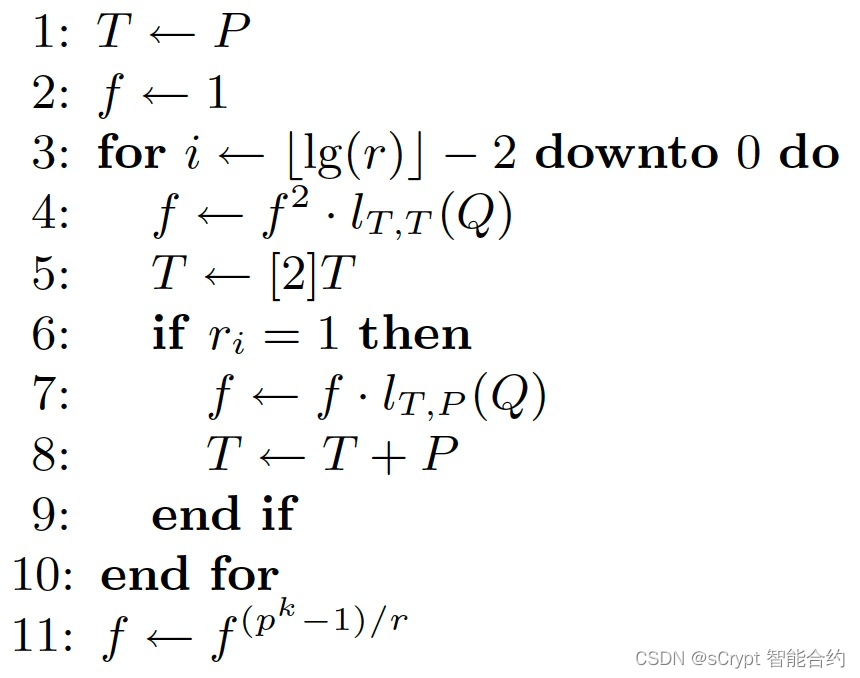
实现

我们已经实现了米勒算法来计算下面的Tate配对，基于我们的椭圆曲线算术库。

static function millerLoop(Point P, Point Q): int {
    Point T = P;
    int f = 1;

    // main miller loop
    loop (N) : i {
        f = f * f * linefunc(T, T, Q);
        T = EC.doublePoint(T);

        int j = N - 1 - i;
        if (r & (mask << j)) {
            f = f * linefunc(T, P, Q);
            T = EC.addPoints(T, P);
        }
    }
    return f;
}

// compute the pairing e(P, Q)
static function pairing(Point P, Point Q): int {
    int f = millerLoop(P, Q);
    // final exponentiation
    return pow(f, EXP);
}

linefunc(P, Q, R) 是一个通过 P 和 Q 并在 R 处求值的线性函数。

[1] 因而称为配对。

[2] 严格来说，它是乘法群中的一个元素。由于这是对配对的介绍，因此我们在整篇文章中选择可读性而不是数学严谨性。

[3] 并非所有椭圆曲线都可以用于配对。在实践中只使用那些能够高效计算的配对的曲线。它们被称为配对友好曲线，其中 Barreto-Naehrig (BN) 或 Boneh-Lynn-Shacham (BLS) 曲线是值得注意的例子。

最后

以上就是有魅力酒窝为你收集整理的BSV 上的双线性配对的全部内容，希望文章能够帮你解决BSV 上的双线性配对所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。