einsum函数
einsum函数在文档中的解释为:

即,该函数提供了一种使用爱因斯坦求和约定来计算多线性表达式的方法(即乘积和)
爱因斯坦求和约定(Einstein summation convention)
关于爱因斯坦求和约定的详细运算过程参考知乎大佬的回答:https://zhuanlan.zhihu.com/p/46006162以及B站up的视频:https://www.bilibili.com/video/BV1ot411V71V?from=search&seid=9196910873956345075
百度百科对爱因斯坦求和约定的表述如下:
所谓Einstein约定求和就是略去求和式中的求和号。在此规则中两个相同指标就表示求和,而不管指标是什么字母,有时亦称求和的指标为“哑指标”。
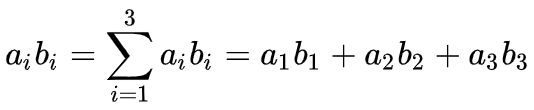
具体约定如下:
1、在同一项中,如果同一指标(如上式中的i)成对出现,就表示遍历其取值范围求和。这时求和符号可以省略,如上所示。
2、上述成对出现的指标叫做哑指标,简称哑标。表示哑标的小写字母可以用另一对小写字母替换,只要其取值范围不变。
3、当两个求和式相乘时,两个求和式的哑标不能使用相同的小写字母。为了避免混乱,常用的办法是根据上一条规则,先将其中一个求和式的哑标改换成其它小写字母。(这一条规则以后会用到)
其实上述描述,只是为了帮助我们接受这种标记维度的思想,在代码中并不会有很复杂的理论推导过程。
einsum语法
einsum(equation, operands)
其中equation即为维度约定。其表示方式如下例:
“i, j ->ij”
其中,i, j 标记两个操作数的维度,ij为输出结果的维度标记。
完整指令为einsun(“i, j -> ij”, a, b),指令实现的效果为:两个一维向量的维度分别被标记为i, j,这两个向量在函数内经过乘积加和操作,最终输出一个二维矩阵,其维度标记为ij。
下面是文档中的示例:
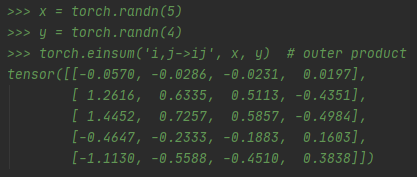
生成两个一维向量,长度分别为5, 4.
在函数中分别将两个向量的维度标记为i,j并给定输出结果的维度标记为ij,即为54
然后将操作数a,b传入函数,即可得到想要的结果。
此过程进行的是矩阵乘法操作。
示例2:

这里分别生成了一个三维数组和两个二维数组。
标记规则为“bn, anm, bm -> ba",即表示操作数的维度分别被标记为bn, anm, bm,它们对应的数值为25, 354,24它们对应的数组为l, A, r。最终输出结果的维度标记为ba,即最后要生成一个二维数组,且数组的尺寸为23。
此过程相当于对输入操作数进行一次双线性变换。
pytorch中双线性变换指令表述如下:
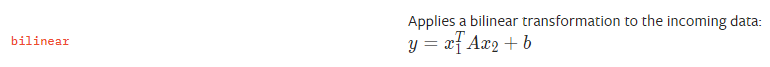
示例3:
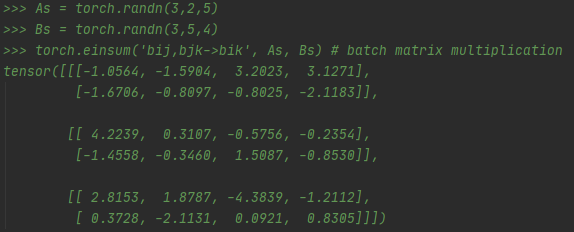
操作数为两个三维数组,尺寸分别为325, 354,对应标记为:bij, bjk,输出维度标记为bik即尺寸为324.
这个操作就是批次矩阵间乘法(我自己起的名字o_o)。具体可以解释为:两个数组,第一个数组是3个25矩阵的集合,第二个数组是3个5*4的矩阵集合,这两个数组相乘,就是两个矩阵的集合中对应位置上的二维矩阵做矩阵乘法,得到的结果再组成一个新的二维矩阵的集合。
示例4:
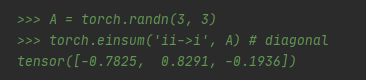
这个操作为取对角线元素。
示例5:
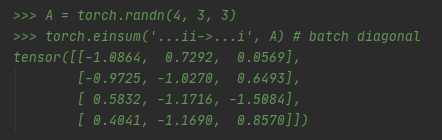
这个操作可以看做是取二维方阵的集合中每个二维方阵的对角线元素组成新的数组。
示例6:

这个就是改变维度排列顺序的操作。使用省略号就是指不管前边有几个维度,只对给定的最后两个维度做交换操作。
其他操作
下面还要借用知乎大佬的回答:https://zhuanlan.zhihu.com/p/101157166
总结了一些其他操作。
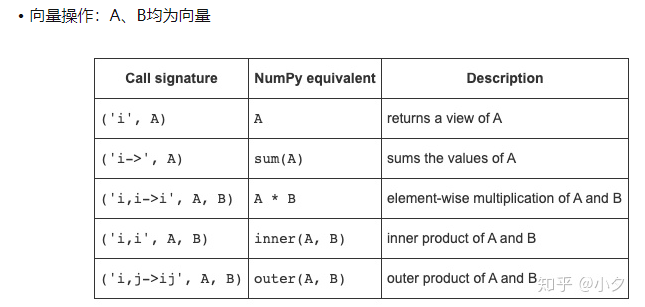
向量操作:A、B均为2D矩阵
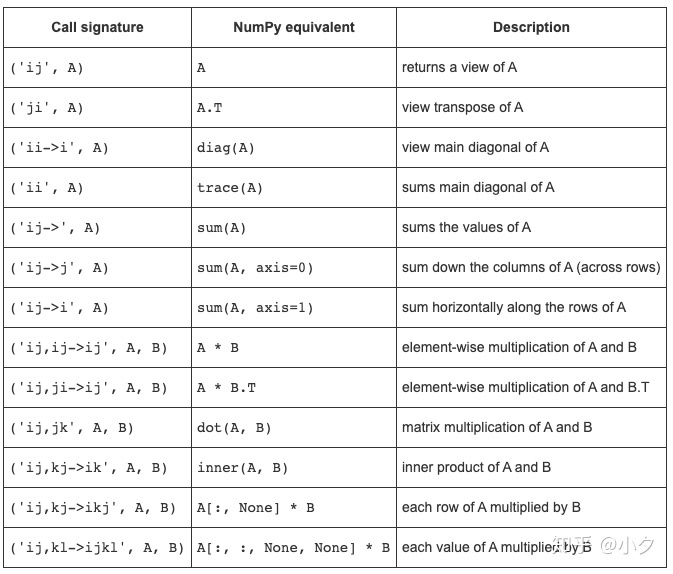
最后
以上就是典雅自行车最近收集整理的关于pytorch中的einsum函数einsum函数的全部内容,更多相关pytorch中内容请搜索靠谱客的其他文章。








发表评论 取消回复