1.爱因斯坦求和约定

PyTorch/TensorFlow中那些计算点积、外积、转置、矩阵-向量乘法、矩阵-矩阵乘法的函数名字和签名很费劲，那么einsum记法就是我们的救星。einsum记法是一个表达以上这些运算，包括复杂张量运算在内的优雅方式，基本上，可以把einsum看成一种领域特定语言。一旦你理解并能利用einsum，除了不用记忆和频繁查找特定库函数这个好处以外，你还能够更迅速地编写更加紧凑、高效的代码。而不使用einsum的时候，容易出现引入不必要的张量变形或转置运算，以及可以省略的中间张量的现象。此外，einsum这样的领域特定语言有时可以编译到高性能代码，事实上，PyTorch最近引入的能够自动生成GPU代码并为特定输入尺寸自动调整代码的张量理解（Tensor Comprehensions）就基于类似einsum的领域特定语言。此外，可以使用opt einsum和tf einsum opt这样的项目优化einsum表达式的构造顺序。

比方说，我们想要将两个矩阵和相乘，接着计算每列的和，最终得到向量。使用爱因斯坦求和约定，这可以表达为：

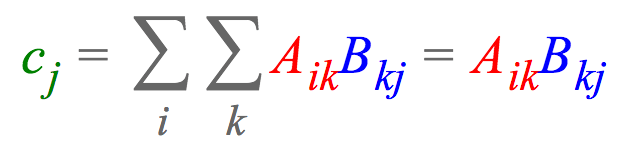
这一表达式指明了中的每个元素是如何计算的，列向量乘以行向量，然后求和。注意，在爱因斯坦求和约定中，我们省略了求和符号Sigma，因为我们隐式地累加重复的下标（这里是k）和输出中未指明的下标（这里是i）。当然，einsum也能表达更基本的运算。比如，计算两个向量a的点积可以表达为：

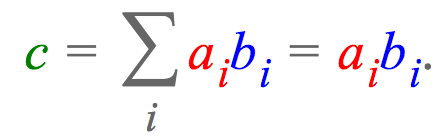
在深度学习中，我经常碰到的一个问题是，变换高阶张量到向量。例如，我可能有一个张量，其中包含一个batch中的个训练样本，每个样本是一个长度为T的K维词向量序列，我想把词向量投影到一个不同的维度Q。如果将这个张量记作，将投影矩阵记作，那么所需计算可以用einsum表达为：

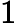
最后一个例子，比方说有一个四阶张量，我们想要使用之前的投影矩阵将第三维投影至维，并累加第二维，然后转置结果中的第一维和最后一维，最终得到张量。einsum可以非常简洁地表达这一切：

注意，我们通过交换下标和（而不是），转置了张量构造结果。

2.以Tf为例

tf.einsum
einsum( equation, *inputs) 
一般来说, 方程是从较熟悉的元素方程得到：

删除变量名称、括号和逗号； 
用 “*” 替换 “，”； 
删除总和标志； 
将输出移到右侧，并将 “=” 替换为 “->>”。 
许多常见操作可以用这种方式来表示。例如:

# Matrix multiplication
>>> einsum('ij,jk->ik', m0, m1)  # output[i,k] = sum_j m0[i,j] * m1[j, k]

# Dot product
>>> einsum('i,i->', u, v)  # output = sum_i u[i]*v[i]

# Outer product
>>> einsum('i,j->ij', u, v)  # output[i,j] = u[i]*v[j]

# Transpose
>>> einsum('ij->ji', m)  # output[j,i] = m[i,j]

# Batch matrix multiplication
>>> einsum('aij,ajk->aik', s, t)  # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]

例子

# 初始化矩阵
x = tf.constant([[1., 2., 3.],
                 [1., 2., 3.]])
y = tf.constant([[2., 3., 4.],
                 [2., 3., 4.]])
z = tf.constant([[3., 4.],
                 [3., 4.],
                 [3., 4.]])
# 外积
out = tf.multiply(x, y)
out1 = tf.einsum('ij,ij->ij', x, y)
# 点积
dot = tf.matmul(x, z)
dot1 = tf.einsum('ij,jk->ik', x, z)
# 转置
trans = tf.transpose(x, [1, 0])
trans1 = tf.einsum('ij->ji', x)
with tf.Session() as sess:
    print('外积')
    print('outn{}'.format(sess.run(out)))
    print('out1n{}'.format(sess.run(out1)))
    print('点积')
    print('dotn{}'.format(sess.run(dot)))
    print('dot1n{}'.format(sess.run(dot1)))
    print('转置')
    print('transn{}'.format(sess.run(trans)))
    print('trans1n{}'.format(sess.run(trans1)))

输出
 

# 初始化矩阵
x = tf.constant([[1., 2., 3.],
                 [1., 2., 3.]])
y = tf.constant([[2., 3., 4.],
                 [2., 3., 4.]])
z = tf.constant([[3., 4.],
                 [3., 4.],
                 [3., 4.]])
# 外积
out = tf.multiply(x, y)
out1 = tf.einsum('ij,ij->ij', x, y)
# 点积
dot = tf.matmul(x, z)
dot1 = tf.einsum('ij,jk->ik', x, z)
# 转置
trans = tf.transpose(x, [1, 0])
trans1 = tf.einsum('ij->ji', x)
with tf.Session() as sess:
    print('外积')
    print('outn{}'.format(sess.run(out)))
    print('out1n{}'.format(sess.run(out1)))
    print('点积')
    print('dotn{}'.format(sess.run(dot)))
    print('dot1n{}'.format(sess.run(dot1)))
    print('转置')
    print('transn{}'.format(sess.run(trans)))
    print('trans1n{}'.format(sess.run(trans1)))

最后

以上就是舒心音响为你收集整理的einsum:深度学习中的爱因斯坦求和约定1.爱因斯坦求和约定2.以Tf为例的全部内容，希望文章能够帮你解决einsum:深度学习中的爱因斯坦求和约定1.爱因斯坦求和约定2.以Tf为例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。