文章目录
- 简介
- 简单函数
- 矢量化数组运算
- 条件逻辑表达式
- 统计方法
- 布尔数组
- 排序
- 文件
- 线性代数
- 随机数
简介
在NumPy中,多维数组除了基本的算数运算之外,还内置了一些非常有用的函数,可以加快我们的科学计算的速度。
简单函数
我们先看下比较常见的运算函数,在使用之前,我们先构造一个数组:
arr = np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
计算数组中元素的开方:
np.sqrt(arr)
array([0. , 1. , 1.4142, 1.7321, 2. , 2.2361, 2.4495, 2.6458,
2.8284, 3. ])
自然常数e为底的指数函数:
np.exp(arr)
array([ 1. , 2.7183, 7.3891, 20.0855, 54.5982, 148.4132,
403.4288, 1096.6332, 2980.958 , 8103.0839])
取两个数组的最大值,组成新的数组:
x = np.random.randn(8)
y = np.random.randn(8)
x,y
(array([-2.3594, -0.1995, -1.542 , -0.9707, -1.307 , 0.2863, 0.378 ,
-0.7539]),
array([ 0.3313, 1.3497, 0.0699, 0.2467, -0.0119, 1.0048, 1.3272,
-0.9193]))
np.maximum(x, y)
array([ 0.3313, 1.3497, 0.0699, 0.2467, -0.0119, 1.0048, 1.3272,
-0.7539])
返 回浮点数数组的小数和整数部分:
arr = np.random.randn(7) * 5
array([-7.7455, 0.1109, 3.7918, -3.3026, 4.3129, -0.0502, 0.25 ])
remainder, whole_part = np.modf(arr)
(array([-0.7455, 0.1109, 0.7918, -0.3026, 0.3129, -0.0502, 0.25 ]),
array([-7., 0., 3., -3., 4., -0., 0.]))
矢量化数组运算
如果要进行数组之间的运算,常用的方法就是进行循环遍历,但是这样的效率会比较低。所以Numpy提供了数组之间的数据处理的方法。
先来讲解一下 np.meshgrid 这个函数,这个函数是用来快速生成网格点坐标矩阵的。
先看一段坐标点的代码:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[0, 1, 2], [0, 1, 2]])
y = np.array([[0, 0, 0], [1, 1, 1]])
plt.plot(x, y,
color='green',
marker='.',
linestyle='')
plt.grid(True)
plt.show()
上面的X是一个二维数组,表示的是坐标点的X轴的位置。
Y也是一个二维数组,表示的是坐标点的Y轴的位置。
看下画出来的图像:
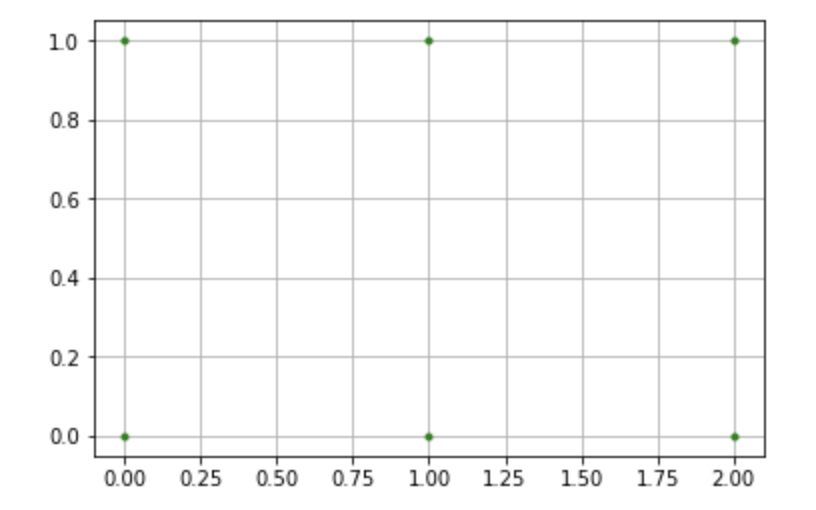
上面画出的就是使用X,Y矩阵组合出来的6个坐标点。
上面的X,Y的二维数组是我们手动输入的,如果坐标上面有大量点的话,手动输入肯定是不可取的。
于是有了np.meshgrid这个函数。这个函数可以接受两个一维的数组,然后生成二维的X,Y坐标矩阵。
上面的例子可以改写为:
x = np.array([0,1,2])
y = np.array([0,1])
xs, ys = np.meshgrid(x, y)
xs,ys
(array([[0, 1, 2],
[0, 1, 2]]),
array([[0, 0, 0],
[1, 1, 1]]))
可以看到生成的xs和ys和手动输入是一样的。
有了网格坐标之后,我们就可以基于网格值来计算一些数据,比如: s q r t ( x 2 + y 2 ) sqrt(x^2+y^2) sqrt(x2+y2) ,我们不用变量矩阵中所有的数据,只需要直接使用数组进行运算即可:
np.sqrt(xs ** 2 + ys ** 2)
结果:
array([[0. , 1. , 2. ],
[1. , 1.41421356, 2.23606798]])
因为xs 和ys本身就是2 * 3 的矩阵,所以结果也是 2 * 3 的矩阵。
条件逻辑表达式
我们可以在构建数组的时候使用条件逻辑表达式:
xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])
result = [(x if c else y)
for x, y, c in zip(xarr, yarr, cond)]
result
[1.1, 2.2, 1.3, 1.4, 2.5]
更简单一点,我们可以使用where语句:
result = np.where(cond, xarr, yarr)
result
array([1.1, 2.2, 1.3, 1.4, 2.5])
我们还可以根据where的条件来修改数组的值:
arr = np.random.randn(4, 4)
arr
array([[ 0.7953, 0.1181, -0.7485, 0.585 ],
[ 0.1527, -1.5657, -0.5625, -0.0327],
[-0.929 , -0.4826, -0.0363, 1.0954],
[ 0.9809, -0.5895, 1.5817, -0.5287]])
上面我们构建了一个4 * 4 的数组。
我们可以在where中进行数据的比较,如果大于0,将数据修改成2 ,如果小于0,则将数据修该成-2 :
np.where(arr > 0, 2, -2)
array([[ 2, 2, -2, 2],
[ 2, -2, -2, -2],
[-2, -2, -2, 2],
[ 2, -2, 2, -2]])
统计方法
numpy提供了mean,sum等统计方法:
arr = np.random.randn(5, 4)
arr
arr.mean()
np.mean(arr)
arr.sum()
还可以按维度来统计:
arr.mean(axis=1)
arr.sum(axis=0)
cumsum进行累加计算:
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7])
arr.cumsum()
array([ 0, 1, 3, 6, 10, 15, 21, 28])
cumprod进行累乘计算:
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
arr
arr.cumsum(axis=0)
array([[ 0, 1, 2],
[ 3, 5, 7],
[ 9, 12, 15]])
arr.cumprod(axis=1)
array([[ 0, 0, 0],
[ 3, 12, 60],
[ 6, 42, 336]])
布尔数组
any用于测试数组中是否存在一个或多个True,而all则检查数组中所有值是否都是True:
bools = np.array([False, False, True, False])
bools.any()
True
bools.all()
False
排序
使用sort可以对数组进行排序,除了普通排序还可以按照特定的轴来进行排序:
arr = np.random.randn(6)
arr.sort()
array([-2.5579, -1.2943, -0.2972, -0.1516, 0.0765, 0.1608])
arr = np.random.randn(5, 3)
arr
arr.sort(1)
arr
array([[-0.8852, -0.4936, -0.1875],
[-0.3507, -0.1154, 0.0447],
[-1.1512, -0.8978, 0.8909],
[-2.6123, -0.8671, 1.1413],
[-0.437 , 0.3475, 0.3836]])
sort(1)指的是按照第二个轴来排序。
文件
可以方便的将数组写入到文件和从文件中读出:
arr = np.arange(10)
np.save('some_array', arr)
会将数组存放到some_array.npy文件中,我们可以这样读取:
np.load('some_array.npy')
还可以以无压缩的方式存入多个数组:
np.savez('array_archive.npz', a=arr, b=arr)
读取:
arch = np.load('array_archive.npz')
arch['b']
如果想要压缩,可以这样:
np.savez_compressed('arrays_compressed.npz', a=arr, b=arr)
线性代数
如果我们使用普通的算数符来进行矩阵的运算的话,只是简单的数组中对应的元素的算数运算。如果我们想做矩阵之间的乘法的时候,可以使用dot。
一个 2 * 3 的矩阵 dot 一个3*2 的矩阵,最终得到一个2 * 2 的矩阵。
x = np.array([[1., 2., 3.], [4., 5., 6.]])
y = np.array([[6., 23.], [-1, 7], [8, 9]])
x
y
x.dot(y)
array([[ 28., 64.],
[ 67., 181.]])
或者可以这样写:
np.dot(x, y)
array([[ 28., 64.],
[ 67., 181.]])
还可以使用 @ 符号:
x @ y
array([[ 28., 64.],
[ 67., 181.]])
我们看下都有哪些运算:
乘积运算:
| 操作符 | 描述 |
|---|---|
| dot(a, b[, out]) | 矩阵点积 |
| linalg.multi_dot(arrays, *[, out]) | 多个矩阵点积 |
| vdot(a, b) | 向量点积 |
| inner(a, b) | 两个数组的内积 |
| outer(a, b[, out]) | 两个向量的外积 |
| matmul(x1, x2, /[, out, casting, order, …]) | 两个矩阵的对应位的乘积 |
| tensordot(a, b[, axes]) | 计算沿指定轴的张量点积 |
| einsum(subscripts, *operands[, out, dtype, …]) | 爱因斯坦求和约定 |
| einsum_path(subscripts, *operands[, optimize]) | 通过考虑中间数组的创建,评估einsum表达式的最低成本收缩顺序。 |
| linalg.matrix_power(a, n) | 矩阵的幂运算 |
| kron(a, b) | 矩阵的Kronecker乘积 |
分解运算:
| 操作符 | 描述 |
|---|---|
| linalg.cholesky(a) | Cholesky 分解 |
| linalg.qr(a[, mode]) | 计算矩阵的qr因式分解 |
| linalg.svd(a[, full_matrices, compute_uv, …]) | 奇异值分解 |
本征值和本征向量:
| 操作 | 描述 |
|---|---|
| linalg.eig(a) | 计算方阵的特征值和右特征向量。 |
| linalg.eigh(a[, UPLO]) | 返回复数Hermitian(共轭对称)或实对称矩阵的特征值和特征向量。 |
| linalg.eigvals(a) | 计算通用矩阵的特征值。 |
| linalg.eigvalsh(a[, UPLO]) | 计算复数Hermitian(共轭对称)或实对称矩阵的特征值。 |
基准值:
| 操作 | 描述 |
|---|---|
| linalg.norm(x[, ord, axis, keepdims]) | 矩阵或向量范数 |
| linalg.cond(x[, p]) | Compute the condition number of a matrix. |
| linalg.det(a) | 矩阵行列式 |
| linalg.matrix_rank(M[, tol, hermitian]) | 使用SVD方法返回数组的矩阵秩 |
| linalg.slogdet(a) | 计算数组行列式的符号和(自然)对数。 |
| trace(a[, offset, axis1, axis2, dtype, out]) | 返回沿数组对角线的和。 |
求解和反转:
| 操作 | 描述 |
|---|---|
| linalg.solve(a, b) | 求解线性矩阵方程或线性标量方程组。 |
| linalg.tensorsolve(a, b[, axes]) | 对x求解张量方程’a x = b’。 |
| linalg.lstsq(a, b[, rcond]) | 将最小二乘解返回线性矩阵方程 |
| linalg.inv(a) | 计算矩阵的(乘法)逆。 |
| linalg.pinv(a[, rcond, hermitian]) | 计算矩阵的(Moore-Penrose)伪逆。 |
| linalg.tensorinv(a[, ind]) | 计算N维数组的“逆”。 |
随机数
很多时候我们都需要生成随机数,在NumPy中随机数的生成非常简单:
samples = np.random.normal(size=(4, 4))
samples
array([[-2.0016, -0.3718, 1.669 , -0.4386],
[-0.5397, 0.477 , 3.2489, -1.0212],
[-0.5771, 0.1241, 0.3026, 0.5238],
[ 0.0009, 1.3438, -0.7135, -0.8312]])
上面用normal来得到一个标准正态分布的4×4样本数组。
使用np.random要比使用Python自带的随机数生成器要快得多。
np.random可以指定生成随机数的种子:
np.random.seed(1234)
numpy.random的数据生成函数使用了全局的随机种子。要避免 全局状态,你可以使用numpy.random.RandomState,创建一个 与其它隔离的随机数生成器:
rng = np.random.RandomState(1234)
rng.randn(10)
本文已收录于 http://www.flydean.com/10-python-numpy-func/
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!
最后
以上就是大意蚂蚁最近收集整理的关于NumPy之:ndarray中的函数简介简单函数矢量化数组运算条件逻辑表达式统计方法布尔数组排序文件线性代数随机数的全部内容,更多相关NumPy之:ndarray中内容请搜索靠谱客的其他文章。








发表评论 取消回复