3.2.3 多元线性回归
当输入属性有多个的时候,例如西瓜有色泽、根蒂和敲声等属性,每个西瓜的一系列属性标识为:
x
i
=
(
x
i
1
;
x
i
2
;
.
.
.
;
x
i
d
)
,
y
i
∈
R
boldsymbol{x}_i=(x_{i1};x_{i2};...;x_{id}),y_i in mathbb{R}
xi=(xi1;xi2;...;xid),yi∈R
则
w
w
w 有多个才能确定其预测标记
w
=
(
w
1
;
w
2
;
…
;
w
d
)
w=(w_1;w_2;dots;w_d)
w=(w1;w2;…;wd)
所有的西瓜数据标识为:
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
m
,
y
m
)
}
D=left{({x}_1,y_1), ({x}_2,y_2), ..., ({x}_m,y_m)right}
D={(x1,y1),(x2,y2),...,(xm,ym)}
则目标函数
y
=
w
x
+
b
y=wx+b
y=wx+b需要写成:
f
(
x
i
)
=
w
T
x
i
+
b
=
w
1
∗
x
i
1
+
w
2
∗
x
i
2
+
⋯
+
w
d
∗
x
i
d
+
b
begin{aligned} f(boldsymbol{x}_i)&=boldsymbol{w}^Tboldsymbol{x}_i + b \&= w_1*x_{i1}+w_2*x_{i2}+dots+w_d*x_{id}+b end{aligned}
f(xi)=wTxi+b=w1∗xi1+w2∗xi2+⋯+wd∗xid+b
使得
f
(
x
i
)
≃
y
i
f(boldsymbol{x}_i) simeq y_i
f(xi)≃yi
问题求解
如何确定 w boldsymbol{w} w 和 b b b ?
公式(3.4)是最小二乘法运用在一元线性回归上的情形,那么对于多元线性回归来说,我们可以类似得到
(
w
∗
,
b
∗
)
=
arg
min
(
w
,
b
)
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
=
arg
min
(
w
,
b
)
∑
i
=
1
m
(
y
i
−
f
(
x
i
)
)
2
=
arg
min
(
w
,
b
)
∑
i
=
1
m
(
y
i
−
(
w
T
x
i
+
b
)
)
2
begin{aligned} left(boldsymbol{w}^{*}, b^{*}right)&=underset{(boldsymbol{w}, b)}{arg min } sum_{i=1}^{m}left(fleft(boldsymbol{x}_{i}right)-y_{i}right)^{2} \ &=underset{(boldsymbol{w}, b)}{arg min } sum_{i=1}^{m}left(y_{i}-fleft(boldsymbol{x}_{i}right)right)^{2}\ &=underset{(boldsymbol{w}, b)}{arg min } sum_{i=1}^{m}left(y_{i}-left(boldsymbol{w}^mathrm{T}boldsymbol{x}_{i}+bright)right)^{2} end{aligned}
(w∗,b∗)=(w,b)argmini=1∑m(f(xi)−yi)2=(w,b)argmini=1∑m(yi−f(xi))2=(w,b)argmini=1∑m(yi−(wTxi+b))2
将权重与参数合为一个向量 w ^ = ( w ; b ) hat{boldsymbol{w}}=(boldsymbol{w};b) w^=(w;b),这里将b记为 w d + 1 w_d+1 wd+1,则 w ^ = ( w 1 ; w 2 ; … ; w d ; w d + 1 ) T hat{w}=(w_1;w_2;dots;w_d;w_{d+1})^T w^=(w1;w2;…;wd;wd+1)T
相应的,把数据集
D
D
D表示为一个
m
×
(
d
+
1
)
m times (d+1)
m×(d+1) 大小的矩阵
X
mathbf{X}
X
X
=
(
x
11
x
12
⋅
⋅
⋅
x
1
d
1
x
21
x
22
⋅
⋅
⋅
x
2
d
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x
m
1
x
m
2
⋅
⋅
⋅
x
m
d
1
)
=
(
x
1
T
1
x
2
T
1
.
.
.
.
.
.
x
m
T
1
)
=
(
x
^
1
T
x
^
2
T
.
.
.
x
^
m
T
)
mathbf{X} = begin{pmatrix} x_{11} & x_{12} & ··· & x_{1d} & 1 \\ x_{21} & x_{22} & ··· & x_{2d} & 1 \\ ... & ... & ... & ... & ...\\ x_{m1} & x_{m2} & ··· & x_{md} & 1 \\ end{pmatrix} = begin{pmatrix} boldsymbol{x}_1^T & 1 \\ boldsymbol{x}_2^T & 1 \\ ... & ...\\ boldsymbol{x}_m^T & 1 \\ end{pmatrix} =begin{pmatrix} hat{boldsymbol{x}}_1^T \\ hat{boldsymbol{x}}_2^T\\ ...\\ hat{boldsymbol{x}}_m^T \\end{pmatrix}
X=⎝
⎛x11x21...xm1x12x22...xm2⋅⋅⋅⋅⋅⋅...⋅⋅⋅x1dx2d...xmd11...1⎠
⎞=⎝
⎛x1Tx2T...xmT11...1⎠
⎞=⎝
⎛x^1Tx^2T...x^mT⎠
⎞
则
f
(
x
^
i
)
f(hat{boldsymbol{x}}_i)
f(x^i)可以为
f
(
x
^
i
)
=
w
1
∗
x
i
1
+
w
2
∗
x
i
2
+
⋯
+
w
d
∗
x
i
d
+
b
+
w
d
+
1
∗
1
=
w
T
x
^
i
f(hat{boldsymbol{x}}_i)=w_1*x_{i1}+w_2*x_{i2}+dots+w_d*x_{id}+b+w_{d+1}*1 \ =boldsymbol{w}^T hat{boldsymbol{x}}_i
f(x^i)=w1∗xi1+w2∗xi2+⋯+wd∗xid+b+wd+1∗1=wTx^i
则均方误差为:
E
w
^
=
∑
i
=
1
m
(
y
i
−
f
(
x
^
i
)
)
2
=
∑
i
=
1
m
(
y
i
−
w
^
T
x
^
i
)
2
=
[
y
1
−
x
^
1
T
w
^
⋯
y
m
−
x
^
m
T
w
^
]
[
y
1
−
x
^
1
T
w
^
⋮
y
m
−
x
^
m
T
w
^
]
E_{hat{boldsymbol w}}=sum_{i=1}^{m}(y_i-f(hat{boldsymbol{x}}_i))^2=sum_{i=1}^{m}(y_i-{hat{w}^That{x}_i)}^2\=begin{bmatrix} y_{1}-hat{boldsymbol{x}}_{1}^mathrm{T}hat{boldsymbol{w}} & cdots & y_{m}-hat{boldsymbol{x}}_{m}^mathrm{T}hat{boldsymbol{w}} \ end{bmatrix} begin{bmatrix} y_{1}-hat{boldsymbol{x}}_{1}^mathrm{T}hat{boldsymbol{w}} \ vdots \ y_{m}-hat{boldsymbol{x}}_{m}^mathrm{T}hat{boldsymbol{w}} end{bmatrix}
Ew^=i=1∑m(yi−f(x^i))2=i=1∑m(yi−w^Tx^i)2=[y1−x^1Tw^⋯ym−x^mTw^]⎣
⎡y1−x^1Tw^⋮ym−x^mTw^⎦
⎤
其中
[
y
1
−
x
^
1
T
w
^
⋮
y
m
−
x
^
m
T
w
^
]
=
[
y
1
⋮
y
m
]
−
[
x
^
1
T
w
^
⋮
x
^
m
T
w
^
]
=
y
−
[
x
^
1
T
⋮
x
^
m
T
]
⋅
w
^
=
y
−
X
w
^
begin{aligned} begin{bmatrix} y_{1}-hat{boldsymbol{x}}_{1}^mathrm{T}hat{boldsymbol{w}} \ vdots \ y_{m}-hat{boldsymbol{x}}_{m}^mathrm{T}hat{boldsymbol{w}} end{bmatrix}&=begin{bmatrix} y_{1} \ vdots \ y_{m} end{bmatrix}-begin{bmatrix} hat{boldsymbol{x}}_{1}^mathrm{T}hat{boldsymbol{w}} \ vdots \ hat{boldsymbol{x}}_{m}^mathrm{T}hat{boldsymbol{w}} end{bmatrix}\ &=boldsymbol{y}-begin{bmatrix} hat{boldsymbol{x}}_{1}^mathrm{T} \ vdots \ hat{boldsymbol{x}}_{m}^mathrm{T} end{bmatrix}cdothat{boldsymbol{w}}\ &=boldsymbol{y}-mathbf{X}hat{boldsymbol{w}} end{aligned}
⎣
⎡y1−x^1Tw^⋮ym−x^mTw^⎦
⎤=⎣
⎡y1⋮ym⎦
⎤−⎣
⎡x^1Tw^⋮x^mTw^⎦
⎤=y−⎣
⎡x^1T⋮x^mT⎦
⎤⋅w^=y−Xw^
注意这个
w
^
hat{w}
w^并不是一个数,而是一个m行的列向量
所以:
E
w
^
=
(
y
−
X
w
^
)
T
(
y
−
X
w
^
)
(3.9)
E_{hat{boldsymbol w}}={(boldsymbol{y}-mathbf{X}hat{boldsymbol{w}})}^T(boldsymbol{y}-mathbf{X}hat{boldsymbol{w}}) tag{3.9}
Ew^=(y−Xw^)T(y−Xw^)(3.9)
求
w
^
hat{w}
w^的最优解,先要补充一下知识
凸集:
定义:设集合 D ∈ R n D in R^{n} D∈Rn, 如果对任意的 x boldsymbol{x} x, y ∈ D boldsymbol{y} in D y∈D与任意的 a ∈ [ 0 , 1 ] a in[0,1] a∈[0,1],有 a x + ( 1 − a ) y ∈ D a boldsymbol{x}+(1-a) boldsymbol{y} in D ax+(1−a)y∈D, 则称集合 D 是凸集。
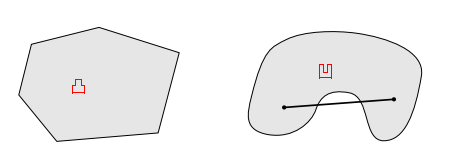
梯度:
梯度定义:设 n mathrm{n} n元函数 f ( x ) f(boldsymbol{x}) f(x)对自变量 x = ( x 1 , x 2 , … , x n ) T boldsymbol{x}=left(x_{1}, x_{2}, ldots, x_{n}right)^{T} x=(x1,x2,…,xn)T的各分量 x i x_{i} xi的偏导数 ∂ f ( x ) ∂ x i ( i = 1 , 2 , … , n ) frac{partial f(boldsymbol{x})}{partial x_{i}}(i=1,2, ldots, n) ∂xi∂f(x)(i=1,2,…,n)都存在,则称函数 f ( x ) f(boldsymbol{x}) f(x)在 x boldsymbol{x} x处一阶可导, 并称向量
∇
f
(
x
)
=
(
∂
f
(
x
)
∂
x
1
∂
f
(
x
)
∂
x
2
⋮
∂
f
(
x
)
∂
x
n
)
nabla f(boldsymbol{x})=left(begin{array}{c} frac{partial f(boldsymbol{x})}{partial x_{1}} \ frac{partial f(boldsymbol{x})}{partial x_{2}} \ vdots \ frac{partial f(boldsymbol{x})}{partial x_{n}} end{array}right)
∇f(x)=⎝
⎛∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)⎠
⎞
为函数
f
(
x
)
f(boldsymbol{x})
f(x) 在
x
boldsymbol{x}
x处的一阶导数或梯度, 记为
∇
f
(
x
)
nabla f(boldsymbol{x})
∇f(x)(列向量)
Hessian矩阵
Hessian (海塞) 矩阵定义:设 n mathrm{n} n元函数 f ( x ) f(boldsymbol{x}) f(x)对自变量 x = ( x 1 , x 2 , … , x n ) T boldsymbol{x}=left(x_{1}, x_{2}, ldots, x_{n}right)^{T} x=(x1,x2,…,xn)T的各 分量 x i x_{i} xi的二阶偏导数 ∂ 2 f ( x ) ∂ x i ∂ x j ( i = 1 , 2 , … , n ; j = 1 , 2 , … , n ) frac{partial^{2} f(boldsymbol{x})}{partial x_{i} partial x_{j}} quad(i=1,2, ldots, n ; j=1,2, ldots, n) ∂xi∂xj∂2f(x)(i=1,2,…,n;j=1,2,…,n)都存在,则称函数 f ( x ) f(boldsymbol{x}) f(x)在 点 x boldsymbol{x} x处二阶可导, 并称矩阵为 f ( x ) f(boldsymbol{x}) f(x)在 x boldsymbol{x} x处的二阶导数或Hessian矩阵,记为 ∇ 2 f ( x ) nabla^{2} f(boldsymbol{x}) ∇2f(x),若 f ( x ) f(boldsymbol{x}) f(x)对 x boldsymbol{x} x各变元 的所有二阶偏导数都连续, 则 ∂ 2 f ( x ) ∂ x i ∂ x j = ∂ 2 f ( x ) ∂ x j ∂ x i frac{partial^{2} f(boldsymbol{x})}{partial x_{i} partial x_{j}}=frac{partial^{2} f(boldsymbol{x})}{partial x_{j} partial x_{i}} ∂xi∂xj∂2f(x)=∂xj∂xi∂2f(x)此时 ∇ 2 f ( x ) nabla^{2} f(boldsymbol{x}) ∇2f(x)为对称矩阵。
∇ 2 f ( x ) = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x 1 ∂ x n ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 ⋯ ∂ 2 f ( x ) ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x n 2 ] nabla^{2} f(boldsymbol{x})=left[begin{array}{cccc}frac{partial^{2} f(boldsymbol{x})}{partial x_{1}^{2}} & frac{partial^{2} f(boldsymbol{x})}{partial x_{1} partial x_{2}} & cdots & frac{partial^{2} f(boldsymbol{x})}{partial x_{1} partial x_{n}} \ frac{partial^{2} f(boldsymbol{x})}{partial x_{2} partial x_{1}} & frac{partial^{2} f(boldsymbol{x})}{partial x_{2}^{2}} & cdots & frac{partial^{2} f(boldsymbol{x})}{partial x_{2} partial x_{n}} \ vdots & vdots & ddots & vdots \ frac{partial^{2} f(boldsymbol{x})}{partial x_{n} partial x_{1}} & frac{partial^{2} f(boldsymbol{x})}{partial x_{n} partial x_{2}} & cdots & frac{partial^{2} f(boldsymbol{x})}{partial x_{n}^{2}}end{array}right] ∇2f(x)=⎣ ⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋱⋯∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)⎦ ⎤
正定矩阵:给出一个n×n的矩阵A,如果对于任意长度为n的非零向量,都有$x^TAx>$0成立,则A是正定矩阵。等价于A的所有特征值都是正的。等价于A的顺序主子式都是正的。
也许你发现了这样一个事实,
f
=
(
x
1
+
x
2
)
2
+
3
(
x
2
+
x
3
)
2
+
x
3
2
=
y
1
2
+
3
y
2
2
+
y
3
2
≥
0
f=left( x_{1}+x_{2} right)^2+3left( x_{2}+x_{3} right)^2+x_{3} ^2=y_{1}^2+3y_{2}^2+y_{3}^2geq0
f=(x1+x2)2+3(x2+x3)2+x32=y12+3y22+y32≥0
当 y 1 , y 2 , y 3 y_{1},y_{2},y_{3} y1,y2,y3不全为 0 时,这个二次型严格大于 0.
当 X 不是零向量的时候,就会有: f = X ′ A X > 0 f=X'A X>0 f=X′A X>0
我们将这样的二次型称为正定的,对称矩阵A 称为正定矩阵.
特别地,欧氏度量的平方就是最简单的正定二次型,其正定矩阵正是单位阵. 正如我们例子中的配方运算,将一般的正定二次型化为只含有平方项的二次型(对应对角矩阵)
- 一元正定二次型对应的图像正是开口朝上、顶点在原点的抛物线.
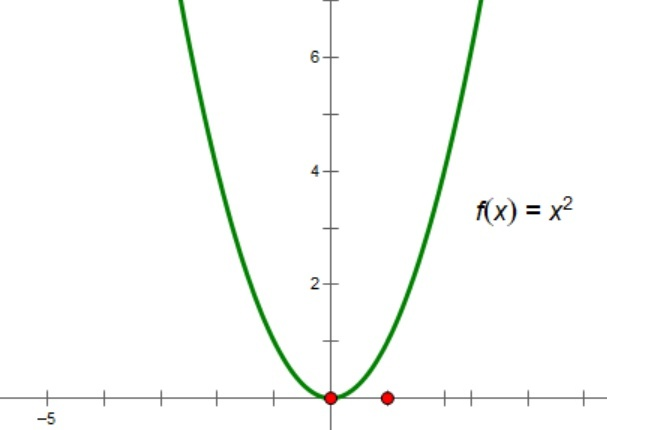
- 二元正定二次型对应的图像正是开口朝上、顶点在原点的抛物面.
于是,n 元正定二次型实际上就是 n 维空间内的抛物面.
给出一个n×n的矩阵A,如果对于任意长度为n的非零向量,都有$x^TAx>$0成立,则A是正定矩阵。等价于A的所有特征值都是正的。等价于A的顺序主子式都是正的。
多元实值函数凹凸性判定定理
设 D ⊂ R n D subset R^{n} D⊂Rn是非空开凸集, f : D ⊂ R n → R f: D subset R^{n} rightarrow R f:D⊂Rn→R,且 f ( x ) f(boldsymbol{x}) f(x)在 D 上二阶连续可 微,如果 f ( x ) f(boldsymbol{x}) f(x)的Hessian矩阵 ∇ f 2 nabla f^{2} ∇f2 在D上是正定的,则 f ( x ) f(boldsymbol{x}) f(x)是 D 上的严格凸函数。
凸充分性定理
若 f : R n → R f: R^{n} rightarrow R f:Rn→R是凸函数,且 f ( x ) f(boldsymbol{x}) f(x)一阶连续可微,则 x ∗ boldsymbol{x}^{*} x∗是全局解的充分必要 条件是 ∇ f ( x ∗ ) = 0 nabla fleft(boldsymbol{x}^{*}right)=mathbf{0} ∇f(x∗)=0,其中 ∇ f ( x ) nabla f(boldsymbol{x}) ∇f(x)为 f ( x ) f(boldsymbol{x}) f(x)关于 x boldsymbol{x} x的一阶导数(也称梯度)。
矩阵的微分公式
向量的微分公式
∂
y
∂
x
=
(
∂
y
∂
x
1
∂
y
∂
x
2
⋮
∂
y
∂
x
n
)
∂
y
∂
x
=
(
∂
y
∂
x
1
∂
y
∂
x
2
⋯
∂
y
∂
x
n
)
frac{partial y}{partial x}=left(begin{array}{c} frac{partial y}{partial x_{1}} \ frac{partial y}{partial x_{2}} \ vdots \ frac{partial y}{partial x_{n}} end{array}right) \ quad frac{partial y}{partial x}=left(begin{array}{cccc} frac{partial y}{partial x_{1}} & frac{partial y}{partial x_{2}} & cdots & frac{partial y}{partial x_{n}} end{array}right)
∂x∂y=⎝
⎛∂x1∂y∂x2∂y⋮∂xn∂y⎠
⎞∂x∂y=(∂x1∂y∂x2∂y⋯∂xn∂y)
默认采用分母布局,即第一种(第二种为分子布局)
其中, x = ( x 1 , x 2 , … , x n ) T boldsymbol{x}=left(x_{1}, x_{2}, ldots, x_{n}right)^{T} x=(x1,x2,…,xn)T 为 n mathrm{n} n维列向量, y mathcal{y} y 为 C boldsymbol{C} C 的 n mathrm{n} n 元标量函数
由标量-向量的矩阵微分公式可推得:
∂
x
T
a
∂
x
=
∂
a
T
x
∂
x
=
(
∂
(
a
1
x
1
+
a
2
x
2
+
…
+
a
n
x
n
)
∂
x
1
∂
(
a
1
x
1
+
a
2
x
2
+
…
+
a
n
x
n
)
∂
x
2
⋮
∂
(
a
1
x
1
+
a
2
x
2
+
…
+
a
n
x
n
)
∂
x
n
)
=
(
a
1
a
2
⋮
a
n
)
=
a
frac{partial boldsymbol{x}^{T} boldsymbol{a}}{partial boldsymbol{x}}=frac{partial boldsymbol{a}^{T} boldsymbol{x}}{partial boldsymbol{x}}=left(begin{array}{c} frac{partialleft(a_{1} x_{1}+a_{2} x_{2}+ldots+a_{n} x_{n}right)}{partial x_{1}} \ frac{partialleft(a_{1} x_{1}+a_{2} x_{2}+ldots+a_{n} x_{n}right)}{partial x_{2}} \ vdots \ frac{partialleft(a_{1} x_{1}+a_{2} x_{2}+ldots+a_{n} x_{n}right)}{partial x_{n}} end{array}right)=left(begin{array}{c} a_{1} \ a_{2} \ vdots \ a_{n} end{array}right)=boldsymbol{a}
∂x∂xTa=∂x∂aTx=⎝
⎛∂x1∂(a1x1+a2x2+…+anxn)∂x2∂(a1x1+a2x2+…+anxn)⋮∂xn∂(a1x1+a2x2+…+anxn)⎠
⎞=⎝
⎛a1a2⋮an⎠
⎞=a
正定矩阵微分公式:
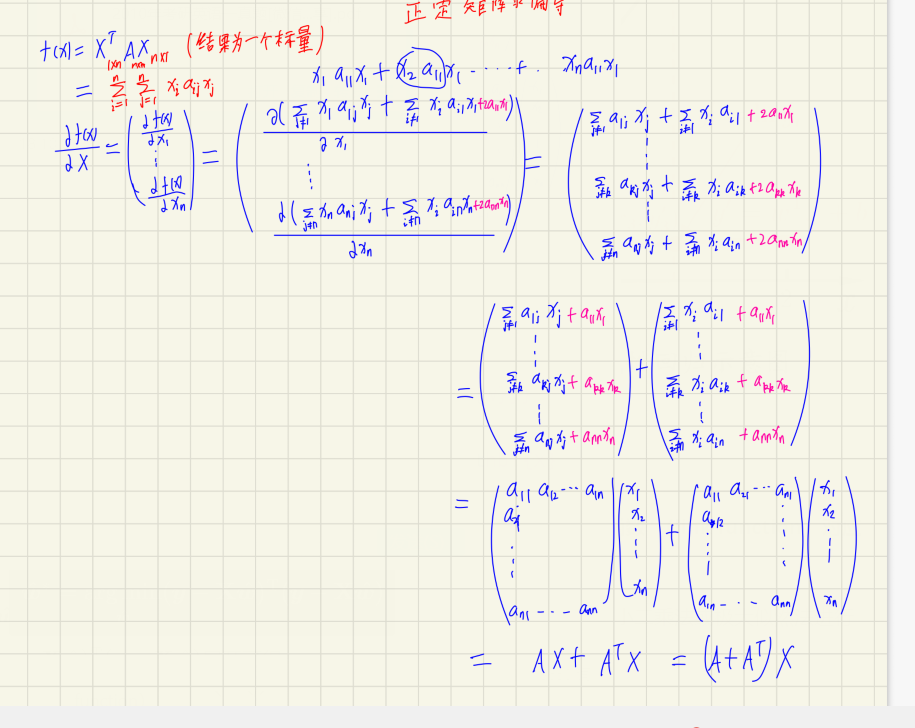
行向量 y T y^{T} yT 对列向量 x x x 求导
注意
1
×
n
1 times n
1×n 向量对
m
×
1
m times 1
m×1 向量求导后是
m
×
n
m times n
m×n 矩阵。 将
y
y
y 的每一列对
x
x
x 求偏导, 将各列构成一个矩阵。
d
y
T
d
x
=
[
∂
y
1
∂
x
1
∂
y
2
∂
x
1
⋯
∂
y
n
∂
x
1
∂
y
1
∂
x
2
∂
y
2
∂
x
2
⋯
∂
y
n
∂
x
2
⋮
⋮
⋱
⋮
∂
y
1
∂
x
m
∂
y
2
∂
x
m
⋯
∂
y
n
∂
x
m
]
frac{mathbf{d y}^{mathrm{T}}}{mathrm{dx}}=left[begin{array}{cccc} frac{partial y_1}{partial mathrm{x}_{1}} & frac{partial y_2}{partial mathrm{x}_{1}} & cdots & frac{partial y_n}{partial mathrm{x}_{1}} \ frac{partial y_1}{partial mathrm{x}_{2}} & frac{partial y_2}{partial mathrm{x}_{2}} & cdots & frac{partial y_n}{partial mathrm{x}_{2}} \ vdots & vdots & ddots & vdots \ frac{partial y_1}{partial mathrm{x}_{mathrm{m}}} & frac{partial y_2}{partial mathrm{x}_{mathrm{m}}} & cdots & frac{partial y_n}{partial mathrm{x}_{mathrm{m}}} end{array}right]
dxdyT=⎣
⎡∂x1∂y1∂x2∂y1⋮∂xm∂y1∂x1∂y2∂x2∂y2⋮∂xm∂y2⋯⋯⋱⋯∂x1∂yn∂x2∂yn⋮∂xm∂yn⎦
⎤
d x T d x = I d ( A x ) T d x = A T begin{array}{l} frac{d mathbf{x}^{T}}{d mathbf{x}}=mathbf{I} \ frac{d(mathbf{A x})^{mathrm{T}}}{mathrm{dx}}=mathbf{A}^{mathrm{T}} end{array} dxdxT=Idxd(Ax)T=AT
有了上述理论支撑,我们总结下求损失函数最优解的步骤:
- 证明损失函数是凸函数
- 求损失函数关于 w ^ hat{w} w^的一阶导数(梯度)
- 令一阶导数等于0,解出 w ^ ∗ hat{w}^* w^∗
证明损失函数是凸函数
∂
E
w
^
∂
w
^
=
∂
∂
w
^
[
(
y
−
X
w
^
)
T
(
y
−
X
w
^
)
]
=
∂
∂
w
^
[
(
y
T
−
w
^
T
X
T
)
(
y
−
X
w
^
)
]
=
∂
∂
w
^
[
y
T
y
−
y
T
X
w
^
−
w
^
T
X
T
y
+
w
^
T
X
T
X
w
^
]
=
∂
y
T
y
∂
w
^
−
∂
y
T
X
w
^
∂
w
^
−
∂
w
^
T
X
T
y
∂
w
^
+
∂
w
^
T
X
T
X
w
^
∂
w
^
begin{aligned} frac{partial E_{hat{boldsymbol{w}}}}{partial hat{boldsymbol{w}}} &=frac{partial}{partial hat{boldsymbol{w}}}left[(boldsymbol{y}-mathbf{X} hat{boldsymbol{w}})^{T}(boldsymbol{y}-mathbf{X} hat{boldsymbol{w}})right] \ &=frac{partial}{partial hat{boldsymbol{w}}}left[left(boldsymbol{y}^{T}-hat{boldsymbol{w}}^{T} mathbf{X}^{T}right)(boldsymbol{y}-mathbf{X} hat{boldsymbol{w}})right] \ &=frac{partial}{partial hat{boldsymbol{w}}}left[{boldsymbol{y}}^{T} boldsymbol{y}-boldsymbol{y}^{T} mathbf{X} hat{boldsymbol{w}}-hat{boldsymbol{w}}^{T} mathbf{X}^{T} boldsymbol{y}+hat{boldsymbol{w}}^{T} mathbf{X}^{T} mathbf{X} hat{boldsymbol{w}}right] \ &= cfrac{partial boldsymbol{y}^{mathrm{T}}boldsymbol{y}}{partial hat{boldsymbol w}}-cfrac{partial boldsymbol{y}^{mathrm{T}}mathbf{X}hat{boldsymbol w}}{partial hat{boldsymbol w}}-cfrac{partial hat{boldsymbol w}^{mathrm{T}}mathbf{X}^{mathrm{T}}boldsymbol{y}}{partial hat{boldsymbol w}}+cfrac{partial hat{boldsymbol w}^{mathrm{T}}mathbf{X}^{mathrm{T}}mathbf{X}hat{boldsymbol w}}{partial hat{boldsymbol w}} end{aligned}
∂w^∂Ew^=∂w^∂[(y−Xw^)T(y−Xw^)]=∂w^∂[(yT−w^TXT)(y−Xw^)]=∂w^∂[yTy−yTXw^−w^TXTy+w^TXTXw^]=∂w^∂yTy−∂w^∂yTXw^−∂w^∂w^TXTy+∂w^∂w^TXTXw^
由矩阵微分公式
∂ a T x ∂ x = ∂ x T a ∂ x = a , ∂ x T A x ∂ x = ( A + A T ) x cfrac{partialboldsymbol{a}^{mathrm{T}}boldsymbol{x}}{partialboldsymbol{x}}=cfrac{partialboldsymbol{x}^{mathrm{T}}boldsymbol{a}}{partialboldsymbol{x}}=boldsymbol{a},cfrac{partialboldsymbol{x}^{mathrm{T}}mathbf{A}boldsymbol{x}}{partialboldsymbol{x}}=(mathbf{A}+mathbf{A}^{mathrm{T}})boldsymbol{x} ∂x∂aTx=∂x∂xTa=a,∂x∂xTAx=(A+AT)x
( X T X ) T = X T ( X T ) T = X T X (X^TX)^T=X^T(X^T)^T=X^TX (XTX)T=XT(XT)T=XTX
得:
∂
E
w
^
∂
w
^
=
0
−
X
T
y
−
X
T
y
+
(
X
T
X
+
X
T
X
)
w
^
=
2
X
T
(
X
w
^
−
y
)
(3.10)
cfrac{partial E_{hat{boldsymbol w}}}{partial hat{boldsymbol w}} = 0-mathbf{X}^{mathrm{T}}boldsymbol{y}-mathbf{X}^{mathrm{T}}boldsymbol{y}+(mathbf{X}^{mathrm{T}}mathbf{X}+mathbf{X}^{mathrm{T}}mathbf{X})hat{boldsymbol w} \ =2mathbf{X}^{mathrm{T}}(mathbf{X}hat{boldsymbol w}-boldsymbol{y}) tag{3.10}
∂w^∂Ew^=0−XTy−XTy+(XTX+XTX)w^=2XT(Xw^−y)(3.10)
再求二阶偏导数
∂
2
E
w
^
∂
w
^
2
=
∂
∂
w
^
(
∂
E
w
^
∂
w
^
)
=
∂
∂
w
^
(
2
X
T
X
w
^
−
2
X
T
y
)
)
=
2
X
T
X
begin{align*} cfrac{{partial}^2 E_{hat{boldsymbol w}}}{partial hat{boldsymbol w}^2}&=cfrac{partial}{partialhat{w}}(cfrac{partial E_{hat{boldsymbol w}}}{partial hat{boldsymbol w}})\ &= cfrac{partial}{partialhat{w}}(2mathbf{X}^{mathrm{T}}mathbf{X}hat{boldsymbol w}-2X^Tboldsymbol{y}) ) \&=2mathbf{X}^{mathrm{T}}mathbf{X} end{align*}
∂w^2∂2Ew^=∂w^∂(∂w^∂Ew^)=∂w^∂(2XTXw^−2XTy))=2XTX
上式即为Hessian矩阵,当然Hessian矩阵并不一定是正定矩阵,因为我们输入的数据不同,不经过处理是不能判断正定的,但西瓜书上直接假设了是正定的,然后可以利用凸充分性定理来解出
w
^
hat{w}
w^
以上证明了
E
w
^
E_{hat{boldsymbol w}}
Ew^为凸函数,下面让一阶导数等于0,即
∂
E
w
^
∂
w
^
=
2
X
T
X
w
^
−
2
X
T
y
=
0
cfrac{partial E_{hat{boldsymbol w}}}{partial hat{boldsymbol w}}=2mathbf{X}^{mathrm{T}}mathbf{X}hat{boldsymbol w}-2X^Tboldsymbol{y}=0
∂w^∂Ew^=2XTXw^−2XTy=0
X T X w ^ = X T y mathbf{X}^{mathrm{T}}mathbf{X}hat{boldsymbol w}=X^Tboldsymbol{y} XTXw^=XTy
两边同乘
(
X
T
X
)
−
1
(mathbf{X}^{mathrm{T}}mathbf{X})^{-1}
(XTX)−1,得
w
^
=
(
X
T
X
)
−
1
X
T
y
(3.11)
hat{boldsymbol w}=(mathbf{X}^{mathrm{T}}mathbf{X})^{-1}X^Tboldsymbol{y} tag{3.11}
w^=(XTX)−1XTy(3.11)
- 令
x
^
i
=
(
x
i
;
1
)
hat{boldsymbol{x}}_i=(boldsymbol{x}_i;1)
x^i=(xi;1),则最终学得的多元线性回归模型为
f ( x ^ i ) = w T x ^ i = x ^ i T ( X T X ) − 1 X T y f(hat{boldsymbol{x}}_i) =boldsymbol{w}^T hat{boldsymbol{x}}_i\ = hat{boldsymbol{x}}_i^{mathbf{T}}(mathbf{X^TX})^{-1}mathbf{X}^{mathbf{T}}boldsymbol{y} f(x^i)=wTx^i=x^iT(XTX)−1XTy
X mathbf{X} X不为满秩矩阵或不是正定矩阵时,可解出多个 w ^ hat{boldsymbol{w}} w^,它们都能使均方误差最小化
选择哪一个解是依据学习算法的归纳偏好决定(1.4节)的,最常见的做法就是引入正则化(4.4、11.4节)
-
主要教材为西瓜书,结合南瓜书,统计学习方法,B站视频整理~
-
人群定位:学过高数会求偏导、线代会矩阵运算、概率论知道啥是随机变量
-
原理讲解,公式推导,课后习题,实践代码应有尽有,欢迎订阅
-
代码实践部分将发布于公众号 小白白学技术
-
获取多资料 关注公众号 小白白学技术
最后
以上就是温柔早晨最近收集整理的关于西瓜书研读——第三章 线性模型:多元线性回归的全部内容,更多相关西瓜书研读——第三章内容请搜索靠谱客的其他文章。








发表评论 取消回复