leetcode — 46. 全排列（不含重复数字）

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

        回溯法：一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解被确认不是一个解（或者至少不是最后一个解），回溯算法会通过在上一步进行一些变化抛弃该解，即回溯并且再次尝试。

方法：回溯

        问题等价：有 n 个排列成一行的空格，需要从左往右依此填入给定的 n 个数，每个数只能使用一次。——> 穷举法，从左往右每一个位置都依此尝试填入一个数，看能不能填完这 n 个空格，可以用「回溯法」来模拟这个过程。

定义递归函数 backtrack(first, output) 表示从左往右填到第 first 个位置，当前排列为 output。 那么整个递归函数分为两个情况：

• 如果 first==n，说明我们已经填完了 n 个位置（注意下标从 0 开始），找到了一个可行的解，将 output 放入答案数组中，递归结束。
• 如果 first<n，要考虑这第 first 个位置要填哪个数。根据题目要求不能填已经填过的数，因此很容易想到的一个处理手段是定义一个标记数组 visited[] 来标记已经填过的数，那么在填第 first 个数的时候遍历题目给定的 n 个数，如果这个数没有被标记过，就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 backtrack(first + 1, output)。回溯的时候要撤销这一个位置填的数以及标记，并继续尝试其他没被标记过的数。

        使用标记数组来处理填过的数是一个很直观的思路，但是可不可以去掉这个标记数组来降低空间复杂度呢？

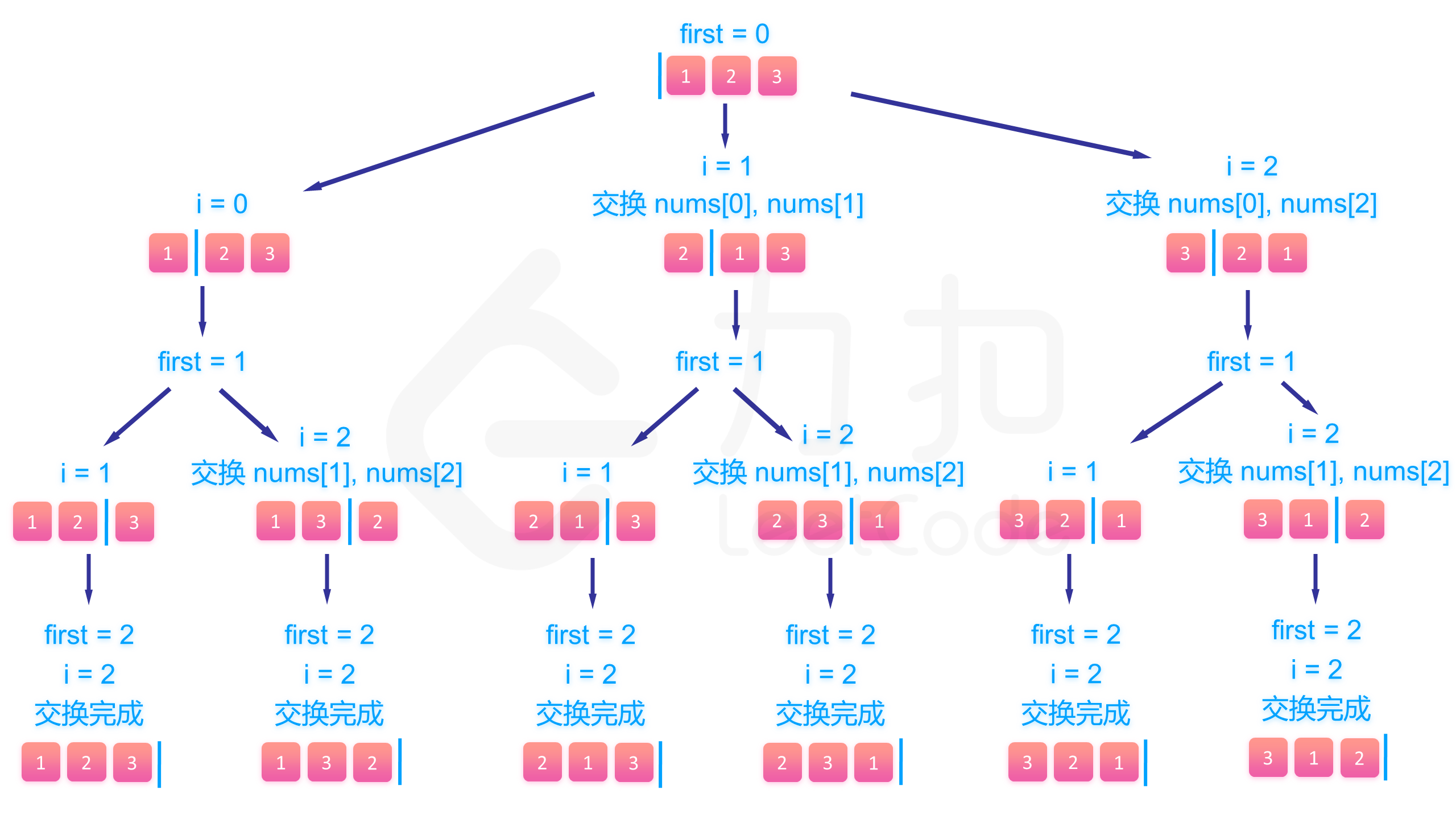
        思路：将题目给定的 n 个数的数组 nums 划分成左右两个部分，左边的表示已经填过的数，右边表示待填的数，在回溯的时候只要动态维护这个数组即可。

• 假设已经填到第 first 个位置，那么nums 数组中 [0,first−1] 是已填过的数的集合，[first,n−1] 是待填的数的集合。
• 尝试用[first,n−1] 里的数去填第 first 个数，假设待填的数的下标为 i ，那么填完以后将第 i 个数和第 first 个数交换，即能使得在填第 first+1个数的时候 nums 数组的 [0,first] 部分为已填过的数，[first+1,n−1] 为待填的数，回溯的时候交换回来即能完成撤销操作。

        举例：假设有 [2, 5, 8, 9, 10] 这 5 个数要填入，已经填到第 3 个位置，已经填了 [8,9] 两个数，那么这个数组目前为 [8, 9 | 2, 5, 10] 这样的状态，分隔符区分了左右两个部分。假设这个位置要填 10 这个数，为了维护数组，将 2 和 10 交换，即能使得数组继续保持分隔符左边的数已经填过，右边的待填 [8, 9, 10 | 2, 5] 。

        这样生成的全排列并不是按字典序存储在答案数组中的，如果题目要求按字典序输出，则用标记数组或者其他方法。

下面的图展示了回溯的整个过程：

方法一：交换进行每个位置数字的选择，不能保证字典序

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> perm = new ArrayList<>();

        for(int num : nums){
            perm.add(num);
        }

        int len = nums.length;
        backtrace(len, perm, res, 0);

        return res;
    }

    public void backtrace(int len, List<Integer> perm, List<List<Integer>> res, int first){
        // 判断结束条件
        if(first == len){
            res.add(new ArrayList<Integer>(perm));
            return;
        }

        for(int i = first; i < len; i ++){
            // 动态维护数组
            Collections.swap(perm, first, i);
            // 递归进行下一个数的选择
            backtrace(len, perm, res, first + 1);
            // 撤销操作
            Collections.swap(perm, first, i);
        }
    }
}

方法二：先排序使得按照字典序输出

class Solution {
	public static List<List<Integer>> permute(int[] nums) {

		// 回溯法+递归
		// 声明返回值的存储空间
		List<List<Integer>> lists = new ArrayList<>();
		
		// 判断数组中元素的个数
		if(nums.length == 0) {
			return lists;
		}
		
		// 声明空间
		ArrayList<Integer> al = new ArrayList<>();
		// 排序
		Arrays.sort(nums);
		// 回溯遍历
		depthFirstSearch(lists, al, nums);

		return lists;
	}

	public static void depthFirstSearch(List<List<Integer>> lists, ArrayList<Integer> al, int[] nums) {

		// 判断数组元素，到达叶子节点，将路径装入结果列表
		if (nums.length == al.size()) {
			lists.add(new ArrayList<>(al));
			return;
		} else {
			for (int i = 0; i < nums.length; i++) {
                // 排除不合法的选择，不能重复
				if(al.contains(nums[i])) {
					continue;
				}
                // 做选择
				al.add(nums[i]);
				// 递归调用，进入下一层
				depthFirstSearch(lists, al, nums);
				// 状态重置，撤销当前选择
				al.remove(al.size() - 1);
			}
		}
	}
}

方法三：访问数组标记

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> perm = new ArrayList<>();

        if(nums.length == 0){
            return res;
        }
        boolean[] used = new boolean[nums.length];
        backtrace(perm, res, used, nums, 0);

        return res;
    }

    public void backtrace(List<Integer> perm, List<List<Integer>> res, boolean[] used, int[] nums, int depth){
        // 判断结束条件
        if(depth == nums.length){
            res.add(new ArrayList<Integer>(perm));
            return;
        }
        // 对每个元素进行判断，如果没有使用则进入回溯
        for (int i = 0; i < used.length; i++) {
            if (!used[i]) {
                perm.add(nums[i]);
                used[i] = true;
                backtrace(perm, res, used, nums, depth + 1);
                perm.remove(perm.size() - 1);
                used[i] = false;
            }
        }

    }

}

「为什么在往结果集中添加排列结果的时候，需要进行new ArrayList添加」

        假设这段代码，「正确」res.add(new ArrayList<>(output)); 变为「错误」res.add(output); 关键在于res存放的是list引用。 那么回溯过程中，将数字使用状态重置撤销的时候，会将list的元素移除掉，也会影响到res里面的list情况。因为它们是同一个引用。 全部为空，是因为回溯结束的同时，会将全部数字重置撤销，这样list里面的元素就会为空了，同样的，也会影响到res的存放情况。

最后

以上就是英俊丝袜为你收集整理的leetcode — 46. 全排列（不含重复数字）的全部内容，希望文章能够帮你解决leetcode — 46. 全排列（不含重复数字）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。