第8章 矩阵和线性变换

● 包含平移的变换称作仿射变换， 3D 中 的仿射变换不能用 3*3 矩阵表达， 而是用4*4 矩阵来表达。

● 在旋转坐标系时， 物体上的点实际没有移动， 我们只是在另外一个坐标系中描述它的位置而已。

● 只需记住可以变换物体， 也可以变换坐标系， 这两种变换实际上是等价的， 将物体变换一个量 等价于 坐标系变换一个相反的量。

● 一般来说， 变换物体相当于以相反的量变换描述这个物体的坐标系

● 注意 ： 当有多个变换时， 则需要以相反的顺序变换相反的量。 例如 ： 将物体顺时针针旋转 20°， 扩大200%， 等价于将坐标系缩小200%， 再逆时针旋转20°

* 2D 旋 转*

● 在 2D 环境中，物体只能绕某个点旋转， 在2D 中绕原点旋转只有一个参数： 角度θ， 它描述了旋转量。 逆时针旋转经常（不是必须）被认为是正方向，顺时针方向是负方向。

3D 中绕坐标轴的选择

● 在 3D 场景中， 绕轴旋转而不是点（此时， 轴指的是旋转所绕的直线， 不一定是 笛卡尔坐标轴 x, y 或 z）, 这里只讨论旋转轴穿过原点的情况，

● 绕轴旋转 θ°时， 必须知道哪个方向被认为 “正”， 哪个方向被认为 “负”， 左手坐标系定义此方向为左手法则。

● 最为常见的选择是绕某坐标轴的简单旋转， 比如绕 x 轴旋转。

缩放

● 如果在各方向上应用同比例的缩放， 并且沿原点“膨胀”物体， 那么就是均匀缩放。 均匀缩放可以保持物体的角度和比例不变，如果长度增加或减小因子k， 则面积增加或减小因子 k², 在3D中，体积的因子是 k³。

● 如果需要“挤压”或“拉伸”物体， 在不同的方向应用不同的因子即可， 这称作非均匀缩放。非均匀缩放时， 物体角度将发生变化。 视各方向缩放因子的不同， 长度、面积、体积的变化因子也各不相同

● 如果 | k | < 1， 物体将 “变短“， 如果 | k| >1, 物体将 “变长”。 如果 k=0， 就是正交投影。 如果 k<0 就是镜像， 应用非均匀缩放的效果类似于切变。 事实上，非均匀缩放和切变是很难区分的。

沿坐标轴的缩放

● 最简单的缩放方法是沿着每个坐标轴应用单独的缩放因子。 缩放时沿着垂直的轴（2D中）或平面（3D中）进行的。 如果每个轴的缩放因子相同，就是均匀缩放， 否则就是非均匀缩放。

● 在2D 中有两个缩放因子， kx 和ky。

● 3D 缩放矩阵公式如：

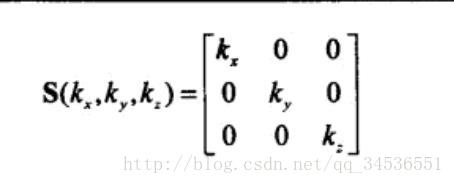
沿任意方向缩放

● 通过基向量构造矩阵，得到以单位向量n 为缩放方向， k 为因子的缩放矩阵：

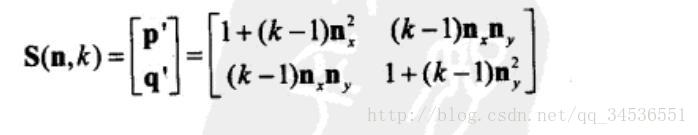
● 以单位向量n 为缩放方向， k 为因子的3D 缩放矩阵如公式：

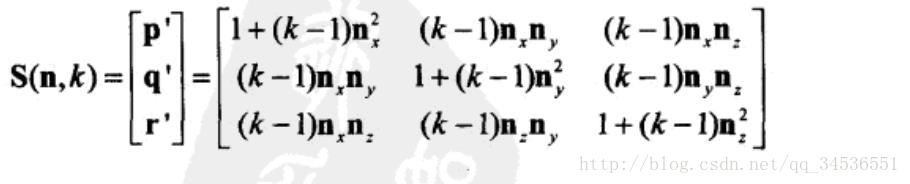
正交投影

● 一般来说， 投影意味着降维操作， 有一种投影方法是某个方向上用0 作为缩放因子， 在这种情况下， 所有点都被拉平至垂直的轴 （2D）或平面 （3D）上， 这种类型的投影称作 正交投影或者平行投影

● 最简单的投影方式是向坐标轴 （2D）或平面（3D）投影。 向坐标轴或平面投影在实际变换中不常发生， 大多数情况是向低维的变量赋值， 且要抛弃维数时，例如， 将3D 点赋值给 2D 点， 抛弃 z 分量， 只复制 x 和 y.

镜 像

● 镜像（也叫作反射）是一种变换， 其作用是将物体沿直线（2D中）或平面（3D中）“泛着”，

● 使缩放因子为-1就能够很容易地实现镜像变换， 注意 ： 一个物体只能“镜像”一次， 如果再次镜像（当沿不同的轴或平面的时候）， 物体将翻回“正面”。

切 变

● 切变是一种坐标系“扭曲”变换， 非均匀地拉伸它。 切变的时候角度会发生变化， 但令人惊奇的是面积和体积去保持不变。 基本思想是将某一坐标的乘积加到另一个上。

● 切变是一种很少用到的变换，它也被称作 扭曲变换。 包含切变与缩放（均匀或非均匀）的变换通常很容易与包含旋转与非均匀缩放（只能是非均匀）的变换发生混淆。

仿射变换

● 仿射变换是指线性变换后接着平移，仿射变换的集合是线性变换的超集， 任何线性变换都是仿射变换， 但不是所有仿射变换都是线性变换。

可逆变换

● 如果存在一个逆变换可以“撤销”原变换， 那么该变换是可逆的， 一个仿射变换就是线性变换加上平移， 显然，可以用相反的量“撤销”平移部分。 所以问题变为一个线性变换是否可逆。

● 因为任意线性变换都能表达为矩阵， 所以求逆变换等价于求矩阵的逆。

●如果矩阵是奇异的， 则变换不可逆； 可逆矩阵的行列式不为零。

等角变换

● 如果变换前后两向量夹角的大小和方向都不改变，改变换是等角的。 只有平移， 旋转和均匀缩放是等角变换。 等角变换将会保持比例不变。 镜像并不是等角变换， 因为尽管两向量夹角的大小不变，但夹角的方向改变了。 所有等角变换都是仿射和可逆的。

正交变换

● 正交变换的基本思想是轴保持互相垂直， 而且不进行缩放变换。 正交变换很有意思， 因为很容易求出 它的逆

● 平移、旋转和镜像是仅有的正交变换。 长度、角度、面积和体积都保持不变。（尽管如此，但因为镜像变换被认为是正交变换，所以一定要密切注意角度、面积和体积的准确定义）。

● 所以正交矩阵都是仿射和可逆的。

刚体变换

● 刚体变换只改变物体的位置和方向， 不包括形状。 所有长度、角度、面积和体积都不变。平移和旋转是仅有的刚体变换， 镜像并不被认为是刚体变换

● 刚体变换也被称作正规变换。所以刚体变换都是正交、等角、可逆和仿射的。

● 某些刚体变换旋转矩阵的行列式为1。

最后

以上就是明理板栗为你收集整理的第8章 矩阵和线性变换的全部内容，希望文章能够帮你解决第8章 矩阵和线性变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。