图像压缩,最大子段和--以及对追踪解的一点优化
- 图像压缩
- 关于追踪解的一点优化:
- 输出样例
- 追踪解代码
- 完整程序代码
- 最大子段和
- 蛮力算法( O ( n 3 ) O(n^3) O(n3))
- 分治策略
- 对追踪解的一点点改进
- 输出演示
- 完整程序代码
- 动态规划
- 解法介绍
- 完整代码
- 优化查找前序列 O ( n ) O(n) O(n)
- 最优二叉检索树
- 介绍
- 完整代码
图像压缩
介绍引用:
计算机中的图像由一系列像素点构成,每个像素点称为一个像素,图像分辨率越高,使用的像素就越多,例如Windows桌面的图片常用的设置事1024*768个,大概到 1 0 6 10^6 106数量级。图像传输和视频处理有时在1秒钟内要处理几十帧图片,图像压缩就显得尤为重要。
- 1、问题描述:
以黑白图像的处理来说明图像处理问题,在计算机中,常用像素点的灰度值序列{p1,p1,……pn}表示图像。其中整数pi,1<=i<=n,表示像素点i的灰度值。通常灰度值的范围是0~255。因此最多需要8位表示一个像素。
压缩的原理就是把序列 { p 1 , p 2 , … … p n } {p_1,p_2,……p_n} {p1,p2,……pn}进行设断点,将其分割成一段一段的。分段的过程就是要找出断点,让一段里面的像素的最大灰度值比较小,那么这一段像素(本来需要8位)就可以用较少的位(比如7位)来表示,从而减少存储空间。
b代表bits,l代表length,分段是,b[i]表示每段一个像素点需要的最少存储空间(少于8位才有意义),l[i]表示每段里面有多少个像素点,s[i]表示从0到i压缩为一共占多少存储空间。
如果限制l[i]<=255,则需要8位来表示l[i]。而b[i]<=8,需要3位表示b[i]。所以每段所需的存储空间为l[i]*b[i]+11位。假设将原图像分成m段,那么需要位的存储空间。
图像压缩问题就是要确定像素序列{p1,p1,……pn}的最优分段,使得依此分段所需的存储空间最小。 - 2、最优子结构性质
设l[i],b[i],1<=i<=m是{p1,p1,……pn}的一个最优分段,则l[1],b[1]是{p1,……,pl[1]}的一个最优分段,且l[i],b[i],2<=i<=m是{pl[1]+1,……,pn}的一个最优分段。即图像压缩问题满足最优子结构性质。 - 3、递推关系
设s[i],1<=i<=n是像素序列{p1,p1,……pi}的最优分段所需的存储位数,则s[i]为前i-k个的存储位数加上后k个的存储空间。由最优子结构性质可得:
S [ i ] = min 1 ≤ j ≤ m i n { i , 256 } { S [ i − j ] + j ∗ b [ i − j + 1 , i ] + 11 } S[i]=displaystylemin_{1≤j≤min{i,256}}{S[i-j]+j*b[i-j+1,i]+11} S[i]=1≤j≤min{i,256}min{S[i−j]+j∗b[i−j+1,i]+11} - 4、构造最优解
数组l[i],b[i]记录了最优分段所需的信息最优分段的最后一段的段长度和像素位数分别存储在l[n]和b[n]中,其前一段的段长度和像素位数存储于l[n-l[n]]和b[n-l[n]]中,依此类推,可在O(n)时间内构造最优解。
关于追踪解的一点优化:
正序的就用队列,倒序的变成正序的就用堆栈。
学习了队列和堆栈的使用,可以用于变化顺序。当然如果是python,直接[::-1]就可逆序。
已知一个数组序列,倒序的分片方式已经获得。如何正序地输出每个分片。
把倒序的分片方式压入到一个栈中,再正序地pop()出栈的元素,即得到了正序的分片方式。
再考虑对数组进行入队出队。即可得到正序的分片的数组元素。
C++实现栈与C++实现队列(参考这篇博文学习相关的函数实现)
输出样例
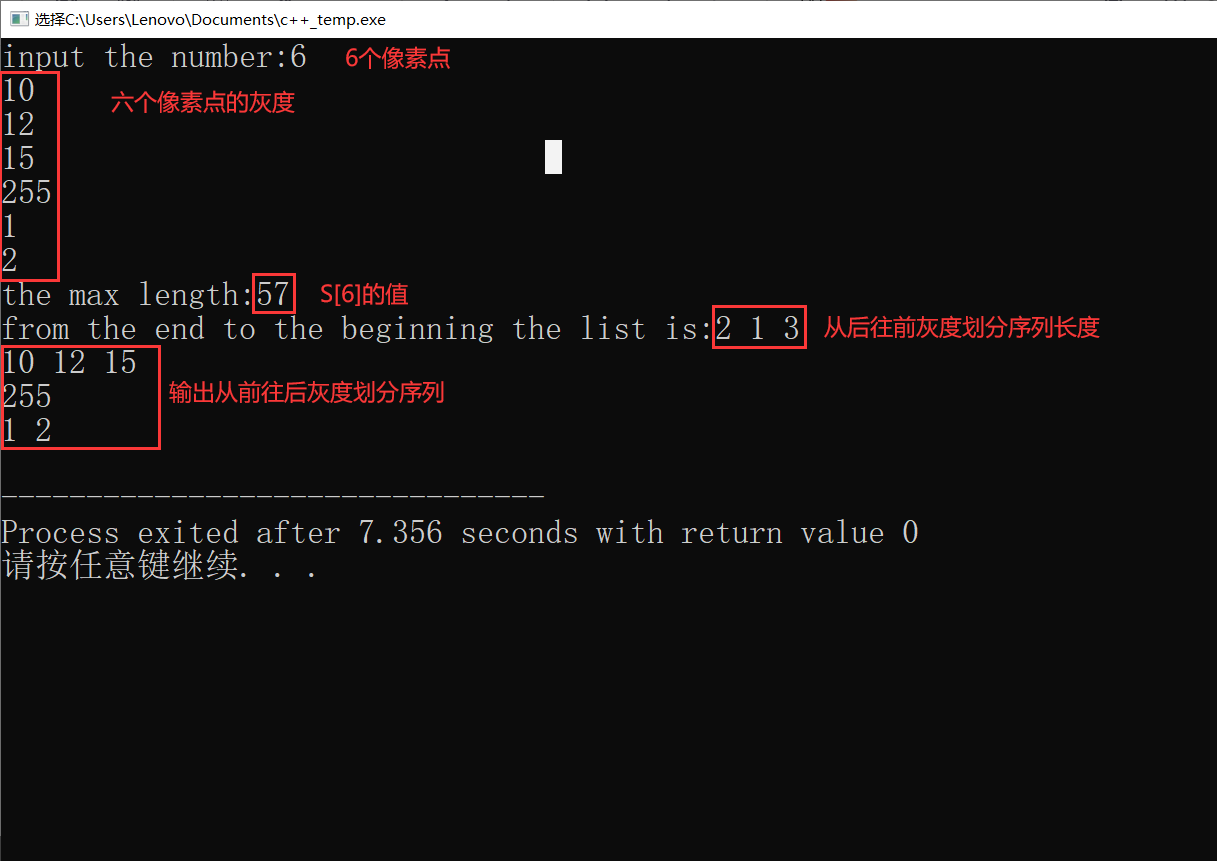
追踪解代码
void traceback(int s[],int a[],int m)//s[]为像素点灰度序列,a[]为追踪解数组,m为像素点个数。
{
int k;//k记录分为几段
stack<int> stk;//开辟一个堆栈
queue<int> q;//开辟一个队列
cout<<"from the end to the beginning the list is:";
while(a[m]>0)
{
++k;
cout<<a[m]<<" ";
stk.push(a[m]);
m-=a[m];
if(a[m]==0)
break;
}
cout<<endl;
while(!stk.empty())
{
q.push(stk.top());
stk.pop();
}
int i=1;
int tmp=q.front();//获得队首元素值
while(tmp!=0)
{
while(tmp>0)//以tmp作为循环条件,输出tmp个像素值
{
cout<<s[i]<<" ";
tmp--;
++i;
}
cout<<endl;
q.pop();
tmp=q.front();
}
}
完整程序代码
#include <queue>
#include <stack>
#include <iostream>
#include <math.h>
#include <string>
#include <stack>
using namespace std;
const int Lmax=256;
const int header=11;
void traceback(int s[],int a[],int m)
{
int k;//k记录分为几段
stack<int> stk;
queue<int> q;
cout<<"from the end to the beginning the list is:";
while(a[m]>0)
{
++k;
cout<<a[m]<<" ";
stk.push(a[m]);
m-=a[m];
if(a[m]==0)
break;
}
cout<<endl;
while(!stk.empty())
{
q.push(stk.top());
stk.pop();
}
int i=1;
int tmp=q.front();//获得队首元素值
while(tmp!=0)
{
while(tmp>0)//以tmp作为循环条件,输出tmp个像素值
{
cout<<s[i]<<" ";
tmp--;
++i;
}
cout<<endl;
q.pop();
tmp=q.front();
}
}
int binary_length(int i)//获得i的二进制长度
{
int k=0;
if(i==0) return 1;
while(i>0)
{
++k;
i=i/2;
}
return k;
}
int min(int a,int b)//返回两个数最小值
{
if(a>b)
return b;
else
return a;
}
int main()
{
int n,i,j;
cout<<"input the number:";cin>>n;
int *p=new int[n+1];//存储灰度
p[0]=0;
for(i=1;i<=n;++i)
{
cin>>p[i];
}
int S[n+1];//记录装入了i个像素的总的最小位数
int L[n+1];//记录达最少位数时最后一段的灰度值的个数
int b[n+1];//存储n个像素灰度的二进制位数
S[0]=0;L[0]=0;b[0]=0;
int bmax=0;//记录每个分段中像素灰度的上限
for(i=1;i<=n;++i)//子问题后边界
{
b[i]=binary_length(p[i]);
bmax=b[i];
S[i]=S[i-1]+bmax;
L[i]=1;
for(j=2;j<=min(i,Lmax);++j)//最后一段长
{
if(bmax<b[i-j+1])//使bmax保持最大
{
bmax=b[i-j+1];
}
if(S[i]>S[i-j]+j*bmax)//如果有更优的段长,更新S[i]和L[i]
{
S[i]=S[i-j]+j*bmax;
L[i]=j;
}
}
S[i]=S[i]+header;//每一段要加上头部
bmax=0;//对下一个新的序列,bmax归零
}
cout<<"the max length:"<<S[n]<<endl;
traceback(p,L,n);
}
最大子段和
该问题和最长子序列不一样,子段和必须要连续
蛮力算法( O ( n 3 ) O(n^3) O(n3))
三级循环,i为左边界,j为右边界,k用于遍历从i到j。
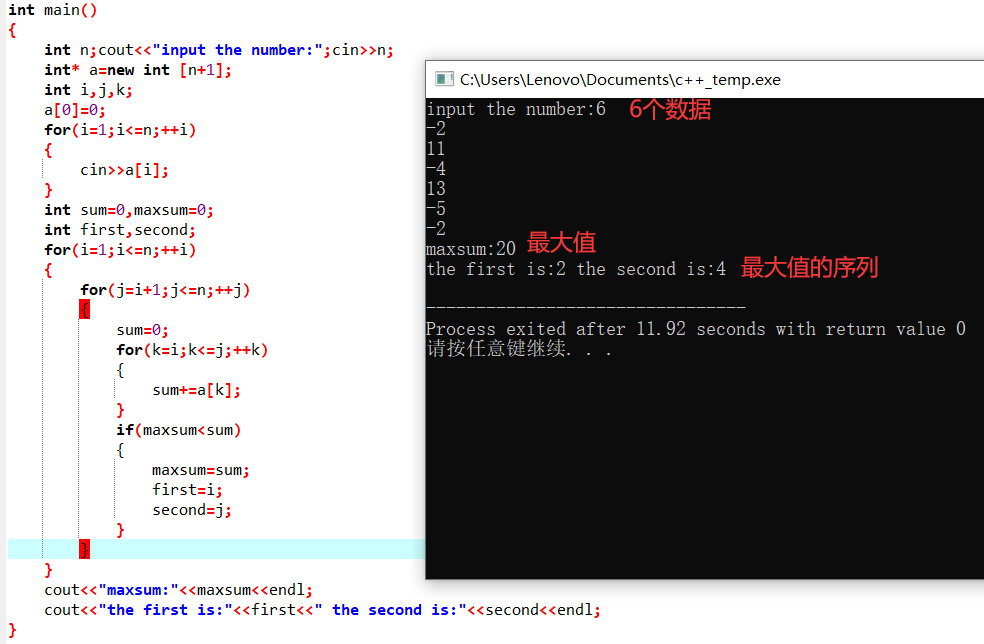
int main()
{
int n;cout<<"input the number:";cin>>n;
int* a=new int [n+1];
int i,j,k;
a[0]=0;
for(i=1;i<=n;++i)
{
cin>>a[i];//输入全部序列
}
int sum=0,maxsum=0;
int first,second;
for(i=1;i<=n;++i)//左边界
{
for(j=i+1;j<=n;++j)//右边界
{
sum=0;
for(k=i;k<=j;++k)//序列和
{
sum+=a[k];
}
if(maxsum<sum)//如果序列和大于最大值,就更新记录
{
maxsum=sum;
first=i;//记录最大和的首位置
second=j;//记最大和的末位置
}
}
}
cout<<"maxsum:"<<maxsum<<endl;
cout<<"the first is:"<<first<<" the second is:"<<second<<endl;
}
分治策略
时间复杂度分析:递归调用, T ( n ) = 2 T ( n / 2 ) + O ( n ) , T ( 1 ) = 0 T(n)=2T(n/2)+O(n),T(1)=0 T(n)=2T(n/2)+O(n),T(1)=0
解为 T ( n ) = O ( n l o g n ) T(n)=O(nlogn) T(n)=O(nlogn)
从 [ n / 2 ] [n/2] [n/2]的位置将A划分成A1和A2前后两半,第三种情况是横跨中间的子段和,需要特殊处理,向左遍历找到S1,向右遍历找到S2,加和得到S2,再与A1和A2的比较。
对追踪解的一点点改进
书中提及,要输出左右下标,简单的一句话这样描述
算法计算出子问题的最大子段和的同时也可以记录下这个和的前后边界以便最终输出时使用
然而实现起来似乎并没有那么容易。
此处博主采用的方法是额外定义两个常量,利用lsum()向左求最大值s1时记录下左最大序列下标:lflag。利用rsum()向右求最大值s2时记录下左最大序列下标:rflag,并用引用返回修改其值。(自己之前调试遇到的bug是因为没有定义这个常量,而使用end或者beg的引用,将i的值赋给他们,导致循环出现问题)
输出演示
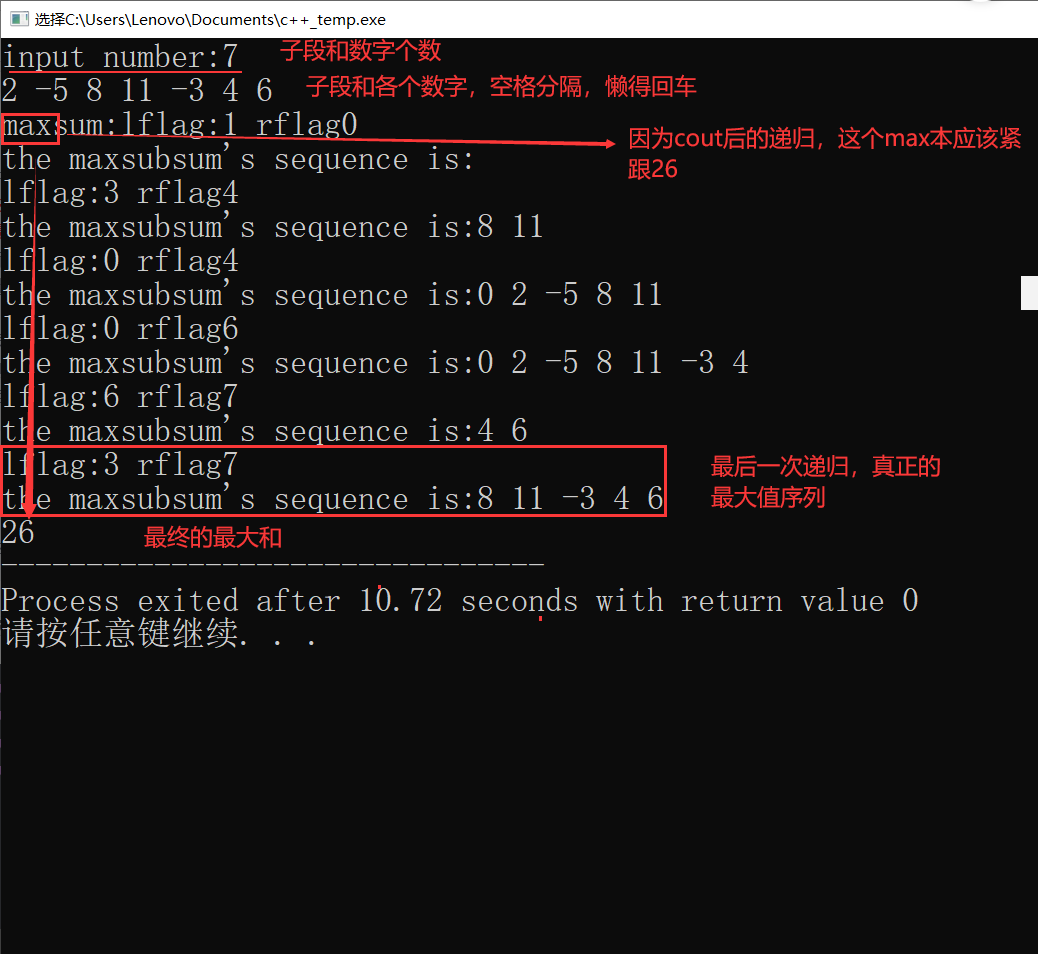
因为存在递归,所以就很难看,注意看最后一次有效的递归输出即可
8,11,-3,4,6
完整程序代码
#include <iostream>
#include <math.h>
#include <string>
#include <stack>
using namespace std;
const int leftflag=0;//记录左最大序列左下标
const int rightflag=0;//记录最大序列右下标
int max(int a,int b)//求两数种较大者的函数
{
if(a>b)
return a;
else
return b;
}
int lsum(int A[],int beg,int end,int& lflag)//给出左右下标的向左的顺序求最大和函数
{
int sum=0;
int maxsum=0;
int i;
for(i=end;i>=beg;--i)
{
sum+=A[i];
if(sum>maxsum)
{
maxsum=sum;
lflag=i;
//改值了,应该用flag beg=i;
}
}
return maxsum;
}
int rsum(int A[],int beg,int end,int& rflag)//给出左右下标的向右的顺序求最大和函数
{
int sum=0;
int maxsum=0;
int i;
for(i=beg;i<=end;++i)
{
sum+=A[i];
if(sum>maxsum)
{
maxsum=sum;
rflag=i;
//改值了,应该用flag end=i;
}
}
return maxsum;
}
int MaxSubSum(int A[],int left,int right)//A为数组,left为左下标,right为右下标
{
int i,j;
if(left==right)
{
return max(A[left],0);
}
int lflag=0,rflag=0;
int center=(left+right)/2;
int leftsum=MaxSubSum(A,left,center);//左递归
int rightsum=MaxSubSum(A,center+1,right);//右递归
int sum1=lsum(A,left,center,lflag);//第三种情况的向左探测
int sum2=rsum(A,center+1,right,rflag);//第三种情况的向右探测
int sum=sum1+sum2;
if(leftsum>sum)
{
sum=leftsum;
}
if(rightsum>sum)
{
sum=rightsum;
}
cout<<"lflag:"<<lflag<<" rflag"<<rflag<<endl;
cout<<"the maxsubsum's sequence is:";
for(int i=lflag;i<=rflag;++i)//追踪解,输出最大子列和序列
{
cout<<A[i]<<" ";
}
cout<<endl;
return sum;
}
int main()
{
int n;cout<<"input number:";cin>>n;
int* p=new int [n+1];//多定义一位,使0号数据弃置,还可以表示n号数据为p[n]
p[0]=0;//0号数据弃置
int i;
for(i=1;i<=n;++i)
{
cin>>p[i];
}
cout<<"maxsum:"<<MaxSubSum(p,1,n);
return 0;
}
动态规划
解法介绍
- 先考虑子问题的划分,一般情况下,如果能用一个参数来表示问题的边界,尽量采用一个参数,先考虑所有子问题都从A[1]开始,对于给定的i,子问题的输入是数组A[1…i],其中 1 ≤ i ≤ n 1≤i≤n 1≤i≤n。如果子问题的优化函数值C[i]表示A[1…i]的最大子段和,那么对于优化函数 C [ j ] ( j > i ) C[j](j>i) C[j](j>i)来讲,它与C[i]之间的依赖关系的确定就比较困难,因为达到最大子段和的最后一个元素不一定是A[i]。这时,就需要考虑它后面的元素的影响。
- 比如 < 2. − 5 , 8 , 11 , − 3 > <2.-5,8,11,-3> <2.−5,8,11,−3>这个序列,子段和C[5]=8+11=19,爱计算子问题A[1…6]时,不能直接把对应于A[1…5]的最优解子段<8,11>的组合进来,因为11后面还有-3,它对和也有影响。
- 因此,为了得到效率更高的算法,我们需要在子问题之间建立一个简单的递推关系,为此需要改变优化函数的定义。
定义C[i]是输入A[1…i]中必须包含A[i]的最大子段和。即
C [ i ] = max 1 ≤ k ≤ i { ∑ j = k i A [ j ] } C[i]=displaystylemax_{1≤k≤i}{displaystyle∑_{j=k}^iA[j]} C[i]=1≤k≤imax{j=k∑iA[j]}
根据定义表达式,就比较容易去思考如何写代码,i是最外层循环的终止下标,k是i下面一层循环的起始下标,j遍历的k到i,也是一个循环,这是 O ( n 3 ) O(n^3) O(n3)的复杂度,应该按递推关系写…
这样递推关系就比较容易得出来:
C
[
i
+
1
]
=
m
a
x
{
C
[
i
]
+
A
[
i
+
1
]
,
A
[
i
+
1
]
}
C[i+1]=max{C[i]+A[i+1],A[i+1]}
C[i+1]=max{C[i]+A[i+1],A[i+1]}也即A[i+1]是必须的,按照新规定的优化函数定义,取最大就是C[i]是否为正值。
C[1]=A[1],若A[1]>0,否则C[1]=0
A[1…n]是一个输入数组,C[i]就是一个循环。附加判断
完整代码
#include <iostream>
using namespace std;
int max2(int a,int b)
{
if(a>b)
return a;
else
return b;
}
int main()
{
int n;cout<<"input the number:";cin>>n;
int* a=new int [n+1];
a[0]=0;
int i;
for(i=1;i<=n;++i)
{
cin>>a[i];
}
int c[n+1]={0};
if(a[1]>0)
c[1]=a[1];
else
c[1]=0;
int end=0;
for(i=1;i<n;++i)
{
//c[i+1]=max(c[i]+a[i+1],a[i+1]);//通过max就无法记录最大值的最后下标,也是个弊端
if(c[i]>0)
{
c[i+1]=c[i]+a[i+1];
end=i+1;
}
else
{
end=i+1;
c[i+1]=a[i+1];
}
}
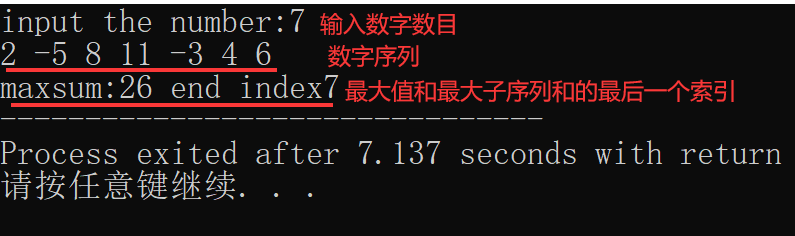
cout<<"maxsum:"<<c[n]<<" end index"<<end;
}
优化查找前序列 O ( n ) O(n) O(n)
书上又说
算法的输出是最大子段和的值sum和子段的最后位置,子段的起始位置怎样确定呢?这还需要一点额外的工作,计算时间不超过 O ( n ) O(n) O(n),请读者考虑怎样做。
end=i+1,实际上也是beg=i+1。因为如果c[i]<0,那么意味着前面的子段和都要抛弃,新的子段和从单独一个元素a[i+1]开始,起始下标和终止下标都要更新。
#include <iostream>
using namespace std;
int main()
{
int n;cout<<"input the number:";cin>>n;
int* a=new int [n+1];
a[0]=0;
int i;
for(i=1;i<=n;++i)
{
cin>>a[i];
}
int c[n+1]={0};
if(a[1]>0)
c[1]=a[1];
else
c[1]=0;
int end=0;
int beg=1;//子段本从a[1]开始
for(i=1;i<n;++i)
{
if(c[i]>0)
{
c[i+1]=c[i]+a[i+1];
end=i+1;
}
else//如果c[i]<0,那么意味着前面的子段和都要抛弃,新的子段和从单独一个元素a[i+1]开始。
{
beg=i+1;//更新beg和end
end=i+1;
c[i+1]=a[i+1];
}
}
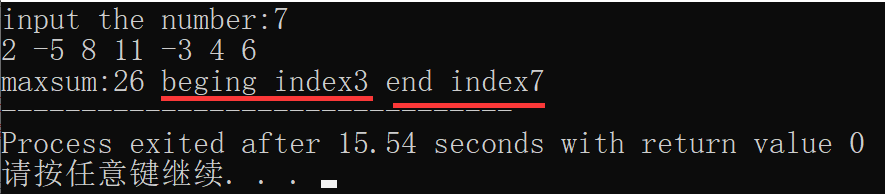
cout<<"maxsum:"<<c[n]<<" beging index"<<beg<<" end index"<<end;
}
最优二叉检索树
介绍
- 有数据集
S和空隙集L:L0表示小于1的空隙,L1表示1和2之间的空隙。
查找x,如果x属于S,那么在二叉树中的比较次数就是x在树中的深度加1,如果x不属于S,算法执行的比较次数就是x对应的空隙结点的深度。
注意根深度为0,从0开始 - 设 S = < x 1 , x 2 , . . . , x n > S=<x_1,x_2,...,x_n> S=<x1,x2,...,xn>是数据集,称 ( − ∞ , x 1 ) , ( x 1 , x 2 ) , . , . . , ( x n − 1 , x n ) , ( x n , + ∞ ) (-∞,x_1),(x_1,x_2),.,..,(x_{n-1},x_n),(x_n,+∞) (−∞,x1),(x1,x2),.,..,(xn−1,xn),(xn,+∞)为第0个,第1…第n个空隙,分别记作 L 0 , L 1 , . . . , L n L_0,L_1,...,L_n L0,L1,...,Ln。假x处在x1的概率是bi(i=1,2,…n),处在第j(j=0,1,2…n)个空隙的概率是aj。那么与S相关的存取概率分布是 P = < a 0 , b 1 , a 1 , b 2 , . . . , a i , b i + 1 , . . . , b n , a n > P=<a_0,b_1,a_1,b_2,...,a_i,b_i+1,...,b_n,a_n> P=<a0,b1,a1,b2,...,ai,bi+1,...,bn,an>。可以看出空隙结点的概率恰好比数据结点的概率多1。
- T是S的一棵二分检索树,结点 x i x_i xi在T中的深度是 d ( x i ) d(x_i) d(xi),i=1,2,…,n空隙 L j L_j Lj的深度为 d ( L j ) d(L_j) d(Lj),j=0,1,…,n,则平均比较次数为
- t = ∑ i = 1 n b i ( 1 + d ( x i ) ) + ∑ j = 0 n a j d ( L j ) t=displaystyle∑_{i=1}^nb_i(1+d(x_i))+∑_{j=0}^na_jd(L_j) t=i=1∑nbi(1+d(xi))+j=0∑najd(Lj)
- 目标:给定n个结点,构造一棵二叉检索树,使得检索的代价最低,即最优二叉检索树。
- 利用动态规划的思想解决这个问题,我们首先要找到能划分的子问题,即节点减少时的二叉检索树。因此最优二叉检索树一定具有最优子结构的特征,去除根节点的剩下的部分任然是最优二叉检索树。
- 预选定 x k x_k xk作为根, k = i , i + 1 , . . . j k=i,i+1,...j k=i,i+1,...j,原来的S[i,j]被划分为S[i,k-1]和S[k+1,j]两个更小的子集。如果T[i,j]是一棵关于S[i,j]和存取概率分布P[i,j]的一棵最优二分检索树,可证明满足优化原则。注意在k=i的情况下,子问题S[i,i-1]不含有数据,相对应的概率分布只含有一个空隙概率 a i − 1 a_{i-1} ai−1,这意味着构造的子树只含有一个空隙结点。如狗查找的x恰好位于这个空隙结点,那么它将在与父节点 x i x_i xi的比较中被确认,在这棵子树内不需要做进一步比较,于是对该子树的平均检索次数应该等于0.同样的,对于k=j的情况也有类似结果。这两种情况都对应于该空数据集的最小子问题,相应的优化函数的递推关系应该在这里取得初值,即当问题规模为0时(含0个数据结点的子问题)时,比较次数等于0.
- 假设
m
(
i
,
j
)
m(i,j)
m(i,j)是相对输入S[i,j]和P[i,j]的最优二分检索树的平均比较次数。
令 ω [ i , j ] = ∑ p = i − 1 j a p + ∑ q = i j b q ω[i,j]=displaystyle∑_{p=i-1}^ja_p+displaystyle∑_{q=i}^jb_q ω[i,j]=p=i−1∑jap+q=i∑jbq是P[i,j]中的所有概率(包括元素与空隙之和) - m ( i , j ) m(i,j) m(i,j)包含 i … j i…j i…j节点的数的搜索代价,设这棵树的根节点为r,对应的左右子树分别是 i … r − 1 i…r-1 i…r−1和 r + 1 , … , j r+1,…,j r+1,…,j,它们对应的叶子分别为 i − 1 … d r − 1 i-1…dr-1 i−1…dr−1和 r … j r…j r…j。树就构造完了,分为两种情况:
- 只有一个叶子组成的子树 j=i-1,只有i-1,那么 m ( i , j ) = q i − 1 m(i,j)=qi−1 m(i,j)=qi−1 这个子树为1个叶节点 不再划分左右子树;
- 子树还包含关键字 即继续划分左右子树。那么
m ( i , j ) = min i ≤ k ≤ j [ m ( i , k − 1 ) + m ( k + 1 , j ) + w ( i , j ) ] , 1 ≤ i ≤ j ≤ n m(i,j) = displaystylemin_{i≤k≤j}[m(i,k-1)+m(k+1,j)+w(i,j)],1≤i≤j≤n m(i,j)=i≤k≤jmin[m(i,k−1)+m(k+1,j)+w(i,j)],1≤i≤j≤n
m [ i , i − 1 ] = 0 , i = 1 , 2 , . . . , n m[i,i-1]=0,i=1,2,...,n m[i,i−1]=0,i=1,2,...,n
以r为根的代价中最小值,即最优二叉检索树。
捣鼓了半天vscode。
会提示问题所在,很方便。
Visual Studio Code 如何编写运行 C、C++ 程序?
设断点,调式代码还有待学习,不过程序这下运行成功了。
完整代码
这里测的给定输入是:
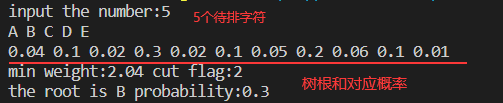
S = < A , B , C , D , E > S=<A,B,C,D,E> S=<A,B,C,D,E>
P = < 0.04 , 0.1 , 0.02 , 0.3 , 0.02 , 0.1 , 0.05 , 0.2 , 0.06 , 0.1 , 0.01 > P=<0.04,0.1,0.02,0.3,0.02,0.1,0.05,0.2,0.06,0.1,0.01> P=<0.04,0.1,0.02,0.3,0.02,0.1,0.05,0.2,0.06,0.1,0.01>
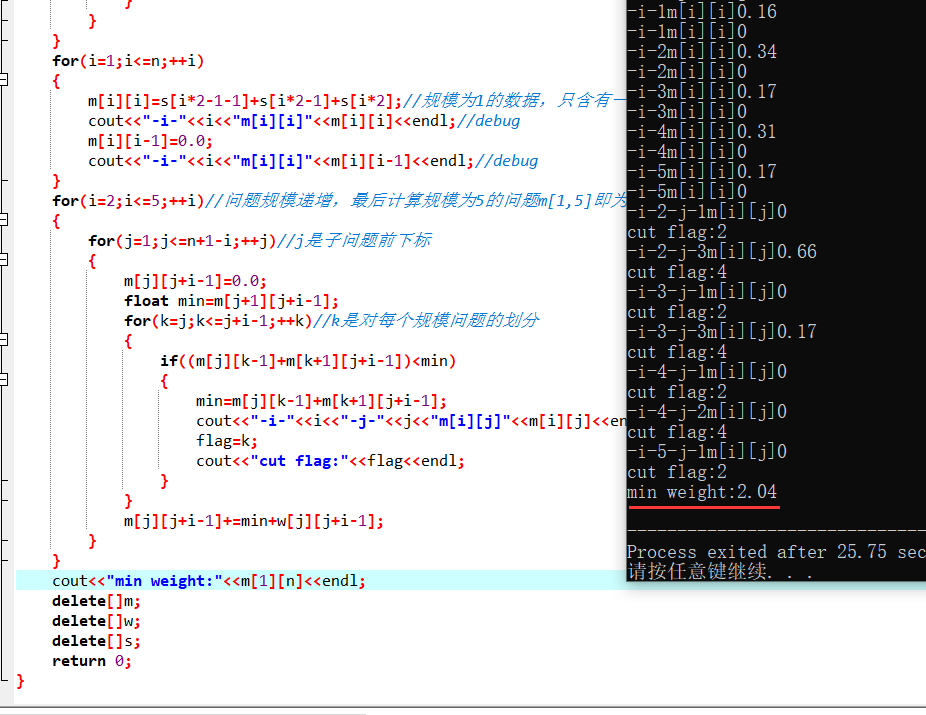
可以最优二叉树的平均比较次数是2.04次,根的cut位置是2,也即对应于0.3概率的数据:B
/*
* @Description: 5
* @Autor: dive668
* @Date: 2021-04-30 11:15:30
* @LastEditors: dive668
* @LastEditTime: 2021-04-30 11:37:10
*/
#include <iostream>
using namespace std;
int main()
{
int n;cout<<"input the number:";cin>>n;//结点数为n,但概率总数为2*n+1,包含n+1个空隙的概率。
char c[n + 1]={"0"};
float* s=new float[2*n+1];
int i,j,k;
int flag=0;//记录最下划分k的值
for (i = 1; i <= n;++i)//输入字母序列
{
cin >> c[i];
}
for (i = 0; i <= 2 * n; ++i) //输入数据概率和空隙概率交叉序列
{
cin >> s[i];
}
float m[n+1][n+1]={0.0};
float w[n+1][n+1]={0.0};
for(i=1;i<=n;++i)//i是起始下标
{
for(j=i;j<=n;++j)//j是终止下标
{
w[i][j]=s[2*(i-1)];//因为w[i][j]的空隙概率比数据概率多一个,所以先初始化为一个空隙概率
}
}
for(i=1;i<=n;++i)
{
for(j=i;j<=n;++j)
{
for(k=i;k<=j;++k)
{
w[i][j]+=s[2*k-1]+s[2*k];
}
}
}
for(i=1;i<=n;++i)
{
m[i][i]=s[i*2-1-1]+s[i*2-1]+s[i*2];//规模为1的数据,只含有一个结点的子问题
m[i][i-1]=0.0;
}
for(i=2;i<=5;++i)//问题规模递增,最后计算规模为5的问题m[1,5]即为问题的解
{
for(j=1;j<=n+1-i;++j)//j是子问题前下标
{
m[j][j+i-1]=0.0;
float min=m[j+1][j+i-1];
for(k=j;k<=j+i-1;++k)//k是对每个规模问题的划分
{
if((m[j][k-1]+m[k+1][j+i-1])<min)
{
min=m[j][k-1]+m[k+1][j+i-1];
flag=k;
}
}
m[j][j+i-1]+=min+w[j][j+i-1];
}
}
cout<<"min weight:"<<m[1][n]<<" cut flag:"<<flag<<endl;
cout<<"the root is "<<c[flag]<<" probability:"<<s[2*flag-1];
delete []s;
return 0;
}
最后
以上就是悲凉香烟最近收集整理的关于【动态规划】(下)图像压缩,最大子段和,最优二分检索树--以及对追踪解的一点优化的全部内容,更多相关【动态规划】(下)图像压缩,最大子段和,最优二分检索树--以及对追踪解内容请搜索靠谱客的其他文章。








发表评论 取消回复