Day15--Simulink自定义功能模块

该系列博客主要讲述Matlab软件在自动控制方面的应用，如无自动控制理论基础，请先学习自动控制系列博文，该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接：https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍：《MATLAB/Simulink与控制系统仿真》。

3.系统模型转换及连接和线性化

3.1 系统模型转换及连接

3.1.1 模型转换

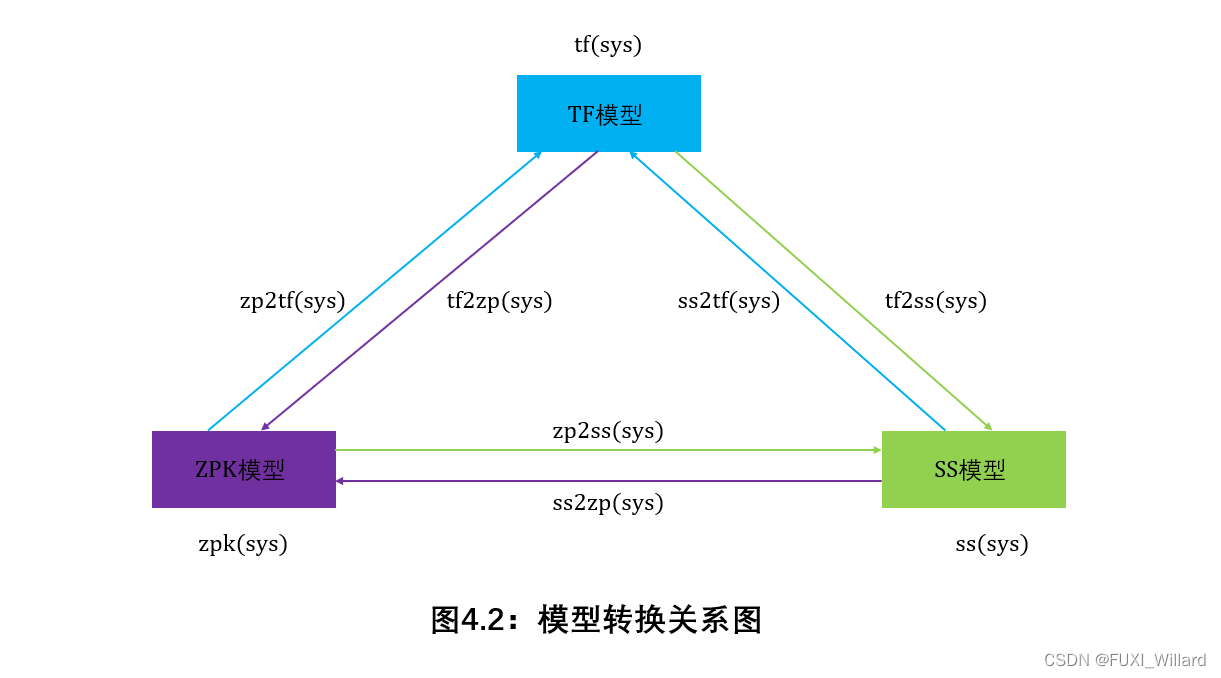
• 线性时不变系统的模型包括：传递函数$(\mathrm{Transfer}\mathrm{Function})$模型、零极点增益$(\mathrm{ZPK})$模型、状态空间$(\mathrm{State}\mathrm{Space})$模型；

• 不同模型的转换关系：

  

• 模型转换函数：

  函数名	功能描述	函数名	功能描述
  $ss2tf$	$状态空间模型转换为传递函数模型$	$tf2ss$	$传递函数模型转换为状态空间模型$
  $ss2zp$	$状态空间模型转换为零极点模型$	$zp2ss$	$零极点模型转换为状态空间模型$
  $tf2zp$	$传递函数模型转换为零极点模型$	$zp2tf$	$零极点模型转换为传递函数模型$

3.1.2 模型转换实例

实验要求：已知系统的零极点模型为：$G(s)=\frac{6(s+2)}{(s+1)(s+3)(s+5)}$，求系统对应的传递函数模型和状态空间模型。

解：

% 实例Chapter4.3 3.1.2
clc;clear;

% 系统的零点向量、极点向量和增益
z=[-2];p=[-1,-3,-5];k=6;

% 将零极点模型转换为传递函数模型
[num,den]=zp2tf(z,p,k);

% 将零极点模型转换为状态空间模型
[A,B,C,D]=zp2ss(z,p,k);

% 建立零极点模型
g_zpk=zpk(z,p,k);

% 建立传递函数模型
g_tf=tf(num,den);

% 建立状态空间模型
g_ss=ss(A,B,C,D);

% 显示不同模型
g_zpk,g_tf,g_ss

% 显示结果
% 零极点模型
g_zpk = 
       6 (s+2)
  -----------------
  (s+1) (s+3) (s+5) 
Continuous-time zero/pole/gain model.

% 传递函数模型
g_tf =
         6 s + 12
  -----------------------
  s^3 + 9 s^2 + 23 s + 15 
Continuous-time transfer function.

% 状态空间模型
g_ss = 
  A = 
           x1      x2      x3
   x1      -1       0       0
   x2       1      -8  -3.873
   x3       0   3.873       0
 
  B = 
       u1
   x1   1
   x2   1
   x3   0
 
  C = 
          x1     x2     x3
   y1      0      0  1.549
 
  D = 
       u1
   y1   0 
Continuous-time state-space model.

• 系统传递函数模型为：$G(s)=\frac{6s+12}{s^3+9s^2+23s+15}$；

• 系统状态空间模型为：
  $$\{\begin{array}{ll}& \dot{x}=\left[\begin{array}{ccc}-1& 0& 0\\ 1& -8& -3.873\\ 0& 3.873& 0\end{array}\right]x+\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]u\\ & \\ & y=\left[\begin{array}{ccc}0& 0& 1.549\end{array}\right]x\end{array}$$

3.1.3 模型连接

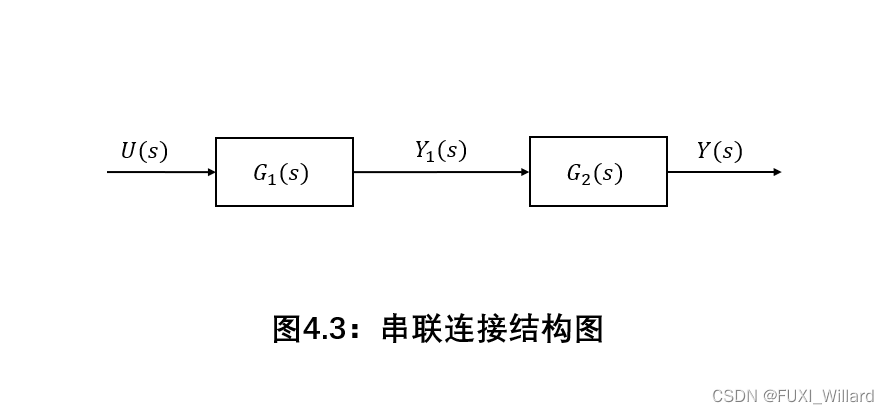
1. 串联连接

   • 单输入单输出$(\mathrm{SISO})$系统$G_1(s)$和$G_2(s)$串联连接结构图：

     

   • 串联连接合成的系统传递函数为：$G(s)=G_1(s)\cdot G_2(s)$；

   • 推广：若$n$个环节串联，则合成的传递函数为：$G(s)=G_1(s)\cdot G_2(s)\cdot \cdots \cdot G_n(s)$；

   • $\mathrm{MATLAB}$的串联函数$\mathrm{series}$：

     # 语法格式：
     [num,den]=series(num1,den1,num2,den2)
     
     # 参数说明：
     num：串联后系统的分子多项式；
     den：串联后系统的分母多项式；
     num1、num2：串联的分子多项式；
     den1、den2：串联的分母多项式；
     

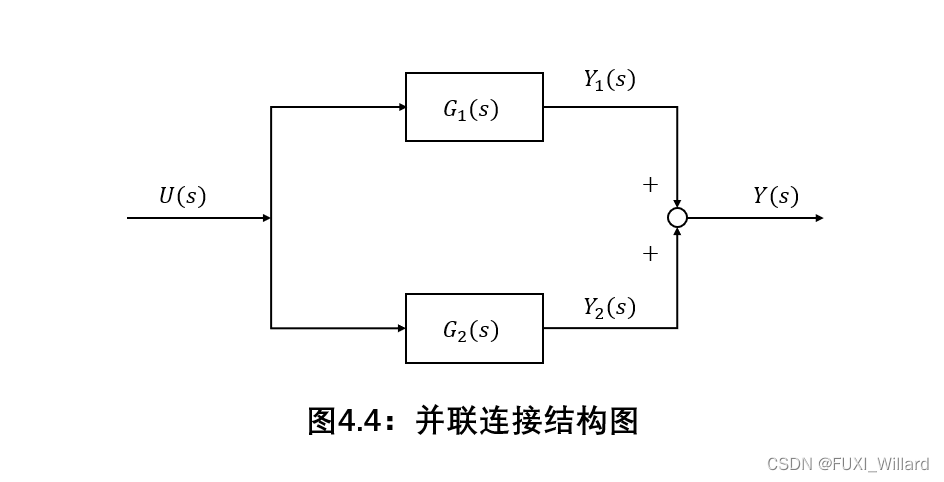
2. 并联连接

   • 单输入单输出$(\mathrm{SISO})$系统$G_1(s)$和$G_2(s)$并联连接结构图：

     

   • 并联连接合成的系统传递函数为：$G(s)=G_1(s)+G_2(s)$；

   • 推广：若$n$个环节串联，则合成的传递函数为：$G(s)=G_1(s)+G_2(s)+\cdots +G_n(s)$；

   • $\mathrm{MATLAB}$的并联函数$\mathrm{parallel}$：

     # 语法格式：
     [num,den]=parallel(num1,den1,num2,den2)
     
     # 参数说明：
     num：并联后系统的分子多项式；
     den：并联后系统的分母多项式；
     num1、num2：并联的分子多项式；
     den1、den2：并联的分母多项式；
     

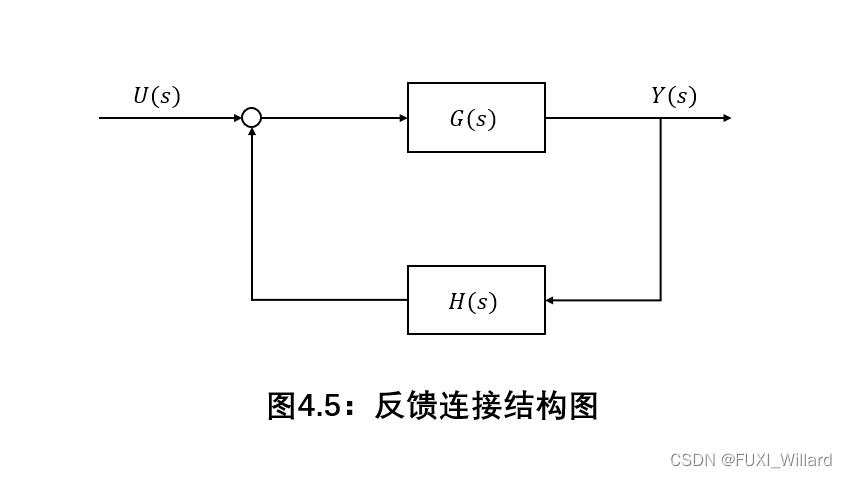
3. 反馈连接

   • 反馈系统结构图：

     

   • 当系统正反馈连接时，合成的系统传递函数为：$GH(s)=\frac{G(s)H(s)}{1-G(s)H(s)}$；

   • 当系统负反馈连接时，合成的系统传递函数为：$GH(s)=\frac{G(s)H(s)}{1+G(s)H(s)}$；

   • $\mathrm{MATLAB}$的反馈函数$\mathrm{feedback}$：

     # 语法格式：
     [num,den]=feedback(num1,den1,num2,den2,sign)
     
     # 参数说明：
     num：反馈连接后系统的分子多项式；
     den：反馈连接后系统的分母多项式；
     num1：G(s)的分子多项式；
     den1：G(s)的分母多项式；
     num2：H(s)的分子多项式；
     den2：H(s)的分母多项式；
     sign：反馈的符号，默认为负值，即sign=-1；
     

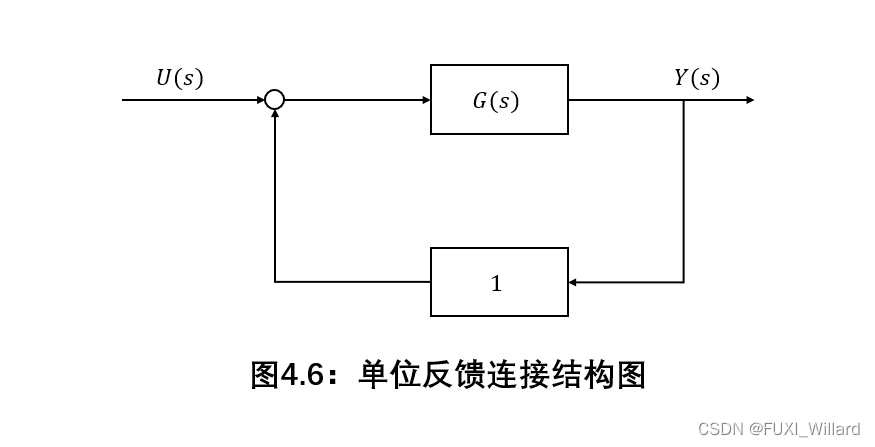
4. 单位反馈(闭环连接)

   • 单位反馈系统结构图：

     

   • $\mathrm{MATLAB}$的单位反馈函数$\mathrm{cloop}$：

     # 语法格式：
     [numc,denc]=cloop(num,den,sign)
     
     # 参数说明：
     numc：单位反馈连接后系统的分子多项式；
     denc：单位反馈连接后系统的分母多项式；
     num：G(s)的分子多项式；
     den：G(s)的分母多项式；
     sign：反馈的符号，默认为负值，即sign=-1；
     sign=1，采用正反馈；sign=-1，采用负反馈；
     

3.1.4 模型串并连连接实例

实验要求：已知两系统的传递函数：$G_1(s)=\frac{6(s+2)}{(s+1)(s+3)(s+5)}、G_1(s)=\frac{(s+2.5)}{(s+1)(s+4)}$，求系统串联、并联的传递函数。

解：

% 实例Chapter4.3 3.1.4
clc;clear;

% 建立两系统的分子分母行向量
% 系统1
num1=6*[1,2];den1=conv([1,1],conv([1,3],[1,5]));

% 系统2
num2=[1,2.5];den2=conv([1,1],[1,4]);

% 系统串联连接
[nums,dens]=series(num1,den1,num2,den2);

% 系统并联连接
[nump,denp]=parallel(num1,den1,num2,den2);

% 建立串联和并联后模型
s_tf=tf(nums,dens);
p_tf=tf(nump,denp);

% 显示串联后和并联后模型
s_tf,p_tf

% 结果显示：
% 串联模型
s_tf = 
               6 s^2 + 27 s + 30
  --------------------------------------------
  s^5 + 14 s^4 + 72 s^3 + 166 s^2 + 167 s + 60
 
Continuous-time transfer function.

% 并联模型
p_tf = 
   s^4 + 17.5 s^3 + 87.5 s^2 + 156.5 s + 85.5
  --------------------------------------------
  s^5 + 14 s^4 + 72 s^3 + 166 s^2 + 167 s + 60
 
Continuous-time transfer function.

• 串联后系统传递函数为：$G(s)=\frac{6s^2+27s+30}{s^5+14s^4+72s^3+166s^2+167s+60}$；
• 并联后系统传递函数为：$G(s)=\frac{s^4+17.5s^3+87.5s^2+156.5s+85.5}{s^5+14s^4+72s^3+166s^2+167s+60}$；

3.1.5 模型反馈连接实例

实验要求：已知系统的前向传递函数为：$G(s)=\frac{s-1}{s^2-5s-2}$，分别求解反馈传递函数为：$H(s)=1、$$H(s)=\frac{s+1}{s^2+3s+2}$时闭环连接传递函数(单位反馈)和负反馈传递函数。

解：

% 实例Chapter4.3 3.1.5
clc;clear;

% 前向传递函数分子分母多项式系数向量
num=[1,-1];den=[1,-5,-2];

% 反馈传递函数的分子分母多项式系数向量
numh=[1,1];denh=[1,3,2];

% 闭环连接(单位反馈)
[numc,denc]=cloop(num,den);

% 反馈连接
[numf,denf]=feedback(num,den,numh,denh);

% 闭环传递函数和反馈连接传递函数
c_tf=tf(numc,denc);
f_tf=tf(numf,denf);

% 显示模型
c_tf,f_tf

% 结果显示：
% 闭环连接(单位反馈)模型
c_tf = 
      s - 1
  -------------
  s^2 - 4 s - 3 
Continuous-time transfer function.

% 反馈连接模型
f_tf = 
        s^3 + 2 s^2 - s - 2
  -------------------------------
  s^4 - 2 s^3 - 14 s^2 - 16 s - 5 
Continuous-time transfer function.

• 闭环连接(单位反馈)模型：$G(s)=\frac{s-1}{s^2-4s-3}$；
• 反馈连接模型：$G(s)=\frac{s^3+2s^2-s-2}{s^4-2s^3-14s^2-16s-5}$；

3.2 非线性数学模型的线性化

3.2.1 一个自变量的线性化过程

• 控制工程中，如果系统的运行是围绕平衡点进行的，且系统中的信号是围绕平衡点变化的小信号，则可以用线性系统去近似非线性系统；这种线性系统在有限的工作范围内等效于原来的非线性系统；

• 线性化过程用数学方法描述：将一个非线性函数$y=f(x)$，在其工作点$(x_0,y_0)$处展开成泰勒级数，忽略二次以上的高阶项，可得其线性化方程，以此代替原来的非线性函数；

• 因为忽略了泰勒级数展开中的高阶项，因此，这些被忽略的项必须很小，即变量只能对工作状态有微小的偏离；

• 对于具有一个自变量的非线性函数，设输入量为$x(t)$，输出量为$y(t)$，系统正常工作点为$y_0=f(x_0)$，在$y_0=f(x_0)$附近展开成泰勒级数为：
  $$y=f(x_0)+{\left(\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right)}_{x=x_0}(x-x_0)+\frac{1}{2!}{\left(\frac{{\mathrm{d}}^{2}f(x)}{\mathrm{d}{x}^2}\right)}_{x=x_0}(x-x_0{)}^2+\cdots$$
  如果变量的变化$x-x_0$很小，则可以忽略二次以上的项，可线性化为：
  $$y=f(x_0)+{\left(\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right)}_{x=x_0}(x-x_0)\Rightarrow y=y_0+K(x-x_0)$$
  其中：$y_0=f(x_0)，K={\left(\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right)}_{x=x_0}$；

3.2.2 多输入量函数的线性化过程

• 两个输入变量的函数$y=f(x_1,x_2)$在工作点$x_1=x_{10}，x_2=x_{20}$处的线性化；

• 方程$y=f(x_1,x_2)$在工作点附近展开成泰勒级数，有：
  $$\begin{array}{rl}y& =f(x_{10},x_{20})+\left[\left(\frac{\partial f}{\partial x_1}\right)(x_1-x_{10})+\left(\frac{\partial f}{\partial x_2}\right)(x_2-x_{20})\right]\\ & \\ & +\frac{1}{2!}\left[\left(\frac{{\partial }^{2}f}{\partial x_1^2}\right)(x_1-x_{10}{)}^2+2\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)(x_1-x_{10})(x_2-x_{20})+\left(\frac{{\partial }^{2}f}{\partial x_2^2}\right)(x_2-x_{20}{)}^2\right]+\cdots \end{array}$$
  在工作点附近，高阶项忽略不计，可得：
  $$y=f(x_{10},x_{20})+{\left(\frac{\partial f}{\partial x_1}\right)}_{x=x_{10}}(x_1-x_{10})+{\left(\frac{\partial f}{\partial x_2}\right)}_{x=x_{20}}(x_2-x_{20})$$
  简化可得：
  $$y=y_0+K_1(x_1-x_{10})+K_2(x_2-x_{20})$$
  其中：$K_1={\left(\frac{\partial f}{\partial x_1}\right)}_{x=x_{10},x_2=x_{20}},K_2={\left(\frac{\partial f}{\partial x_2}\right)}_{x=x_{10},x_2=x_{20}}$；

最后

以上就是饱满柚子最近收集整理的关于Day15--Simulink自定义功能模块的全部内容，更多相关Day15--Simulink自定义功能模块内容请搜索靠谱客的其他文章。