pgm概率图模型_概率图形模型（PGM）算法| 机器学习

128 阅读 0 评论 85 点赞

我是靠谱客的博主包容早晨，最近开发中收集的这篇文章主要介绍pgm概率图模型_概率图形模型（PGM）算法| 机器学习，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

pgm概率图模型

什么是PGM？ (What is PGM?)

So, what exactly the PGM is? P → Probabilistic, G → Graphic, M → Models

那么，PGM到底是什么？ P →概率， G →图形， M →模型

概率论 (Probabilistic)

The nature of the problem that we are generally interested to solve or the type of queries interested to solve or the type of queries we want to make is all probabilistic because of uncertainty. There are many reasons that contribute to it.

由于不确定性，我们通常要解决的问题的性质，要解决的查询的类型或我们要进行的查询的类型都是概率性的。造成这种情况的原因很多。

Incomplete knowledge
不完整的知识
Noisy observation
嘈杂的观察
Some Attributes that contribute to the problem that counts and has not present in the model
导致模型中存在但尚未出现的问题的某些属性

图形化 (Graphical)

It helps us to visualize better and we use graph theory to reduce the number of relevant combinations of all the participating variables to represent the high dimensional probability distribution model more compactly.

它有助于我们更好地可视化，并且我们使用图论来减少所有参与变量的相关组合的数量，以更紧凑地表示高维概率分布模型。

模型 (Model)

A model is a declarative (means declare and defined not derived either by a domain expert by using their domain knowledge and by using statistical knowledge and learning algorithms with historical datasets) representation of a real-world scenario or a problem that we want to analyze. It is represented by using mathematical tools like graph or simple by an equation.

模型是现实情况或我们要分析的问题的声明性表示(领域专家通过使用其领域知识以及通过使用统计知识和具有历史数据集的学习算法来声明和定义的方法)。它可以通过使用数学工具(例如图形)或通过方程式来表示。

铂族金属 (PGM)

It is a technique of closely representing a joint distribution (a rich framework for encoding probability distributions over complex domains) by exploiting dependencies between the random variables. They are used to create a model for real-world scenarios and represent them in the compact graphical representation. It is also allowing us to do inference on joint distribution in a computationally cheaper way than the traditional methods. You can achieve in one line what you would traditionally ways to solve. This is in itself is very abstract and involves many terms that need its own speaks.

它是一种通过利用随机变量之间的依赖关系来紧密表示联合分布(一种用于在复杂域上编码概率分布的丰富框架)的技术。它们用于为实际场景创建模型，并以紧凑的图形表示形式表示它们。这也使我们能够以比传统方法便宜的计算方式对联合分布进行推断。您可以一站式完成传统上要解决的问题。这本身是非常抽象的，涉及许多需要自己讲话的术语。

Representations are done at the intersection of statistics and computer science. It relies on ideas of probability theory, graph algorithms, machine learning. It has a wide variety of applications Like medical diagnosis, image understanding, speech recognition, NLP, and many more. They are also an initial tool in conveying ML problems.

表示法是在统计学和计算机科学的交叉点完成的。它依赖于概率论，图算法，机器学习的思想。它具有广泛的应用程序，例如医学诊断，图像理解，语音识别，NLP等。它们还是传达机器学习问题的初始工具。

Whether the graph is directed or undirected, it classifies graphical modes into two ways — Bayesian networks and Markov networks. By knowing the PGMs algorithm we can easily understand what is Bayesian network, graphical model and Markov’s field model.

无论图形是有向的还是无向的，它都将图形模式分为两种方式-贝叶斯网络和马尔可夫网络。通过了解PGMs算法，我们可以轻松地了解什么是贝叶斯网络，图形模型和Markov场模型。

DIA. Example of probability:

DIA。 概率示例：

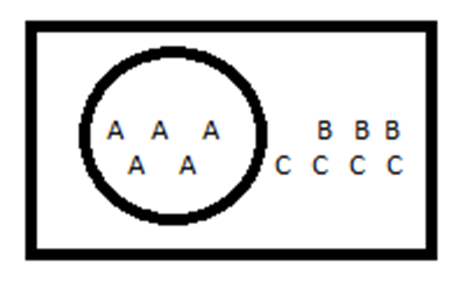
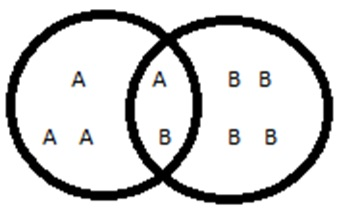
DIA. Example of Conditional Probability:

DIA。 条件概率示例：

Different kinds of distribution:

不同种类的分布：

Joint distribution: It describes how two or more variables are distributed simultaneously. To get a probability from the joint distribution of A and B, you would consider P(A=a and B=b).
联合分配：描述如何同时分配两个或多个变量。为了从A和B的联合分布中获得概率，可以考虑P(A = a和B = b) 。
Probability distribution: Conditional probability distribution looks at how the probabilities of A are distributed, given a certain value, say, for B, P(A=a | B=b).
概率分布：条件概率分布着眼于给定一定的值(例如，对于B) ， A的概率如何分布，即P(A = a | B = b) 。
Marginal distribution: It is one that results from taking a mean over one variable to get the probability distribution of the other. Like: the marginal probability distribution of A and B are related would be given by the following:
边际分布：这是对一个变量取均值以获得另一个变量的概率分布的结果。像： A和B的边际概率分布相关，将由以下公式给出：

∫^B P(a│b)P(b)db
∫ ^乙 P(a│b)P(B)分贝

Conclusion:

结论：

In this article, we have learned what is PGM with example and its different kinds of distribution? We will learn more about ML in the upcoming article. Have a nice day! Happy learning!

在本文中，我们通过示例及其不同类型的分布了解了PGM是什么？ 我们将在下一篇文章中了解有关ML的更多信息。祝你今天愉快！学习愉快！