统计推断(九) Graphical models

1. Undirected graphical models(Markov random fields)

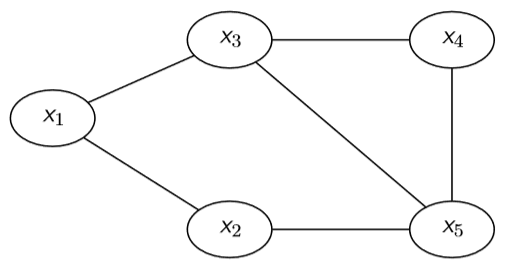
• 节点表示随机变量，边表示与节点相关的势函数
  $$p_{\mathbf{x}}(\mathbf{x})\propto {\phi }_{12}\left(x_1,x_2\right){\phi }_{13}\left(x_1,x_3\right){\phi }_{25}\left(x_2,x_5\right){\phi }_{345}\left(x_3,x_4,x_5\right)$$
  

• clique：全连接的节点集合

• maximal clique：不是其他 clique 的真子集

**Theorem (Hammersley-Clifford) **: A strictly positive distribution $p_{\mathsf{x}}(\mathbf{x})>0$ satisfies the graph separation property of undirected graphical models if and only if it can be represented in the factorized form
$$p_{\mathsf{x}}(\mathbf{x})\propto \prod _{\mathcal{A}\in \mathcal{C}}{\psi }_{{\mathbf{x}}_{\mathcal{A}}}\left({\mathbf{x}}_{\mathcal{A}}\right)$$

• conditional independence：${\mathbf{x}}_{{\mathcal{A}}_1}\perp {\mathbf{x}}_{{\mathcal{A}}_2}|{\mathbf{x}}_{{\mathcal{A}}_3}$

2. Directed graphical models(Bayesian network)

• 节点表示随机变量，有向边表示条件关系
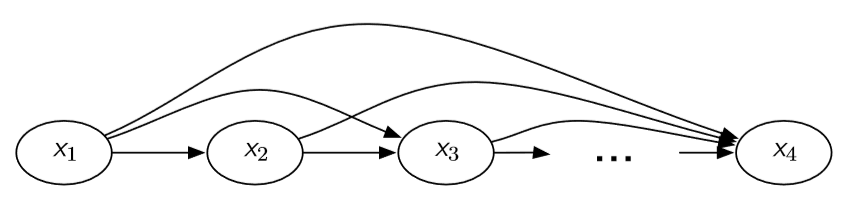
  $$p_{{\mathrm{x}}_1,\dots ,{\mathrm{x}}_n}=p_{{\mathrm{x}}_1}\left(x_1\right)p_{{\mathrm{x}}_2|{\times }_1}\left(x_2|x_1\right)\cdots p_{{\mathrm{x}}_n|x_1,\dots ,x_{n-1}}\left(x_n|x_1,\dots ,x_{n-1}\right)$$
  

• Directed acyclic graphs (DAG)

• Fully-connected DAG

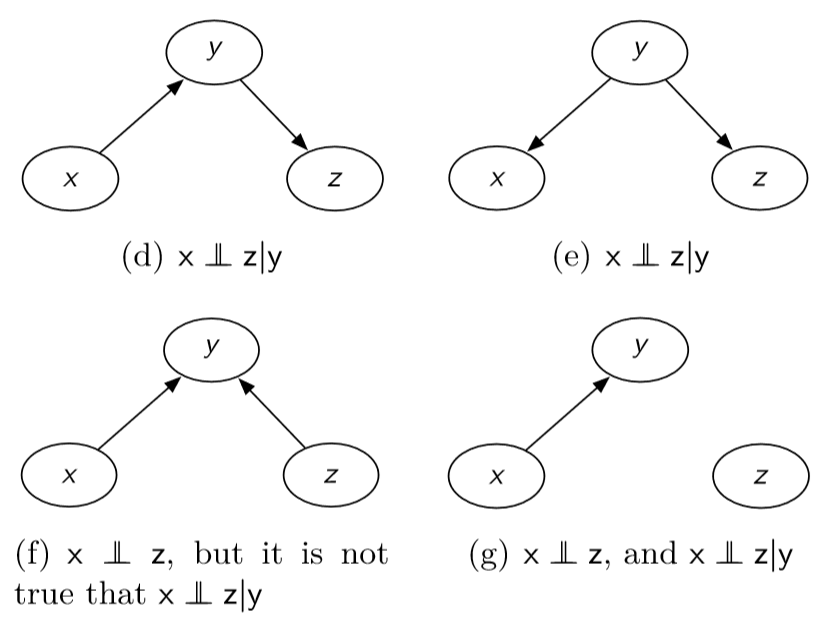
• conditional independence：${\mathbf{x}}_{{\mathcal{A}}_1}\perp {\mathbf{x}}_{{\mathcal{A}}_2}|{\mathbf{x}}_{{\mathcal{A}}_3}$

  

• Bayes ball algorithm

  • primary shade: ${\mathcal{A}}_3$ 中的节点
  • secondary shade: primary shade 的节点，以及 secondary shade 的父节点

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8UKlSiFL-1580777349196)(C:Users1AppDataRoamingTyporatypora-user-images1574319393095.png)]

3. Factor graph

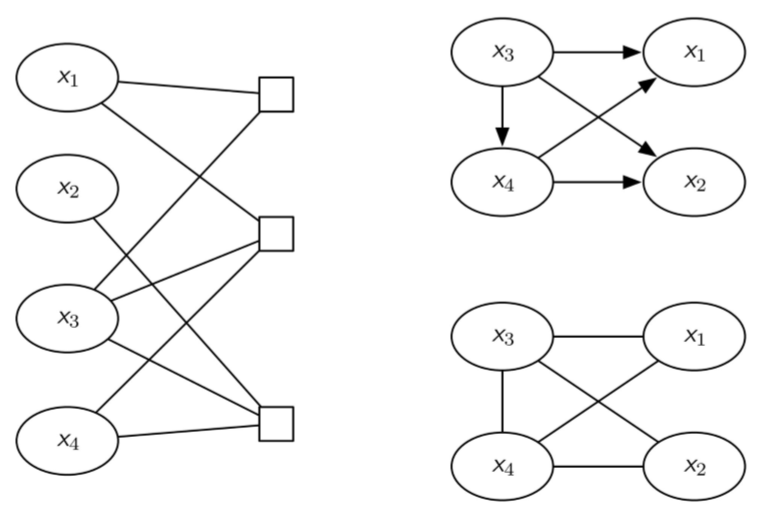
• 有 variable nodes 和 factor nodes，是 bipartitie graph
  $$p_{\mathbf{x}}(\mathbf{x})\propto \prod _j{f}_j\left({\mathbf{x}}_{f_j}\right)$$
  

• 因子图比 directed graph 和 undirected graph 的表示能力更强，比如 $p(x)=\frac{1}{Z}{\varphi }_{12}(x_1,x_2){\varphi }_{13}(x_1,x_3){\varphi }_{23}(x_2,x_3)$

• 因子图可以与 DAG 相互转化(根据 $x_1,...,x_n$ 依次根据 conditional independence 决定父节点)，DAG又可以转化为 undirected graph

4. Measuring goodness of graphical representations

• 给定分布 D 和图 G，他们之间没必要有联系
• $CI(D)$：the set of conditional independencies satisfied by $D$
• $CI(G)$： the set of all conditional independencies implied by $G$
• I-map：$CI(\mathcal{G})\subset CI(D)$
• D-map: ：$CI(\mathcal{G})\supset CI(D)$
• P-map：$CI(\mathcal{G})=CI(D)$
• minimal I-map: Aminimal I-mapisanI-mapwiththepropertythatremovinganysingle edge would cause the graph to no longer be an I-map.
  Remarks: G 中去掉一个边会使该 map 中有更多的 conditional independence，也即 $CI(G)$ 更大，更不易满足 I-map条件。I-map 可以表示分布 D，但是 D-map 不能

其他内容请看：
统计推断(一) Hypothesis Test
统计推断(二) Estimation Problem
统计推断(三) Exponential Family
统计推断(四) Information Geometry
统计推断(五) EM algorithm
统计推断(六) Modeling
统计推断(七) Typical Sequence
统计推断(八) Model Selection
统计推断(九) Graphical models
统计推断(十) Elimination algorithm
统计推断(十一) Sum-product algorithm

最后

以上就是欣慰电灯胆最近收集整理的关于统计推断(九) Graphical models的全部内容，更多相关统计推断(九)内容请搜索靠谱客的其他文章。