simrank

1. simrank的基本思想

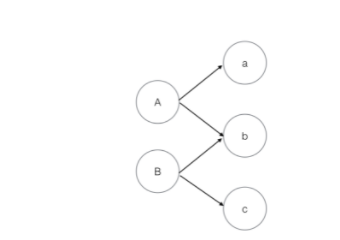
基于图结构的相似度计算方法，如果两个实体相似，那么跟它们相关的实体应该也相似。就如下图，如果a和c相似，那么A和B应该也相似，因为A和a相关，而B和c相关。

基本公式：

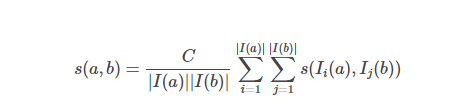
直接使用上面的迭代公式很难展开并行计算，数量稍微大一些（比如上十万）时在单机上跑时间和空间开销非常大。所以给出矩阵形式

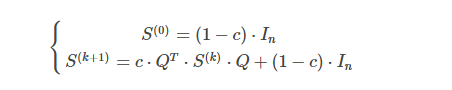
例1.计算图1中节点SimRank相似度，其中c=0.6

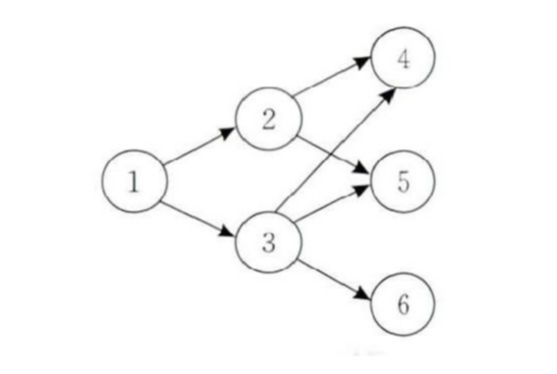
根据定义，每个节点跟自己相似度为1，由于节点1没有入边，因此节点1与任何节点相似度为0
s(2,3)=$\frac{c}{1\ast 1}$(s(1,1))=0.6
s(4,5)=$\frac{c}{2\ast 2}$(s(2,2)+s(2,3)+s(3,2)+s(3,3))=0.48
s(5,6)=$\frac{c}{2\ast 1}$(s(2,3)+s(3,3))=0.48
s(4,6)=$\frac{c}{2\ast 1}$(s(2,3)+s(3,3))=0.48
输入：有向图
输出：全体节点相似集
下面是一张网页链接关系图，表示一所大学的主页上放了A、B两个教授的个人主页的链接，教授B和学生B的个人主页互相链接了对方，等等。下面我们要通过这种链接关系求这5个节点的相似度。

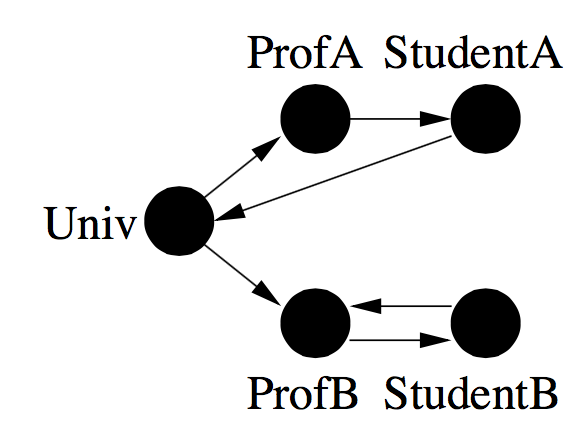
首先用一个文本文件存储上面的有向图

univ    profA   profB
profA   studentA
studentA    univ
profB   studentB
studentB    profB

sim_test.py

#!/usr/bin/env python
# coding=utf-8

import numpy as np
import scipy as sp
from functools import cmp_to_key

nodes = []  # 所有的节点存入数组
nodesnum = 0  # 所有节点的数目
nodes_index = {}  # <节点名，节点在nodes数组中的编号>
damp = 0.8  # 阻尼系数
trans_matrix = np.matrix(0)  # 转移概率矩阵
sim_matrix = np.matrix(0)  # 节点相似度矩阵


def initParam(graphFile):
    '''
    构建nodes、nodes_index、trans_matrix和第0代的sim_matrix.
    输入文件行格式要求：nodetoutneighbortoutneighbort...或 nodetinneighbortinneighbort...
    '''
    global nodes
    global nodes_index
    global trans_matrix
    global sim_matrix
    global damp
    global nodesnum

    link_in = {}
    for line in open(graphFile, "r", 1024):
        arr = line.strip("n").split()   # 去除换行符，以空格为分隔符，['univ', 'profA', 'profB']
        node = arr[0]                    # 存入节点数组
        nodeid = -1
        if node in nodes_index:
            nodeid = nodes_index[node]

        else:
            #print(nodes)
            nodeid = len(nodes)
            #print(nodeid)
            nodes_index[node] = nodeid
            nodes.append(node)
        for ele in arr[1:]:
            outneighbor = ele
            outneighborid = -1
            if outneighbor in nodes_index:
                outneighborid = nodes_index[outneighbor]
            else:
                outneighborid = len(nodes)
               # print(outneighborid)
                nodes_index[outneighbor] = outneighborid
                #print(nodes_index)
                nodes.append(outneighbor)
               # print(nodes)
            inneighbors = []
            if outneighborid in link_in:
                inneighbors = link_in[outneighborid]
            inneighbors.append(nodeid)
            #print(inneighbors)
            link_in[outneighborid] = inneighbors
            #print(link_in)

    nodesnum = len(nodes)
    trans_matrix = np.zeros((nodesnum, nodesnum))
    print(trans_matrix)
    print(link_in)
    for node, inneighbors in link_in.items():
        num = len(inneighbors)
        prob = 1.0 / num
        print(inneighbors)
        print(num)
        print(prob)
        for neighbor in inneighbors:
            print(neighbor)
            print(node)
            trans_matrix[neighbor, node] = prob
    print(trans_matrix)
    sim_matrix = np.identity(nodesnum) * (1 - damp) ## np.identity()生成方阵,相似矩阵
    print(nodesnum)
    print(damp)
    print(sim_matrix)



def iterate():
    '''
    迭代更新相似度矩阵
    '''
    global trans_matrix
    global sim_matrix
    global damp
    global nodesnum

    sim_matrix = damp * np.dot(np.dot(trans_matrix.transpose(),
                                      sim_matrix), trans_matrix) + (1 - damp) * np.identity(nodesnum)
    ## np.dot()矩阵积

def printResult(sim_node_file):
    '''
    打印输出相似度计算结果
    '''
    global sim_matrix
    global link_out
    global link_in
    global nodes
    global nodesnum

    # 打印node之间的相似度
    f_out_user = open(sim_node_file, "w")
    for i in range(nodesnum):
        f_out_user.write(nodes[i] + "t")
        neighbour = []
        for j in range(nodesnum):
            if i != j:
                sim = sim_matrix[i, j]
                if sim == None:
                    sim = 0
                if sim > 0:
                    neighbour.append((j, sim))
        # 按相似度由大到小排序
        ##neighbour = sorted(neighbour, cmp_to_key=lambda x, y: cmp_to_key(x[1], y[1]), reverse=True)
        neighbour.sort(key=cmp_to_key(lambda x,y:x[1]-y[1]),reverse=True)
        for (u, sim) in neighbour:
            f_out_user.write(nodes[u] + ":" + str(sim) + "t")
        f_out_user.write("n")
    f_out_user.close()


def simrank(graphFile, maxIteration):
    global nodes_index
    global trans_matrix
    global sim_matrix

    initParam(graphFile)
    print
    "nodes:"
    print
    nodes_index
    print
    "trans ratio:"
    print
    trans_matrix
    for i in range(maxIteration):
        print
        "iteration %d:" % (i + 1)
        iterate()
        print
        sim_matrix
if __name__ == '__main__':
    graphFile ="link_graph.txt"
    ##graphFile = "graph_bipartite.txt"
    sim_node_file = "nodesim_naive.txt"
    maxIteration = 10
    simrank(graphFile, maxIteration)
    printResult(sim_node_file)

输出结果

univ	profB:0.10803511296000001	studentB:0.022030581760000004	
profA	profB:0.36478881792	studentB:0.08159625216000001	
profB	profA:0.36478881792	univ:0.10803511296000001	studentB:0.0642220032	studentA:0.030222581760000002	
studentA	studentB:0.28216737791999996	profB:0.030222581760000002	
studentB	studentA:0.28216737791999996	profA:0.08159625216000001	profB:0.0642220032	univ:0.022030581760000004	

例2.将user，item划分成二部图关系，每个user和item都是独立的点，user在不同item上产生用户行为，则是一条边，对于下面的例子而言，左边的搜索词是user，右边的网址就是item

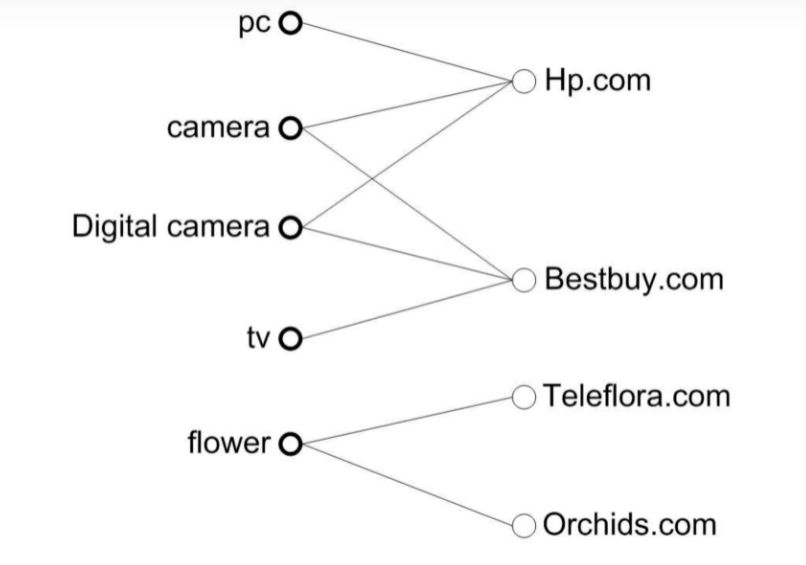
基本思想：汇聚到相同的item点的user，相互之间具有相似性
计算s(q1,q2)的思路：直接统计2个搜索词的网址集合之间交集的大小。即|E(q1)$\bigcap$E(q2)
公式化表达成：

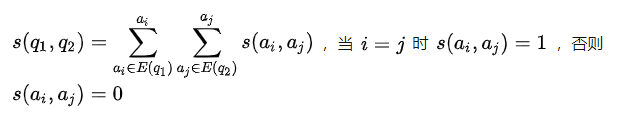
同理计算S(a1,a2)的思路类似：

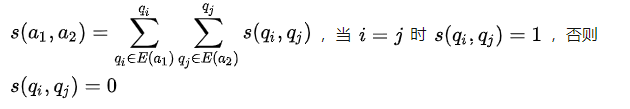
如果搜索词是一个百搭的搜索词，对每个网站都有点击的行为，那么这个搜索词与绝大多数的搜索词类似，这明显是有问题的，为了扼制这类百搭的搜索词，可以设计搜索词的近邻个数作为惩罚项：
$$\frac{c}{|E(q1)|\ast |E(q2)|}$$
计算S(q1,q2)和S(a1,a2)算法可以修改如下：


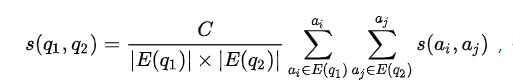
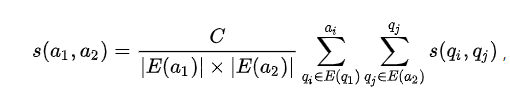
输入文件simple2.txt

pc,hp.com
camera,hp.com
camera,bestbuy.com
digital camera,hp.com
digital camera,bestbuy.com
tv,bestbuy.com
flower,teleflora.com
flower,orchids.com

代码实现

import numpy
from numpy import matrix

with open("simple2.txt", "r") as log_fp:
    logs = [log.strip() for log in log_fp.readlines()]  # 去除换行符，变成列表形式

logs_tuple = [tuple(log.split(",")) for log in logs]  # 以逗号分割

## queries = list(set([log[0] for log in logs_tuple]))
queries = list(set([log[0] for log in logs_tuple]))   # 搜索词列表['digital camera', 'pc', 'tv', 'flower', 'camera']

ads = list(set([log[1] for log in logs_tuple]))  # ['teleflora.com', 'bestbuy.com', 'orchids.com', 'hp.com']

# Graph means the relations number
graph = numpy.matrix(numpy.zeros([len(queries), len(ads)]))  # 初始化矩阵，5行4列矩阵,存放搜索词邻居节点数
for log in logs_tuple:
    query = log[0]
    ad = log[1]
    q_i = queries.index(query)
    a_j = ads.index(ad)
    graph[q_i, a_j] += 1
query_sim = matrix(numpy.identity(len(queries)))  # 初始化搜索词相似性矩阵,对角线为1
ad_sim = matrix(numpy.identity(len(ads)))   # 初始化网址相似性矩阵，对角线为1


def get_ads_num(query):
    q_i = queries.index(query)
    return graph[q_i]


def get_queries_num(ad):
    a_j = ads.index(ad)
    return graph.transpose()[a_j]

# 搜索词的相连网址列表
def get_ads(query):
    series = get_ads_num(query).tolist()[0]  # [0.0, 1.0, 0.0, 1.0]
    return [ads[x] for x in range(len(series)) if series[x] > 0]  # ['hp.com', 'bestbuy.com']


def get_queries(ad):
    series = get_queries_num(ad).tolist()[0]
    return [queries[x] for x in range(len(series)) if series[x] > 0]


def query_simrank(q1, q2, C):
    """
    in this, graph[q_i] -> connected ads
    """
    """
    print "q1.ads"
    print get_ads_num(q1).tolist()
    print "q2.ads"
    print get_ads_num(q2).tolist()
    """
    if q1 == q2: return 1
    prefix = C / (get_ads_num(q1).sum() * get_ads_num(q2).sum())  # 计算惩罚项
    postfix = 0
    for ad_i in get_ads(q1):
        for ad_j in get_ads(q2):
            i = ads.index(ad_i)
            j = ads.index(ad_j)
            postfix += ad_sim[i, j]   # 相连邻居节点相似性
    return prefix * postfix


def ad_simrank(a1, a2, C):
    """
    in this, graph need to be transposed to make ad to be the index
    """
    """
    print "a1.queries"
    print get_queries_num(a1)
    print "a2.queries"
    print get_queries_num(a2)
    """
    if a1 == a2: return 1
    prefix = C / (get_queries_num(a1).sum() * get_queries_num(a2).sum())
    postfix = 0
    for query_i in get_queries(a1):
        for query_j in get_queries(a2):
            i = queries.index(query_i)
            j = queries.index(query_j)
            postfix += query_sim[i, j]
    return prefix * postfix


def simrank(C=0.8, times=2):
    global query_sim, ad_sim
## 迭代相似矩阵
    for run in range(times):
        # queries simrank
        new_query_sim = matrix(numpy.identity(len(queries)))
        print(new_query_sim)
        for qi in queries:
            for qj in queries:
                i = queries.index(qi)
                j = queries.index(qj)
                new_query_sim[i, j] = query_simrank(qi, qj, C)
        print(new_query_sim)
        # ads simrank
        new_ad_sim = matrix(numpy.identity(len(ads)))
        for ai in ads:
            for aj in ads:
                i = ads.index(ai)
                j = ads.index(aj)
                new_ad_sim[i, j] = ad_simrank(ai, aj, C)

        query_sim = new_query_sim
        ad_sim = new_ad_sim


if __name__ == '__main__':
    print(queries)
    print(ads)
    simrank()
    print(query_sim)
    print(ad_sim)

输出结果：

['flower', 'tv', 'digital camera', 'pc', 'camera']
['bestbuy.com', 'orchids.com', 'hp.com', 'teleflora.com']
[[1.         0.         0.         0.         0.        ]
 [0.         1.         0.00144144 0.         0.00213333]
 [0.         0.00144144 1.         0.00216216 0.00172973]
 [0.         0.         0.00216216 1.         0.0032    ]
 [0.         0.00213333 0.00172973 0.0032     1.        ]]
[[1.00000000e+00 0.00000000e+00 9.87654321e-04 0.00000000e+00]
 [0.00000000e+00 1.00000000e+00 0.00000000e+00 3.33333333e-03]
 [9.87654321e-04 0.00000000e+00 1.00000000e+00 0.00000000e+00]
 [0.00000000e+00 3.33333333e-03 0.00000000e+00 1.00000000e+00]

从以上结果可以看出，s(camera,digital camera)小于s(pc,camera),这是不合理的
从两个方面去改进:
1.新增一个补偿项，当两者的交集越多，得到的补偿更多

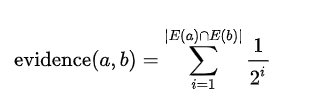
补偿后的修正相似性得分：

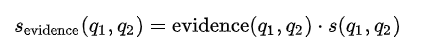
2.每条边都应该有weight属性
3.simrank算法往往面向的是海量的用户数据，所以可以考虑在mapreduce,spark框架上面，实现算法迭代过程的矩阵计算，并行化

最后

以上就是精明超短裙为你收集整理的初识simranksimrank的全部内容，希望文章能够帮你解决初识simranksimrank所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。