目录
前言:
正文:
1. 多臂赌博机
2. ε-greedy策略
3. 玻尔兹曼策略
4. UCB策略
5. 三种策略的多臂赌博机实现
后记:
前言:
这系列笔记是基于郭宪编著的《深入浅出强化学习》而写作的,由于笔者是刚开始学习这方面的知识,不足之处在所难免,希望有问题的地方可以指出。
在这个笔记中,我把大多数代码都加了注释,我的一些想法和注解用蓝色字体标记了出来,重点和需要关注的地方用红色字体标记了出来,这次基本都是我自己总结了,就不标蓝了。
在这一篇文章中,我们主要介绍ε-greedy策略,玻尔兹曼策略,UCB策略在多臂赌博机中的实现。
正文:
1. 多臂赌博机
什么是多臂赌博机?就是一个有k个臂的机器,摇动其中一个臂后,它会爆出数量不等的金币,而爆出金币的数量是服从一定的概率分布的,而且这个概率分布也随不同的臂的变化而变化,也就是说有时候爆出的钱多,有时候钱少,短短几次测试是不能确定哪个臂是最好的。
2. ε-greedy策略
公式就不放上来了(其实是不会敲latex,也不想用其他人的图),这个方法以我来描述就是摇动当前爆金币最多的赌博机概率最高(概率=1-ε),然后随机选动作的概率较低(概率=ε)。
但是这个方法有2个问题,1、衡量变量的角度说,总回报其实不如平均回报合适。2、当前平均回报最好的臂,不一定是最好的那个臂,我们还得保留一定的概率去摇动其他的臂来发现更好的臂。
3. 玻尔兹曼策略
也没有公式,这一个策略与ε-greedy策略不同的是,这个策略根据对应的值函数对摇哪个臂的概率进行了软处理,也就是说平均爆金币多的机器更有可能选中。这个策略中引入了一个参数(temperature)此参数越小,这个策略就越接近贪婪策略(更可能选平均爆金币最多的),参数越大,就越接近均匀策略(更可能随便选)
4. UCB策略
还是没有公式,UCB的全称是Upper Confidence Bound(置信上界),这个策略的特点是当对一个臂的了解不够时(可以认为它的方差很大,现在只是运气不好),它会被选中。
5. 三种策略的多臂赌博机实现
主要需要注意的地方都写在注释里面了,使用了numpy和matploblib两个库,如果运行不了的话请注意。
样例:
"这里主要是进行一个多臂赌博机的强化学习练习,作为一个初始作品,希望能有一个好的开头"
import numpy as np
import matplotlib.pyplot as plt
class KB_Game:
def __init__(self, *args, **kwargs):
self.q = np.array([0.0, 0.0, 0.0]) # 每个臂的平均汇报回报
self.action_counts = np.array([0, 0, 0]) # 摇动每个臂的次数
self.current_cumulative_rewards = 0.0 # 累计回报总和
self.actions = [1, 2, 3] # 动作空间,1,2,3表示三个不同的摇臂
self.counts = 0 # 玩家玩游戏的次数
self.counts_history = [] # 玩家玩游戏的次数记录
self.current_cumulative_rewards_history = [] # 累积回报的记录
self.a = 1 # 玩家当前动作,初始值可以为动作空间中任意一个动作,这里是去摇动第一个臂
self.reward = 0 # 当前回报,初始值为0
def step(self, a):
r = 0
if a == 1: # 摇动摇臂1
r = np.random.normal(1, 1) # 回报符合均值为1,标准差为1的正态分布
if a == 2:
r = np.random.normal(2, 1) # 回报符合均值为2,标准差为1的正态分布
if a == 3:
r = np.random.normal(1.5, 1) # 回报符合均值为1.5,标准差为1的正态分布
return r
def choose_action(self, policy, **kwargs): # kwargs是一个dict,python自带的,这里传递的是策略对应的超参数,
action = 0
if policy == 'e_greedy': # e_greedy方法
if np.random.random() < kwargs['epsilon']:
# np.random.random()是0~1的随机数,kwargs['epsilon']对应的是epsilon(那个希腊符号)
action = np.random.randint(1, 4) # random.randint(1, 4)是返回1~4-1的一个随机整型
else:
action = np.argmax(self.q) + 1 # 返回平均回报最大的那个
if policy == 'ucb': # ucb策略可以看https://blog.csdn.net/songyunli1111/article/details/83384738
c_ratio = kwargs['c_ratio']
if 0 in self.action_counts: # 在有哪一个没试过一次的情况下
action = np.where(self.action_counts == 0)[0][0] + 1 # 就去试一下那个臂
else:
value = self.q + c_ratio*np.sqrt(np.log(self.counts)/self.action_counts) # 算法实现
action = np.argmax(value) + 1 # 感觉这个怪怪的,直接找value最大的?
if policy == 'boltzmann': # 玻尔兹曼方法
tau = kwargs['temperature']
p = np.exp(self.q/tau)/(np.sum(np.exp(self.q/tau))) # p是抽取每个臂的概率,一个不知道几维的数组
action = np.random.choice([1, 2, 3], p=p.ravel())
# ravel函数是把p拉成一维数组,这里np.random.choice的前一个参数是选取范围,后一个是各个的概率
return action
# 这里play_total是它的训练的总次数,policy是训练方法(e_greedy之类),**kwargs是它的超参数(temperature之类)
def train(self, play_total, policy, **kwargs):
# 下面这几个reward我是不太明白,估计是在看到结果后,调出reward就能看到平均回报的变化,在这个程序里应该是没有用上的
reward_1 = []
reward_2 = []
reward_3 = []
for i in range(play_total): # 总共玩多少次
action = 0
if policy == 'e_greedy': # 选择方法
action = self.choose_action(policy, epsilon=kwargs['epsilon'])
if policy == 'ucb':
action = self.choose_action(policy, c_ratio=kwargs['c_ratio'])
if policy == 'boltzmann':
action = self.choose_action(policy, temperature=kwargs['temperature'])
self.a = action
# print(self.a) 打印的是整型数字
# 与环境交互一次
self.reward = self.step(self.a) # 说实话我感觉应该写成reward,书上啥都有,这里都写成了r,那就改过来吧
self.counts += 1
# 更新值函数
self.q[self.a-1] = (self.q[self.a-1]*self.action_counts[self.a-1]+self.reward)/(self.action_counts[self.a-1]+1)
# 更新平均回报
self.action_counts[self.a-1] += 1
reward_1.append([self.q[0]])
reward_2.append([self.q[1]])
reward_3.append([self.q[2]])
# 下面是对累计回报和历史累计回报进行更新
self.current_cumulative_rewards += self.reward
self.current_cumulative_rewards_history.append(self.current_cumulative_rewards)
self.counts_history.append(i)
def reset(self): # 只是把init函数里的actions删掉了而已,这个是用来重置KB_Game中的成员变量的函数
self.q = np.array([0.0, 0.0, 0.0])
self.action_counts = np.array([0, 0, 0])
self.current_cumulative_rewards = 0.0
self.counts = 0
self.counts_history = []
self.current_cumulative_rewards_history = [] # self.cumulative_rewards_history = []书上是这玩意
self.a = 1
self.reward = 0
def plot(self, colors, policy): # 绘图函数
plt.figure(1)
plt.plot(self.counts_history, self.current_cumulative_rewards_history, colors, label=policy)
plt.legend()
plt.xlabel('n', fontsize=18)
plt.ylabel('total rewards', fontsize=18)
if __name__ == '__main__':
np.random.seed(0) # 要改成时间不同就不同的话就把0改掉就行了
k_gamble = KB_Game()
total = 2000 # 总共游玩的次数
# 下面是各个方法的使用了,就不一个个强调了
k_gamble.train(play_total=total, policy='e_greedy', epsilon=0.05)
k_gamble.plot(colors='r', policy='e_greedy') # 这书上的plot函数本来就没有style传进去,看来得改改,把style删了哈哈哈
k_gamble.reset()
k_gamble.train(play_total=total, policy='boltzmann', temperature=1)
k_gamble.plot(colors='b', policy='boltzmann')
k_gamble.reset()
k_gamble.train(play_total=total, policy='ucb', c_ratio=0.5)
k_gamble.plot(colors='g', policy='ucb')
plt.show()
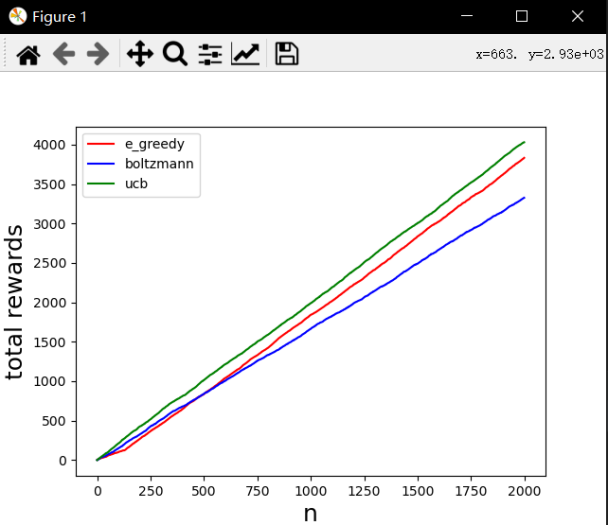
图为跑出来的结果,看来boltzmann策略的参数得设置好,不然去赌博的时候怎么亏钱都不知道了(我才不会赌博呢)
后记:
第一次做强化学习的笔记,做完之后感到自己已经把python的知识忘光啦~,那应该怎么办呢?当然是重新拾起来啦!怎么拾起来呢?那就哪里不会搜哪里吧!配置环境就是这样搞定的,只要我访问的网页够多,就绝对有解决方案,如果找不到的话,那就一定是找的不够多!不过我还是挺乐在其中哈,不觉得这寻找解决方案的过程就像侦探追凶吗?当你关掉了几十个网页,长舒一口气时,感觉就像破案了一样快乐。
最后
以上就是玩命世界最近收集整理的关于强化学习学习笔记(一) 几种策略在多臂赌博机的实现前言:正文:后记:的全部内容,更多相关强化学习学习笔记(一)内容请搜索靠谱客的其他文章。








发表评论 取消回复