概述
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档
FPGA信号处理系列文章——定点数据截位处理
- 前言
- 截位方法
- Truncation
- Non-symmetric Rounding to Positive
- Non-symmetric Rounding to Negative
- Symmetric Rounding to Highest Magnitude
- Symmetric Rounding to Zero
- Convergent Rounding to even
- Convergent Rounding to odd
- matlab频谱分析
- 总结
前言
在我们FPGA的设计中，截位和扩位都是很常见的操作。
有截高位、低位和扩高位、扩低位之分。
1、截高位表示截取掉信号过多的符号位，在我们确认该数据确实不需要这么宽的位宽时，直接可以把高位符号位去掉，这个时候该信号的幅值不会发生任何变化
2、扩高位一般是两个模块端口进行匹配，扩高位即扩符号位，这个时候该信号的幅值不会发生任何变化
3、扩低位一般是在低位上补0，相当于在原来的值乘以2的几次方，对于信号来说没有任何损失，只是幅度变大了而已。
4、截低位 ，这个就是我们这篇文章需要讨论的，因为截低位对于信号来说是有变化和损失的，那么我们来分析一下一些主要的截位方法
截位方法
由于输入数据和滤波器系数都是已经定点化的数据，xilinx fir ip核给我们提供了几种截位的方法
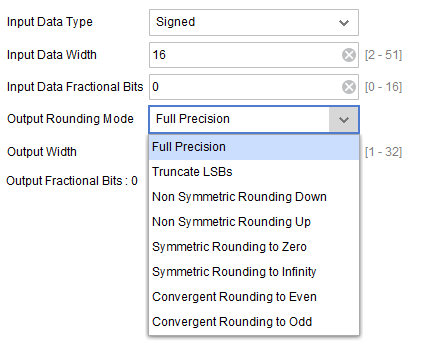
可以认为这些方法就是我们平时会用到的一些截位方法了，我们正好借用一下来进行分析
Truncation
直接舍弃数据的低位，相当于matlab 的floor函数
matlab:
'假设我们要截低5位，a是待截数据
floor(32/32) = 1 floor(33/32) = 1 floor(48/32) = 1
floor(63/32) = 1 floor(64/32) = 2
floor(-32/32) = -1 floor(-33/32) = -2
floor(-48/32) = 2 floor(-63/32) = -2 floor(-64/32) = -2
b = floor(a/2^5);
verilog:
32: 10'b00_0010_0000 33: 10'b00_0010_0001 48: 10'b00_0011_0000
63: 10'b00_0011_1111 64: 10'b00_0100_0000
-32: 10'b11_1110_0000 -33: 10'b11_1101_1111 -48: 10'b11_1101_0000
-63: 10'b11_1100_0001 -64: 10'b11_1100_0001
b = a[9:5]
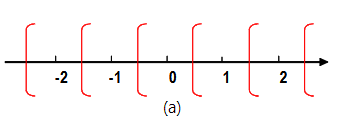
Non-symmetric Rounding to Positive
先把数据加上0.5，然后舍弃数据的低位。相当于matlab的floor(x+0.5)
matlab:
'假设我们要截低5位，a是待截数据
floor((32+16)/32) = 1 floor((33+16)/32) = 1 floor((48+16)/32) = 2
floor((63+16)/32) = 2 floor((64+16)/32) = 2
floor((-32+16)/32) = -1 floor((-33+16)/32) = -1 floor((-48+16)/32) = -1
floor((-63+16)/32) = -2 floor((-64+16)/32) = -2
b = floor((a+2^4)/2^5);
verilog:
32: 10'b00_0010_0000 33: 10'b00_0010_0001 48: 10'b00_0011_0000
63: 10'b00_0011_1111 64: 10'b00_0100_0000
-32: 10'b11_1110_0000 -33: 10'b11_1101_1111 -48: 10'b11_1101_0000
-63: 10'b11_1100_0001 -64: 10'b11_1100_0001
b1 = a + 10'b00_0001_0000
b = a[9:5]
or
b = a[9:5]+a[4]
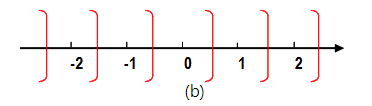
Non-symmetric Rounding to Negative
先把数据加上0.4999999…，然后舍弃数据的低位.。相当于matlab的ceil(x-0.5)
'假设我们要截低5位，a是待截数据
floor((32+16-1)/32) = 1 floor((33+16-1)/32) = 1 floor((48+16-1)/32) = 1
floor((63+16-1)/32) = 2 floor((64+16-1)/32) = 2
floor((-32+16-1)/32) = -1 floor((-33+16-1)/32) = -1 floor((-48+16-1)/32) = -2
floor((-63+16-1)/32) = -2 floor((-64+16-1)/32) = -2
b = ceil((a-2^4)/2^5);
or b = floor((a+2^4-1)/2^5);
verilog:
32: 10'b00_0010_0000 33: 10'b00_0010_0001 48: 10'b00_0011_0000
63: 10'b00_0011_1111 64: 10'b00_0100_0000
-32: 10'b11_1110_0000 -33: 10'b11_1101_1111 -48: 10'b11_1101_0000
-63: 10'b11_1100_0001 -64: 10'b11_1100_0001
b1 = a + 10'b00_0000_1111
b = a[9:5]
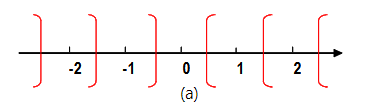
Symmetric Rounding to Highest Magnitude
相当于matlab 的round函数
'假设我们要截低5位，a是待截数据
round(32/32) = 1 round(33/32) = 1 round(48/32) = 2
round(63/32) = 2 round(64/32) = 2
round(-32/32) = -1 round(-33/32) = -1
round(-48/32) = -2 round(-63/32) = -2 round(-64/32) = -2
b = round(a/2^5);
verilog:
32: 10'b00_0010_0000 33: 10'b00_0010_0001 48: 10'b00_0011_0000
63: 10'b00_0011_1111 64: 10'b00_0100_0000
-32: 10'b11_1110_0000 -33: 10'b11_1101_1111 -48: 10'b11_1101_0000
-63: 10'b11_1100_0001 -64: 10'b11_1100_0001
if(a >= 0)
b1 = a + 10'b00_0001_0000
b = a[9:5]
else if(a < 0)
b1 = a + 10'b00_0000_1111
b = a[9:5]
Symmetric Rounding to Zero
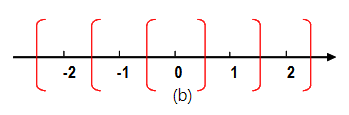
这种截位方式不会发生溢出
'假设我们要截低5位，a是待截数据
round(32/32) = 1 round(33/32) = 1 floor(48/32) = 1
round(63/32) = 2 round(64/32) = 2
round(-32/32) = -1 round(-33/32) = -1
ceil(-48/32) = -1 round(-63/32) = -2 round(-64/32) = -2
if (a >= 0 & mod(a,32) == 16 )
b = floor(a/2^5);
elseif (a < 0 & mod(a,32) == 16)
b = ceil(a/2^5);
else
b = round(a/2^5);
end
这里verilog就不再描述了,看起来有点复杂，暂时没想到简单的写法，想到了再补充
Convergent Rounding to even
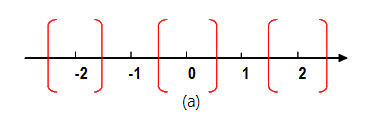
Convergent Rounding to odd
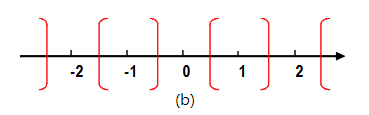
收敛舍入选择中点的舍入方向为奇数或偶数，而不是正数或负数。 这可能是有利的，因为中点舍入方向决策的平衡基于奇数或偶数出现的概率，即使在输入信号的均值远离零时，在大多数情况下这通常是相等的。 该功能是通过添加舍入常数来实现的，就像在其他模式中一样，然后检查 LSB 上的特定模式以检测中点并强制 LSB 为零（舍入到偶数）或 1（舍入到奇数） ) 当出现中点时
这里matlab和verilog就不再描述了,看起来更复杂，暂时没想到简单的写法，想到了再补充。这两种情况应该一般用的不多。
matlab频谱分析
这里把前面5种截位方法用matlab进行分析，我们以一个点频作为例子
close all;clear all; clc;
fi = 1;
fs = 100;
n = [-500000:500000];
a = 2048*exp(j*2*pi*fi/fs*n)+256*randn(1,length(n));
b = floor(a/2^5);
c = floor((a+2^4)/2^5);
d = ceil((a-2^4)/2^5);
e = round(a/2^5);
a1 = real(a);
for i = 1:length(a1)
if (a1(i) >= 0 & mod(a1(i),32) == 16 )
f1(i) = floor(a1(i)/2^5);
elseif (a1(i) < 0 & mod(a1(i),32) == 16)
f1(i) = ceil(a1(i)/2^5);
else
f1(i) = round(a1(i)/2^5);
end
end
a1 = imag(a);
for i = 1:length(a1)
if (a1(i) >= 0 & mod(a1(i),32) == 16 )
f2(i) = floor(a1(i)/2^5);
elseif (a1(i) < 0 & mod(a1(i),32) == 16)
f2(i) = ceil(a1(i)/2^5);
else
f2(i) = round(a1(i)/2^5);
end
end
f = f1+f2*1j;
bfft = 20*log10(abs(fftshift(fft(b))));
cfft = 20*log10(abs(fftshift(fft(c))));
dfft = 20*log10(abs(fftshift(fft(d))));
efft = 20*log10(abs(fftshift(fft(e))));
ffft = 20*log10(abs(fftshift(fft(f))));
figure(1)
subplot(5,1,1)
plot(n,bfft);grid on;
subplot(5,1,2)
plot(n,cfft);grid on;
subplot(5,1,3)
plot(n,dfft);grid on;
subplot(5,1,4)
plot(n,efft);grid on;
subplot(5,1,5)
plot(n,ffft);grid on;
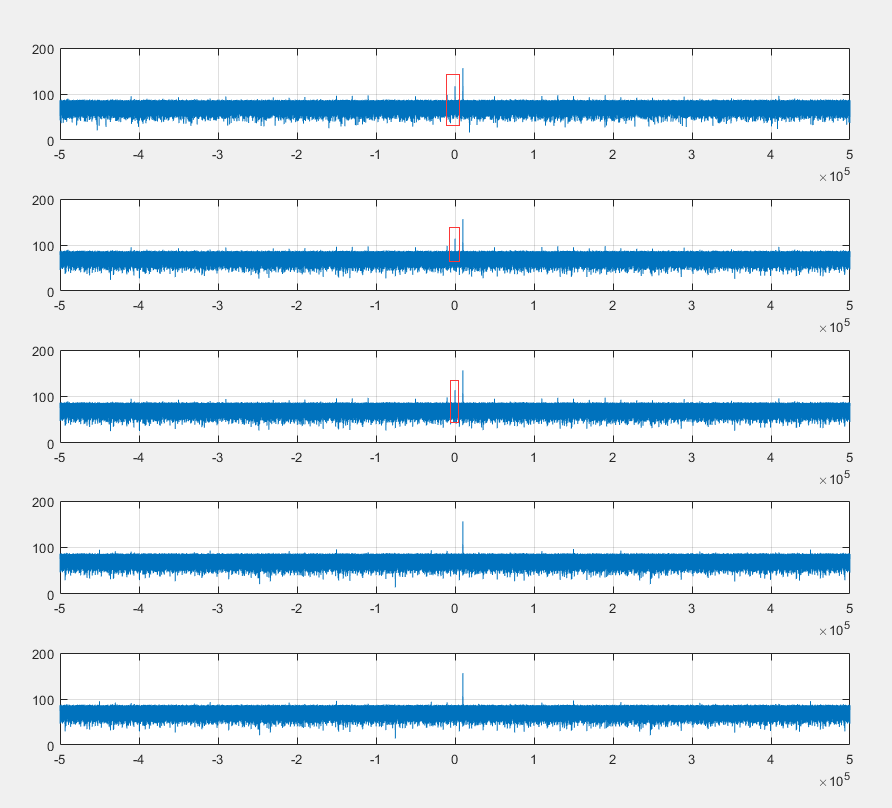
可以看出 非对称截位都会引起一个直流量。
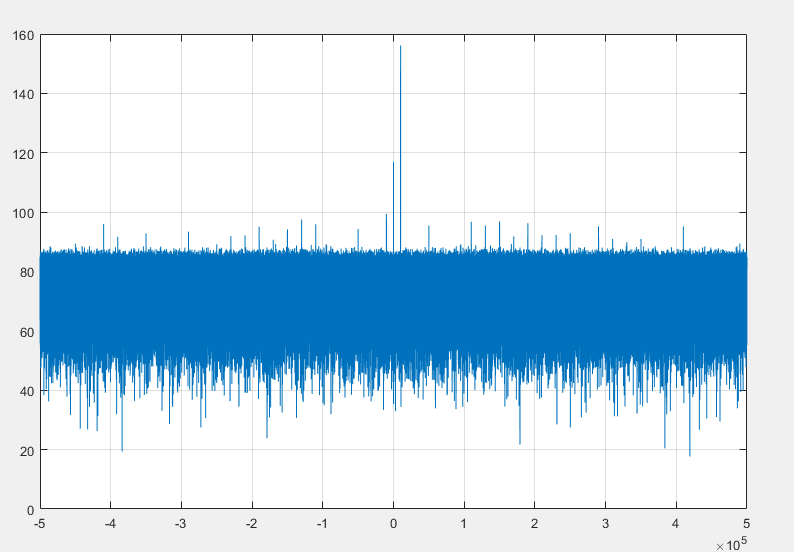
这个直流量不会随着主信号的幅度变化，其幅度始终保持不变。
这种直流是我们需要避免的。因此我们截位需要用对称截位。
总结
我们在进行信号处理需要使用截位的时候要用对称截位。
如果对于只是进行运算类的截位，例如功率统计这种，则不需要，简单的直接截位即可。这点是我们在设计中需要注意的
最后
以上就是精明老鼠为你收集整理的FPGA信号处理系列文章——定点数据截位处理前言截位方法TruncationNon-symmetric Rounding to PositiveNon-symmetric Rounding to NegativeSymmetric Rounding to Highest MagnitudeSymmetric Rounding to ZeroConvergent Rounding to evenConvergent Rounding to oddmatlab频谱分析总结的全部内容，希望文章能够帮你解决FPGA信号处理系列文章——定点数据截位处理前言截位方法TruncationNon-symmetric Rounding to PositiveNon-symmetric Rounding to NegativeSymmetric Rounding to Highest MagnitudeSymmetric Rounding to ZeroConvergent Rounding to evenConvergent Rounding to oddmatlab频谱分析总结所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复