BipedalWalkerHardcore_v3游戏下基于TD3的强化学习算法
本项目依托于gym库下BipedalWalkerHardcore_v3(双足机器人硬核版)游戏环境,通过TD3算法实现通关。
1. 项目准备
本项目利用AIStudio实现,运行环境如下表。其中gym库建议一致,否则可能会出现找不到BipedalWalkerHardcore_v3的情况。
| 名称 | 版本 | 说明 |
|---|---|---|
| AIStudio | 经典版 | 代码实现的基础平台与环境 |
| PaddlePaddle | 2.1.2 | 新建项目时选择 |
| python | 3.7 | 默认选择 |
| gym | 0.25.2 | 强化学习交互环境库 |
| visualdl | 2.2.0 | 记录训练数据 |
2. 游戏环境介绍
BipedalWalkerHardcore_v3是一个四关节双足机器人环境,其中有梯子、树桩、陷阱等障碍物,在1600个时间步中得到300分即可通关这一环境。在这个环境中,机器人需要与环境不断交互,并最终习得跑步、避障、跳跃、上下台阶等技能,传统的强化学习算法难以胜任这一任务,本项目采用TD3算法最终获得较好的收敛效果。如下表是一些交互参数的介绍。
| 变量名 | 说明 |
|---|---|
| action | 四个关节点机速度值,范围在[-1,1] |
| state | 由角速度、水平速度、垂直速度、关节位置、腿与地面的接触及10个激光雷达测量值组成的24维向量 |
| reward | 每次跌倒获得-100分,驱动关节转动得到少量的负分,前进获得正分,总计到300分即可获胜 |
| done | 摔倒、获胜、达到最大时间步均会结束当前轮 |
3. TD3网络介绍
TD3(Twin Delayed Deep Deterministic policy gradient algorithm,双延迟深度确定性策略梯度算法)适合于具有高维连续动作空间的任务。
其中的Deep Deterministic policy gradient,也就是DDPG算法,因此TD3其实就是DDPG的一个优化版本。
具体的优化主要是以下三个方面,理解了这些优化基本上也就可以理解TD3算法了。
3.1 双网络
让我们首先看一下DDPG的网络结构图如下:
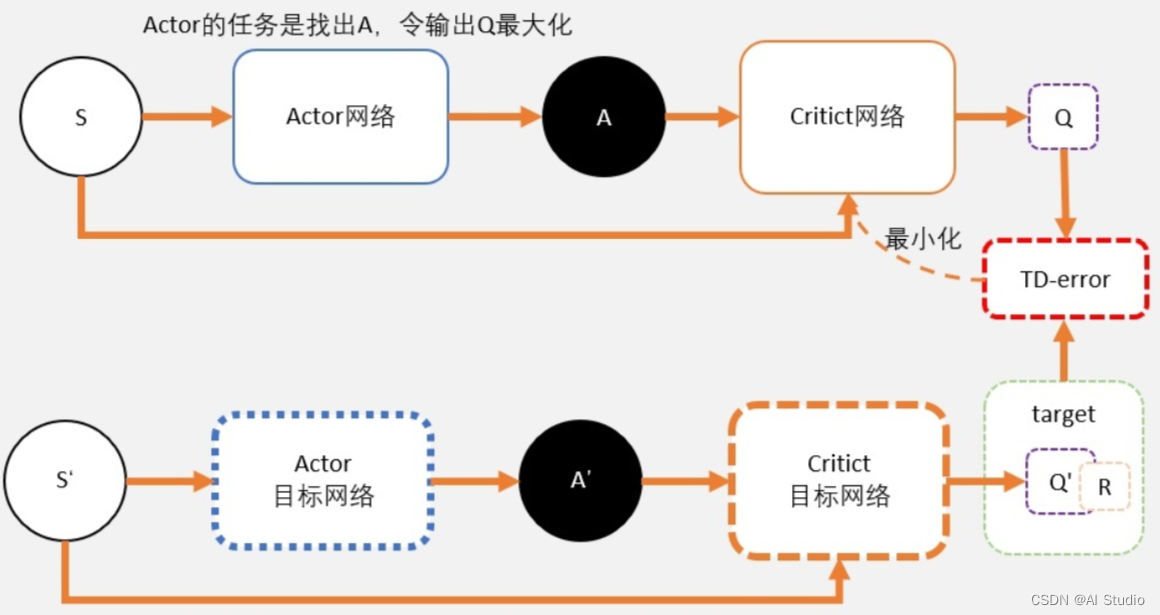
其中Actor用于将不同的state映射为对应的action,即决策在不同的state下应该采取什么洋的动作。而Crite就是用来评判采取不同的action最终可以获得多少分,从而使得机器人可以获得更高的分数。
众所周知,在DQN算法中Q值会被过高估计,而DDPG起源于DQN不可避免也会存在这样的情况。为解决这一问题,提出了double DQN算法。在TD3中,也仿照这一思路,采用了两套网络估算Q值,选择其中较小的一个作为更新的目标,如下图:
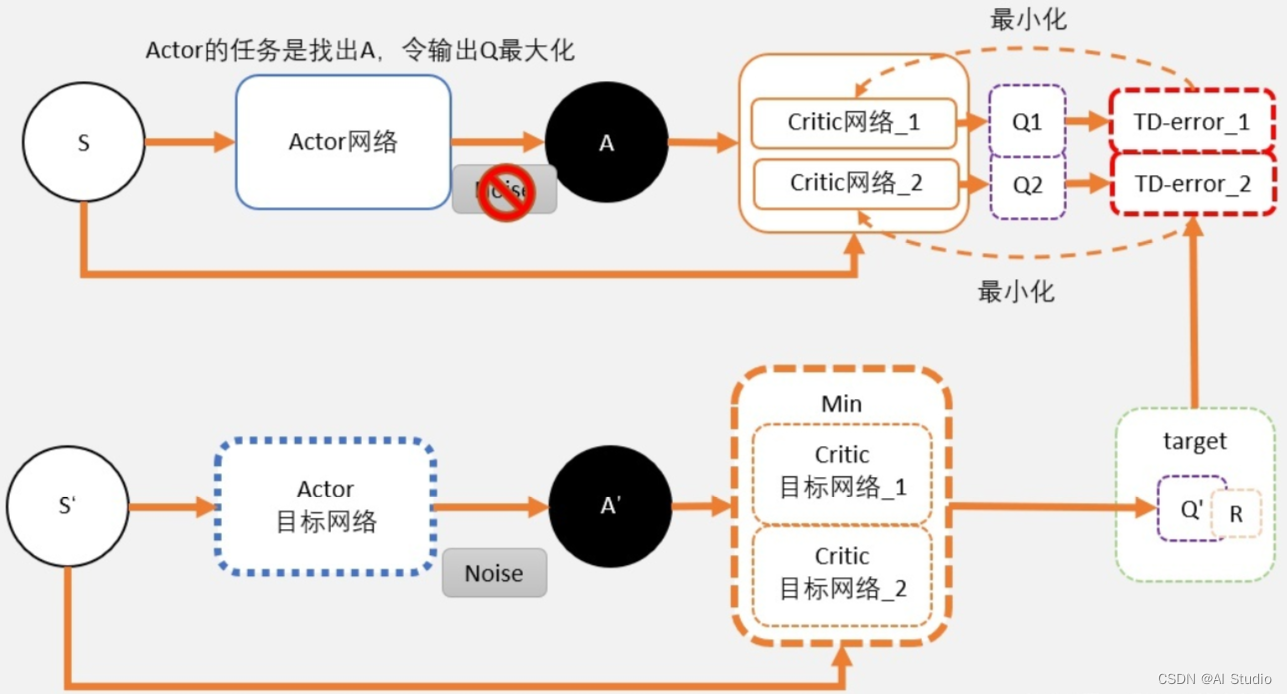
可见,我们采用两个Critic网络评判A值,选择其中较小的一个,从而避免了Critic评估值过高。
而对于Actor来说,由于其任务是不断梯度上升寻找最大Q,随着网络不断更新,最终两个网络也会变得越来越像,所以用Q1还是Q2对Actor并没有太大影响。
3.2 延迟更新
在学习的过程中,Q值是不断变化的,因此梯度上升寻找最大Q对于Actor来说具有很大的挑战,很容易陷在次高点。因此把Critic的更新频率调的比Actor高一点,多学习几次再来指导Actor网络,从而让Actor可以更好的寻找最高点。
3.3 噪声平滑
在TD3中,价值函数的更新目标每次都会在action上加一个微小扰动。不同于DDPG中的滑动平均值更新,微小的扰动可以让action在一定小范围内随机,从而可以更充分的理解游戏空间,使得网络更健壮。
4. 效果演示
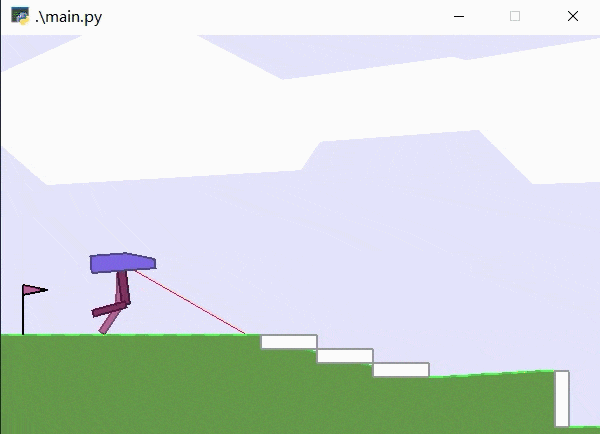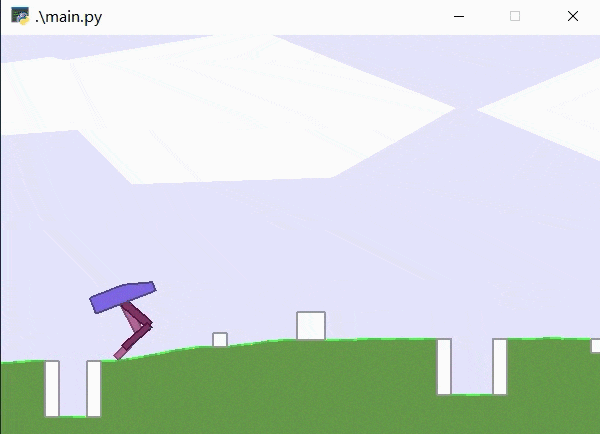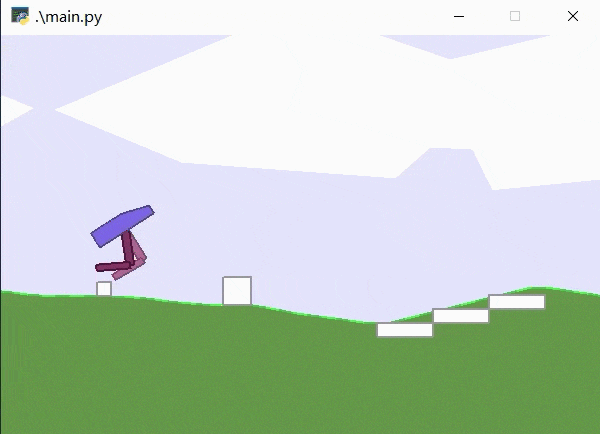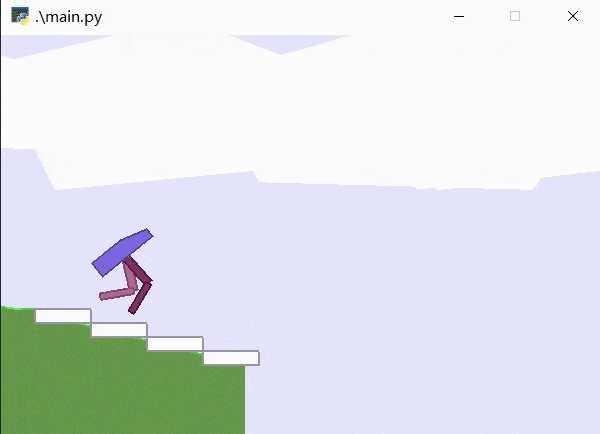
其加载模型为7500轮训练结果,可见已经可以较好地完成该游戏任务。
5. 网络搭建
首先导入相关库文件。
import copy
import numpy as np
import paddle
import paddle.nn as nn
import paddle.nn.functional as F
5.1 Actor网络
class Actor(nn.Layer):
def __init__(self, state_dim, action_dim, net_width, maxaction):
super(Actor, self).__init__()
self.l1 = nn.Linear(state_dim, net_width)
self.l2 = nn.Linear(net_width, net_width)
self.l3 = nn.Linear(net_width, action_dim)
self.maxaction = maxaction
def forward(self, state):
a = paddle.tanh(self.l1(state))
a = paddle.tanh(self.l2(a))
a = paddle.tanh(self.l3(a)) * self.maxaction
return a
5.2 Critic网络
这里我们定义基本的Critic网络,每个网络中有两个Q-learning结构。
在整个TD3网络中,采用了Target Network结构,即定义两个Critic基本网络,使用相对稳定的目标网络输出值来构造Critic学习的Target Value从而保证Critic学习的稳定性。详见4.4节中的代码。
class Q_Critic(nn.Layer):
def __init__(self, state_dim, action_dim, net_width):
super(Q_Critic, self).__init__()
# Q1 architecture
self.l1 = nn.Linear(state_dim + action_dim, net_width)
self.l2 = nn.Linear(net_width, net_width)
self.l3 = nn.Linear(net_width, 1)
# Q2 architecture
self.l4 = nn.Linear(state_dim + action_dim, net_width)
self.l5 = nn.Linear(net_width, net_width)
self.l6 = nn.Linear(net_width, 1)
def forward(self, state, action):
sa = paddle.concat([state, action], 1)
q1 = F.relu(self.l1(sa))
q1 = F.relu(self.l2(q1))
q1 = self.l3(q1)
q2 = F.relu(self.l4(sa))
q2 = F.relu(self.l5(q2))
q2 = self.l6(q2)
return q1, q2
def Q1(self, state, action):
sa = paddle.concat([state, action], 1)
q1 = F.relu(self.l1(sa))
q1 = F.relu(self.l2(q1))
q1 = self.l3(q1)
return q1
5.3 Replay Buffer网络
在使用Q-learning算法的过程中,主要有两个问题:
- 交互得到的数据序列具有一定的相关性,而学习模型对训练样本的假设是独立同分布的。
- 交互样本的使用效率低,每次使用都需要获取一个batch的样本才能完成一次训练。
针对以上问题,提出了Replay Buffer网络结构来作为样本回放缓存区,其实就是一个样本收集再采样的过程,有限量的保存一定的数据并均匀随机的采样。这样做主要有两个优点:一、打消采样数据相关性。二、让数据分布变得更稳定。
class ReplayBuffer(object):
def __init__(self, state_dim, action_dim, max_size=int(1e6)):
self.max_size = max_size
self.ptr = 0
self.size = 0
self.state = np.zeros((max_size, state_dim))
self.action = np.zeros((max_size, action_dim))
self.reward = np.zeros((max_size, 1))
self.next_state = np.zeros((max_size, state_dim))
self.dead = np.zeros((max_size, 1))
self.device = paddle.device.set_device('gpu:0')
def add(self, state, action, reward, next_state, dead):
self.state[self.ptr] = state
self.action[self.ptr] = action
self.reward[self.ptr] = reward
self.next_state[self.ptr] = next_state
self.dead[self.ptr] = dead #0,0,0,...,1
self.ptr = (self.ptr + 1) % self.max_size
self.size = min(self.size + 1, self.max_size)
def sample(self, batch_size):
ind = np.random.randint(0, self.size, size=batch_size)
return (
paddle.to_tensor(self.state[ind],dtype='float32'),
paddle.to_tensor(self.action[ind],dtype='float32'),
paddle.to_tensor(self.reward[ind],dtype='float32'),
paddle.to_tensor(self.next_state[ind],dtype='float32'),
paddle.to_tensor(self.dead[ind],dtype='float32')
)
5.4 TD3网络搭建
至此,基本的各个网络组成部分都已经搭建完毕,可以开始组建TD3网络。
class TD3(object):
def __init__(
self,
env_with_Dead,
state_dim,
action_dim,
max_action,
gamma=0.99,
net_width=128,
a_lr=1e-4,
c_lr=1e-4,
Q_batchsize = 256
):
self.actor = Actor(state_dim, action_dim, net_width, max_action)
self.actor_optimizer = paddle.optimizer.Adam(parameters=self.actor.parameters(), learning_rate=a_lr)
self.actor_target = copy.deepcopy(self.actor)
self.q_critic = Q_Critic(state_dim, action_dim, net_width)
self.q_critic_optimizer = paddle.optimizer.Adam(parameters=self.q_critic.parameters(), learning_rate=c_lr)
self.q_critic_target = copy.deepcopy(self.q_critic)
self.env_with_Dead = env_with_Dead
self.action_dim = action_dim
self.max_action = max_action
self.gamma = gamma
self.policy_noise = 0.2*max_action
self.noise_clip = 0.5*max_action
self.tau = 0.005
self.Q_batchsize = Q_batchsize
self.delay_counter = -1
self.delay_freq = 1
def select_action(self, state):#only used when interact with the env
with paddle.no_grad():
state = paddle.to_tensor(state.reshape(1, -1),dtype='float32')
a = self.actor(state)
return a.cpu().numpy().flatten()
def train(self,replay_buffer):
self.delay_counter += 1
with paddle.no_grad():
s, a, r, s_prime, dead_mask = replay_buffer.sample(self.Q_batchsize)
noise = (paddle.randn(np.array(a).shape, dtype=a.dtype)*
self.policy_noise).clip(-self.noise_clip, self.noise_clip)
smoothed_target_a = (
self.actor_target(s_prime) + noise # Noisy on target action
).clip(-self.max_action, self.max_action)
# Compute the target Q value
target_Q1, target_Q2 = self.q_critic_target(s_prime, smoothed_target_a)
target_Q = paddle.minimum(target_Q1, target_Q2)
'''DEAD OR NOT'''
if self.env_with_Dead:
target_Q = r + (1 - dead_mask) * self.gamma * target_Q # env with dead
else:
target_Q = r + self.gamma * target_Q # env without dead
# Get current Q estimates
current_Q1, current_Q2 = self.q_critic(s, a)
# Compute critic loss
q_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)
# Optimize the q_critic
self.q_critic_optimizer.clear_grad()
q_loss.backward()
self.q_critic_optimizer.step()
if self.delay_counter == self.delay_freq:
# Update Actor
a_loss = -self.q_critic.Q1(s,self.actor(s)).mean()
self.actor_optimizer.clear_grad()
a_loss.backward()
self.actor_optimizer.step()
# Update the frozen target models
for param, target_param in zip(self.q_critic.parameters(), self.q_critic_target.parameters()):
target_param.set_value(self.tau * param + (1 - self.tau) * target_param)
for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
target_param.set_value(self.tau * param + (1 - self.tau) * target_param)
self.delay_counter = -1
def save(self,episode):
paddle.save(self.actor.state_dict(), "ppo_actor{}.pdparams".format(episode))
paddle.save(self.q_critic.state_dict(), "ppo_q_critic{}.pdparams".format(episode))
def load(self,episode):
self.actor.set_state_dict(paddle.load("ppo_actor{}.pdparams".format(episode)))
self.q_critic.set_state_dict(paddle.load("ppo_q_critic{}.pdparams".format(episode)))
6. 最终实现
在BipedalWalkerHardcore_v3环境中,摔倒、达到最大时间步和通关这三种情况触发done。根据贝尔曼方程,用于Critic更新的Target Value计算方式为 Q ( s , a ) = r + ( 1 − d o n e ) ∗ γ ∗ Q ( s n e x t , a n e x t ) Q(s,a)=r+(1-done)*gamma*Q(s_{next},a_{next}) Q(s,a)=r+(1−done)∗γ∗Q(snext,anext)。
可见在达到最大时间步和通关时候,会舍弃 Q ( s n e x t , a n e x t Q(s_{next},a_{next} Q(snext,anext,这是并不合理的。因为在这里我们相当于是人为终止提前终止了本轮训练,实际上如果环境继续运行下去 Q ( s n e x t , a n e x t Q(s_{next},a_{next} Q(snext,anext并不为0,只有当摔倒(Dead) 时才应为0。因此,我们需要对Done和Dead两种状态加以区分。在环境中,机器人摔倒后r=-100。故可以定义在r<-100时,done为True。由于正常情况下r在[-1,1]区间里,故设置r=-1,具体实现如下:
if r <= -100:
r = -1
done = True
else:
done = False
最终完整的训练和测试代码如下,并附有7500轮训练权重文件。其中当render和Loadmodel变量同时置为False时即为训练过程,同时置为True时即为测试过程。函数env.render()用于开启可视化运行过程。
import numpy as np
import paddle
import gym
from TD3 import TD3, ReplayBuffer
import matplotlib.pyplot as plt
from visualdl import LogWriter
device = paddle.device.get_device()
paddle.device.set_device('gpu:0')
def main(seed):
env_with_Dead = True
env = gym.make('BipedalWalkerHardcore-v3')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
max_action = float(env.action_space.high[0])
expl_noise = 0.25
print(' state_dim:', state_dim, ' action_dim:', action_dim, ' max_a:', max_action, ' min_a:', env.action_space.low[0])
render = False
Loadmodel = False
ModelIdex =3600 # model to load
random_seed = seed
Max_episode = 2000000
save_interval = 100 # interval to save model
if random_seed:
print("Random Seed: {}".format(random_seed))
paddle.seed(random_seed)
env.seed(random_seed)
np.random.seed(random_seed)
writer = LogWriter('./runs/exp')
kwargs = {
"env_with_Dead":env_with_Dead,
"state_dim": state_dim,
"action_dim": action_dim,
"max_action": max_action,
"gamma": 0.99,
"net_width": 200,
"a_lr": 1e-4,
"c_lr": 1e-4,
"Q_batchsize":256,
}
model = TD3(**kwargs)
if Loadmodel: model.load(ModelIdex)
replay_buffer = ReplayBuffer(state_dim, action_dim, max_size=int(1e6))
all_ep_r = []
for episode in range(Max_episode):
s, done = env.reset(), False
ep_r = 0
steps = 0
expl_noise *= 0.999
#test and trian
while not done:
steps+=1
if render:
a = model.select_action(s)
s_prime, r, done, info = env.step(a)
env.render()
else:
a = ( model.select_action(s) + np.random.normal(0, max_action * expl_noise, size=action_dim)
).clip(-max_action, max_action)
s_prime, r, done, info = env.step(a)
# Tricks for BipedalWalkerHardcore-v3
if r <= -100:
r = -1
replay_buffer.add(s, a, r, s_prime, True)
else:
replay_buffer.add(s, a, r, s_prime, False)
if replay_buffer.size > 2000: model.train(replay_buffer)
s = s_prime
ep_r += r
# save and plot
if episode%save_interval==0:
model.save(episode)
# plt.plot(all_ep_r)
# plt.savefig('seed{}-ep{}.png'.format(random_seed,episode+1))
# plt.clf()
# data record
# all_ep_r.append(ep_r)
if episode == 0: all_ep_r.append(ep_r)
else: all_ep_r.append(all_ep_r[-1]*0.9 + ep_r*0.1)
writer.add_scalar('s_ep_r', all_ep_r[-1], episode)
writer.add_scalar('ep_r', ep_r, episode)
writer.add_scalar('exploare', expl_noise, episode)
print('episode:', episode,'score:', ep_r, 'step:',steps , 'max:', max(all_ep_r))
env.close()
if __name__ == '__main__':
alar('s_ep_r', all_ep_r[-1], episode)
writer.add_scalar('ep_r', ep_r, episode)
writer.add_scalar('exploare', expl_noise, episode)
print('episode:', episode,'score:', ep_r, 'step:',steps , 'max:', max(all_ep_r))
env.close()
if __name__ == '__main__':
main(seed=102) # fix the random number seed
7. 收敛曲线
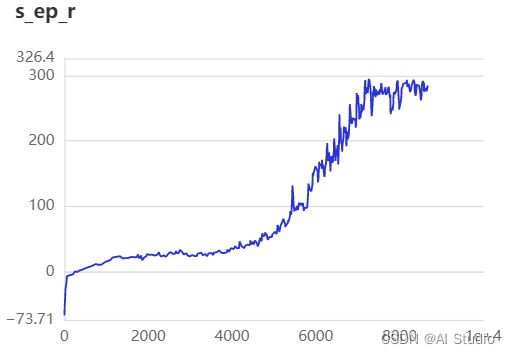
如图,大约在7100轮之后开始收敛。
在实际训练的过程中,发现对大障碍物的学习效果不佳,后期可以考虑在环境中适当增加其比例,以提高收敛速度。
此文章为搬运
原项目链接
最后
以上就是殷勤秋天最近收集整理的关于BipedalWalkerHardcore_v3游戏下基于TD3的强化学习BipedalWalkerHardcore_v3游戏下基于TD3的强化学习算法1. 项目准备2. 游戏环境介绍3. TD3网络介绍4. 效果演示5. 网络搭建6. 最终实现7. 收敛曲线的全部内容,更多相关BipedalWalkerHardcore_v3游戏下基于TD3的强化学习BipedalWalkerHardcore_v3游戏下基于TD3的强化学习算法1.内容请搜索靠谱客的其他文章。








发表评论 取消回复