matlab阶跃响应_状态空间模型及MATLAB指令计算

一. 基本概念强调

1. 时变控制系统

时变控制系统是指一个或多个系统参数会随着时间变化的系统。

2. 系统状态

系统状态是指表示系统的一组变量，只要知道了这组变量的当前取值情况、知道了输入信号和描述系统动态特征方程，就能完全确定系统未来的状态和输出响应。

3. 状态变量

状态变量描述了系统的当前状态。在给定输入激励和系统动态方程的条件下，状态变量还可以用于进一步确定系统的未来响应。

二. 基本知识回顾

1. 研究的意义：数字计算机的日益普及和简单易用，极大地方便了控制系统时域模型的求解，即研究动态系统的时域表示（微分方程表示），所谓的时域是指数学模型以时间尺度 t 为基本变量来描述系统及其相应。

2. 描述问题：描述系统的状态变量组（向量）并不是唯一的，存在多组不同的状态变量可供选择，通常的做法是，尽量选择易于测量的参数作为系统的状态变量。RLC网络中，选择电容电压和电感电流为状态变量组是合理的，因为电路所存储的能量可以表示为

，则初始状态时，状态变量组决定了该电路的初始储能。

3. 系统的状态空间模型包括了状态微分方程和输出方程。

状态微分方程的形式为

输出方程的形式为

对状态微分方程进行拉普拉斯变换，可得：

而通过微分方程的求解，可得状态微分方程的解为：

对比这两个式子，可知矩阵指数函数完全据诶U盾那个了系统的零输入响应，因此称

为系统的

4. 模型之间的转换

（1）由传递函数到状态空间表示

通过使用信号流图和框图模型，以及利用梅森公式，对传递函数进行变换，可以得到状态空间模型（相变量标准型模型、输入前馈标准型）；还有一种响应模态解耦模型，它是利用留数定理将传递函数展开，再利用信号流图得到。

传递函数为几阶，则信号流图中存在几个积分器，表示存在几个状态变量。

解耦形式的状态微分方程表明了系统具有n个不同的极点。这种形式的状态微分方程称为对角线标准型。具有互不相同的极点的系统总能够化为对角线标准型，否则只能华为块对角型，又称为约当标准型。

（2）由状态空间模型到传递函数模型

通过对状态空间方程进行拉普拉斯变换，可以得到系统实现的传递函数为

，其中的

表示状态转移矩阵。

5. 状态空间中的平衡点

在状态空间内，该系统的平衡点由条件

决定，这称为系统的平衡条件，其解则称为系统的平衡点。

三. 利用matlab软件分析状态空间模型

1. 状态空间方程的表述

函数tf能将状态空间模型转换为传递函数模型；

而函数ss能将传递函数转换为状态空间模型。

%   Convert G(s) = (2s^2+8s+6)/(s^3+8s^2+16s+6) 

%   to a state-space representation.

%

num=[2 8 6]; den=[1 8 16 6]; sys_tf=tf(num,den);

sys_ss=ss(sys_tf)

2. 矩阵指数函数

矩阵指数函数是指状态转移矩阵

，即有

,

使用函数expm(A)来求解给定时刻的状态转移矩阵；而函数exp(A)则是针对矩阵A中每个元素

分别求解

.

%   The state transition matrix for a given time, dt.

%

A=[0 -2;1 -3]; dt=0.2; 

Phi=expm(A*dt)

3. 系统的输出响应

使用函数lsim分别求解零初始条件和非零初始条件下的时间响应。

%   The time response for nonzero initial

%   conditions and zero input using lsim.

%

A=[0 -2;1 -3]; B=[2;0]; C=[1 0]; D=[0];

sys=ss(A,B,C,D);

x0=[1 1];

t=[0:0.01:1];

u=0*t;

[y,T,x]=lsim(sys,u,t,x0);

subplot(211), plot(T,x(:,1))

xlabel('Time (sec)'), ylabel('x_1')

subplot(212), plot(T,x(:,2))

xlabel('Time (sec)'), ylabel('x_2')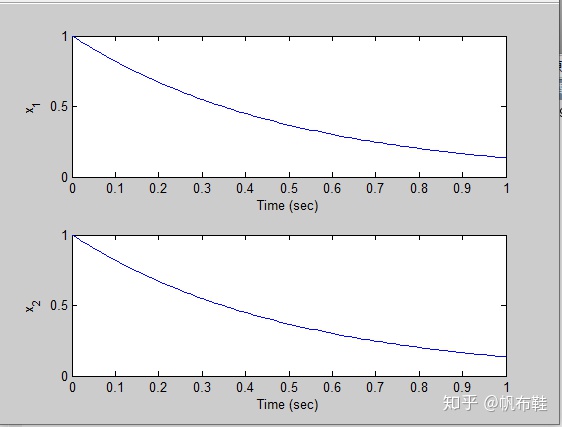

4. 循序渐进设计实例

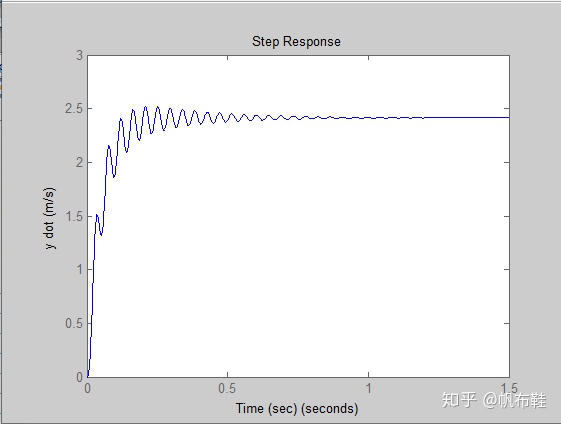
磁盘驱动器读取系统，在构建状态空间方程的情况下，使用step函数来求解系统的阶跃响应。

% Model Parameters

k=10; M1=0.02; M2=0.0005; b1=410e-03; b2=4.1e-03;

t=[0:0.001:1.5];

% State Space Model

A=[0 0 1 0;0 0 0 1;-k/M1 k/M1 -b1/M1 0; k/M2 -k/M2 0 -b2/M2];

B=[0;0;1/M1;0]; C=[0 0 0 1]; D=[0];

sys=ss(A,B,C,D);

% Simulated step Response

step(sys,t);

xlabel('Time (sec)'), ylabel('y dot (m/s)')