文章目录
- 0 前言
- 1 平面网格数据的生成
- 2 绘制三维曲面的函数
- 2.1 mesh函数和surf函数的一般召唤方式
- 2.2 其他召唤方式
- 2.3 mesh、surf函数的亲戚朋友
- 3.标准三维曲面
- 3.1 sphere函数-画个球
- 3.2 cylinder函数
- 3.3 peaks 函数-峰值曲面图
- 3.4 fmesh函数和fsurf函数-三个方程 两个自变量
- 4 结语
0 前言
本文是科学计算与MATLAB语言的专题四的第5小节总结笔记,并结合了自己一点的理解,看完本文,可以轻松利用MATLAB相关函数,画出漂亮的三维曲面。
1 平面网格数据的生成
在画三维曲面之前,需要将三维曲面对应的平面坐标存储起来,怎么存储呢?很简单有两种方法。
用矩阵X、Y分别存储每一个小矩形顶点的x坐标与y坐标,矩阵X、Y就是该矩形区域的xy平面网格坐标矩阵。
例如,在X-Y坐标平面生成一个由(2,6),(3,8)围成的网格坐标。
在MATLAB中,产生平面区域内的网格坐标矩阵有两种方法。
利用矩阵运算生成
x=2:6;
y=(3:8)';
X=ones(size(y))*x;
Y=y*ones(size(x));
X和Y相同位置上的元素,如
X
32
X_{32}
X32、
Y
32
Y_{32}
Y32是区域的第3行第2列网格点的坐标(3,5)。
利用meshgrid函数生成
这种方法是我们需要的!简洁,明了!
[X,Y]=meshgrid(x,y);
其中
参数x、y为向量,存储网格点坐标的X、Y为矩阵。
x=2:1:6;
y=(3:1:8)';
[X,Y]=meshgrid(x,y);
第3行命令生成的网格坐标矩阵X、Y与第一种得到的相同。
若根据每一个网格点上的x、y坐标求函数值z,则得到函数值矩阵Z。矩阵X、Y、Z中的各个列向量,对应于一条曲线数据点的坐标。
例1 绘制空间曲线。
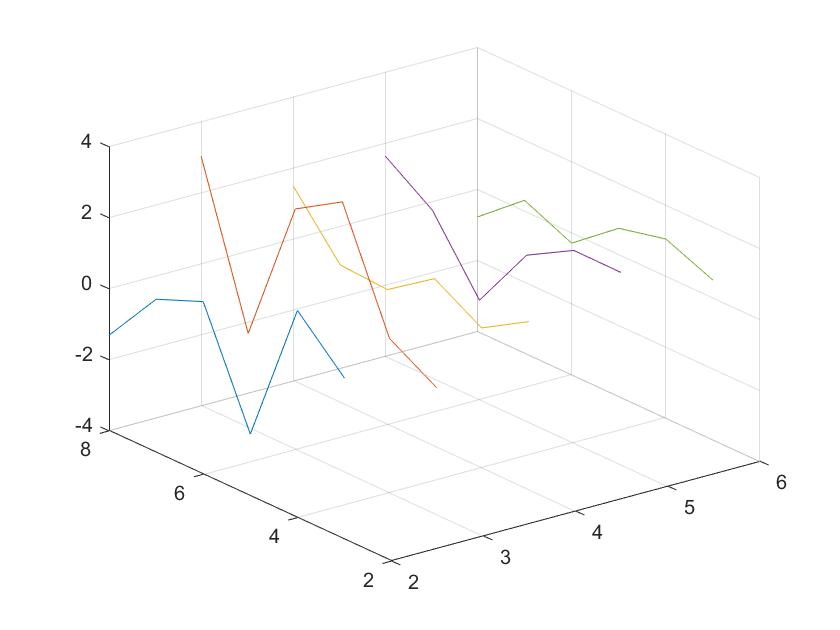
x = 2:6;
y = (3:8)';
[X, Y] = meshgrid(x, y);
Z = randn(size(X));
plot3(X,Y,Z)
grid on;
2 绘制三维曲面的函数
2.1 mesh函数和surf函数的一般召唤方式
mesh(x,y,z,c)
surf(x,y,z,c)
其中
x、y是网格坐标矩阵
z是网格点上的高度矩阵
c用于指定在不同高度下的曲面颜色
c省略时,颜色的设定正比于图形的高度。
例2 绘制三维曲面图
z
=
x
e
−
x
2
−
y
2
z=xe^{-x^2-y^2}
z=xe−x2−y2。
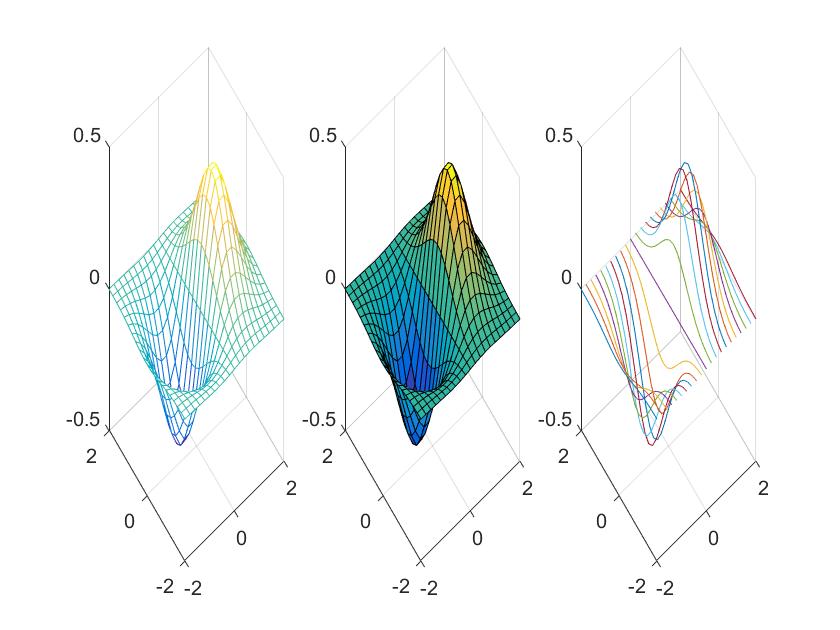
t = -2:0.2:2;
[X, Y] = meshgrid(t);
Z = X .* exp(-X.^2 - Y.^2);
subplot(1,3,1)
mesh(X,Y,Z);
subplot(1,3,2)
surf(X,Y,Z);
subplot(1,3,3)
plot3(X,Y,Z);
grid on
2.2 其他召唤方式
mesh(z,c)
surf(z,c)
当x、y省略时,z矩阵的第2维下标当作x轴坐标,z矩阵的第1维下标当作y轴坐标。
例如,绘制一个曲面。
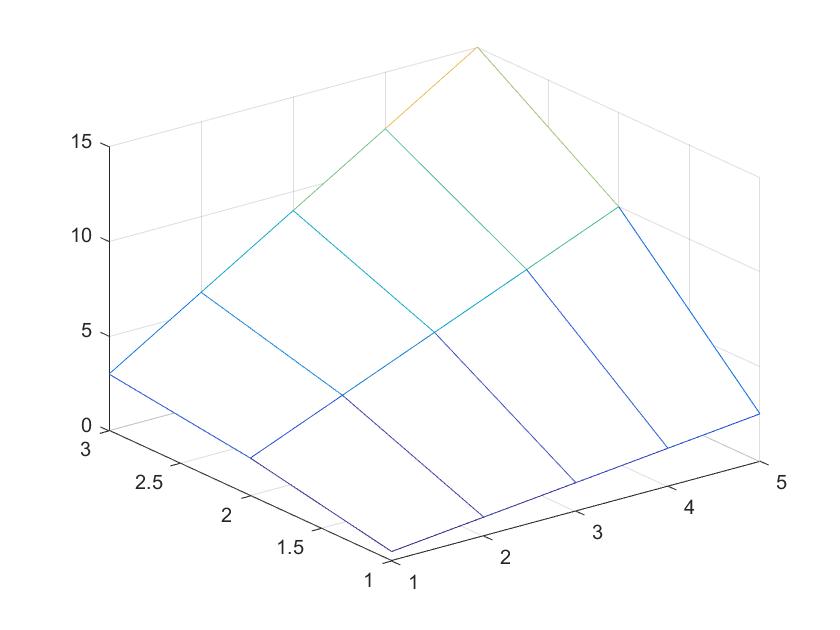
t=1:5;
z=[0.5*t;2*t;3*t];
mesh(z);
注意:z是一个为3行5列的矩阵,因此X轴坐标为1、2 、3 、4、5,Y轴坐标为1、2、3.
2.3 mesh、surf函数的亲戚朋友
| 函数名称 | 函数说明 |
|---|---|
| meshc | 带等高线的三维网格曲面 |
| meshz | 带底座的三维网格曲面 |
| surfc | 带等高线的曲面 |
| surfl | 带光照效果的曲面 |
例3 用4种方式绘制函数
z
=
(
x
−
1
)
2
+
(
y
−
2
)
2
−
1
z=(x−1)^2+(y−2)^2−1
z=(x−1)2+(y−2)2−1的曲面图。其中,
x
∈
[
0
,
2
]
,
y
∈
[
1
,
3
]
。
x∈[0,2],y∈[1,3]。
x∈[0,2],y∈[1,3]。
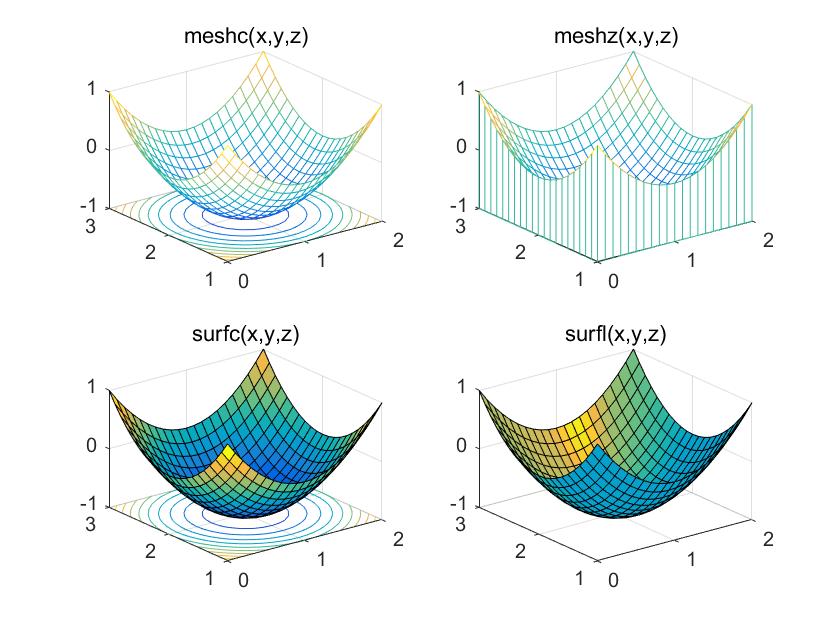
[x,y]=meshgrid(0:0.1:2,1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1);
meshc(x,y,z);title('meshc(x,y,z)')
subplot(2,2,2);
meshz(x,y,z);title('meshz(x,y,z)')
subplot(2,2,3);
surfc(x,y,z);title('surfc(x,y,z)')
subplot(2,2,4);
surfl(x,y,z); title('surfl(x,y,z)')
3.标准三维曲面
3.1 sphere函数-画个球
[x,y,z]=sphere(n)
产生3个(n+1)阶的方阵,采用这3个矩阵可以绘制出圆心位于原点、半径为1的单位球体。
3.2 cylinder函数
[x,y,z]=cylinder(R,n)
其中,参数R是一个向量,存放柱面各个等间隔高度上的半径,n表示在圆柱圆周上有n个间隔点,默认有20个间隔点。
例4 用cylinder函数分别绘制柱面、花瓶和圆锥面。
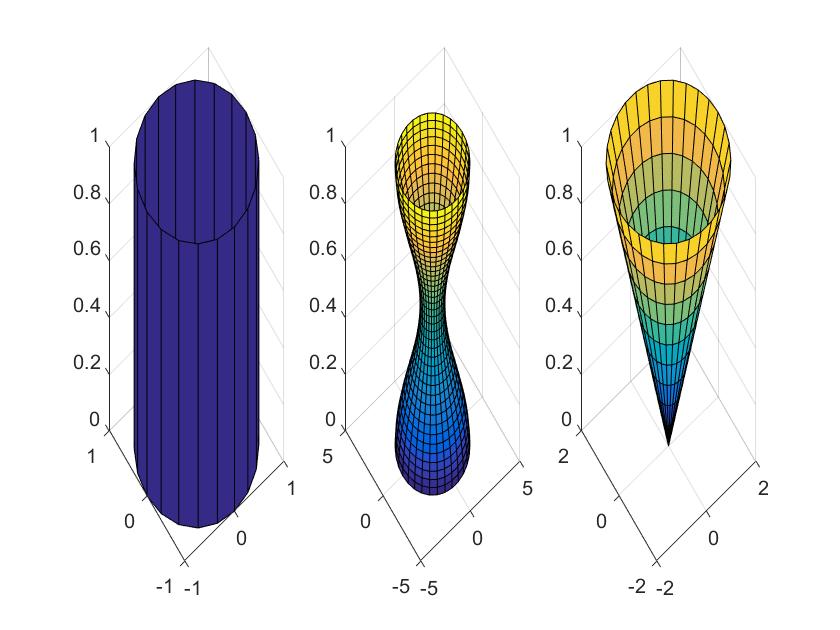
subplot(1,3,1);
[x,y,z]=cylinder;
surf(x,y,z);
subplot(1,3,2);
t=linspace(0,2*pi,40);
[x,y,z]= cylinder(2+cos(t),30);
surf(x,y,z);
subplot(1,3,3);
[x,y,z]= cylinder(0:0.2:2,30);
surf(x,y,z);
例5 用cylinder函数绘制两个相互垂直且直径相等的圆柱面的相交图形。
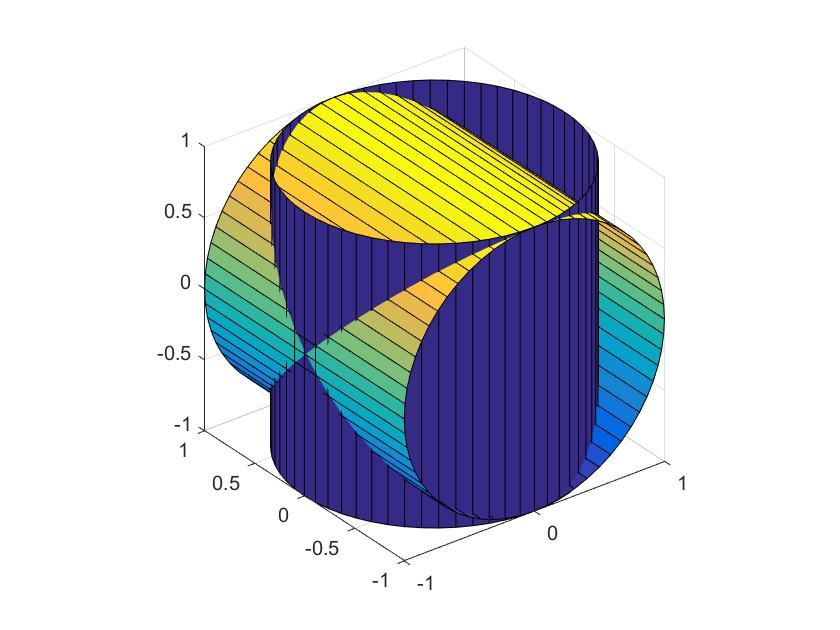
[x,y,z]= cylinder(1,60);
z=[-1*z(2,:);z(2,:)];
surf(x,y,z)
hold on
surf(y,z,x)
axis equal
3.3 peaks 函数-峰值曲面图
peaks函数的召唤方式:
peaks(n)返回一个 n×n 矩阵
peaks(V)返回一个 n×n 矩阵,其中 n = length(V)
peaks(x,y)在给定的 X 和 Y(必须大小相同)处计算 peaks 并返回大小相同的矩阵
peaks
具体使用方式参考官方文档。
多峰函数:
z
=
3
(
1
−
x
)
2
e
−
(
x
2
)
−
(
y
+
1
)
2
−
10
(
x
5
−
x
3
−
y
5
)
e
(
−
x
2
−
y
2
)
−
1
3
e
−
(
x
+
1
)
2
−
y
2
z = 3(1-x)^2e^{-(x^2) - (y+1)^2 }-10(frac{x}{5} - x^3 - y^5)e^{(-x^2-y^2})-frac{1}{3}e^{-(x+1)^2 - y^2}
z=3(1−x)2e−(x2)−(y+1)2−10(5x−x3−y5)e(−x2−y2)−31e−(x+1)2−y2
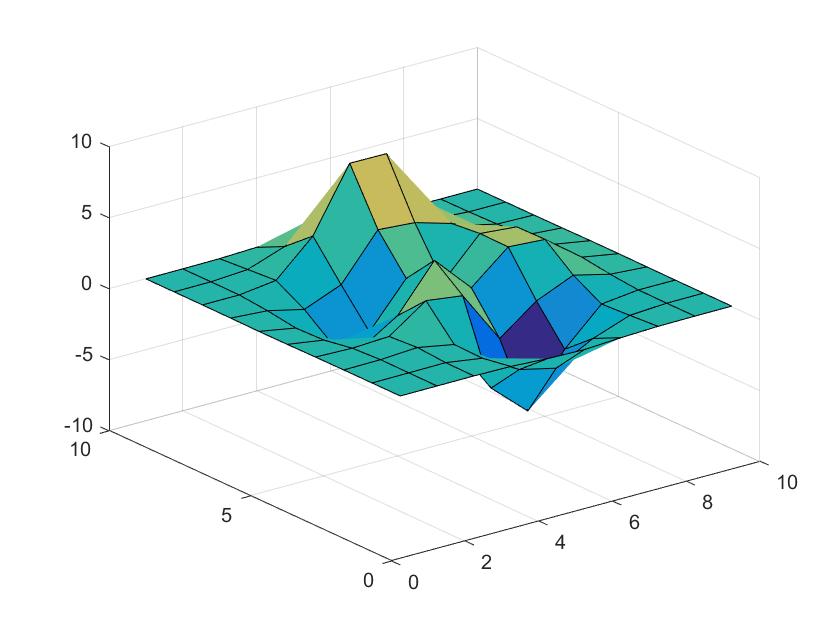
[x,y]=peaks(10);
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
- 1/3*exp(-(x+1).^2 - y.^2) ;
surf(z)
也可以通过以下命令绘制出此图。
figure
peaks(10)
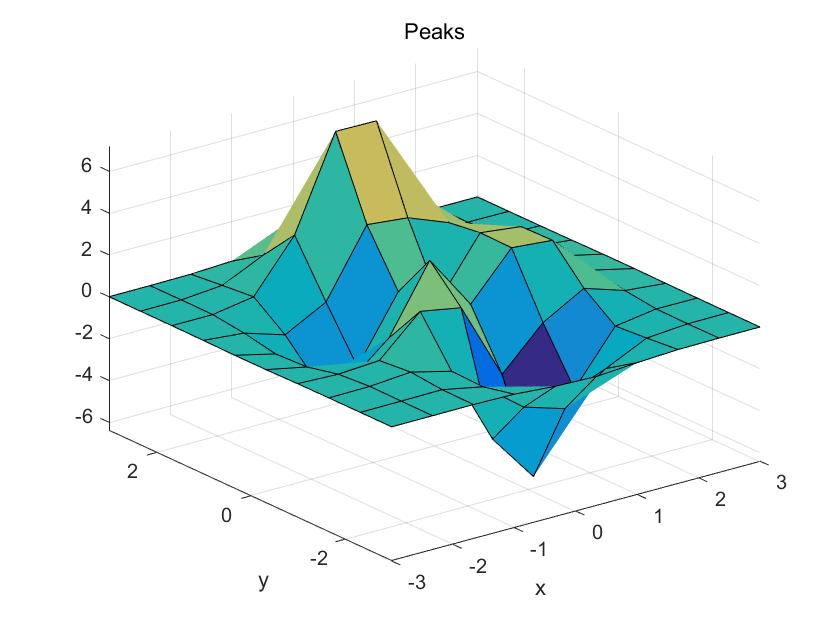
是不是一样?好像不是,坐标轴间隔、标注不一样呀,哈哈哈。目前我也不知道这个函数有啥用,不过好像很厉害的亚子!
3.4 fmesh函数和fsurf函数-三个方程 两个自变量
如果一个图形由三个参数方程决定,有两个自变量,那么可以使用fmesh函数和fsurf函数。
fmesh(funx,funy,funz,uvlims)
fsurf(funx,funy,funz,uvlims)
其中,funx、funy、funz代表定义曲面x、y、z坐标的函数,通常采用函数句柄的形式。
uwlims为funx、funy和funz的自变量的取值范围,用4元向量(umin,umax,vmin,vmaxd描述,默认为[-5,5,-5,5]。
例6 绘制螺旋曲面
{
x
=
u
s
i
n
v
y
=
−
u
c
o
s
v
,
(
−
5
≤
u
≤
5
,
−
5
≤
v
≤
2
)
z
=
v
left{ begin{aligned} x&=usinv\ y&=-ucosv,(-5 leq uleq5,-5leq vleq2)\ z&=v end{aligned}right.
⎩⎪⎨⎪⎧xyz=usinv=−ucosv,(−5≤u≤5,−5≤v≤2)=v
funx = @(u,v) u.*sin(v);
funy = @(u,v) -u.*cos(v);
funz = @(u,v) v;
fsurf(funx,funy,funz,[-5 5 -5 -2])%画出下半部分
hold on
fmesh(funx,funy,funz,[-5 5 -2 2])%画出上半部分
hold off
4 结语
您是否学会了呢?如果本文对您有帮助,可以点个赞哈,如有错误疑问,请您指出哈。
最后
以上就是想人陪小馒头最近收集整理的关于如何利用MATLAB函数绘制三维曲面?系统学习MATLAB三维曲面的绘制0 前言1 平面网格数据的生成2 绘制三维曲面的函数3.标准三维曲面4 结语的全部内容,更多相关如何利用MATLAB函数绘制三维曲面?系统学习MATLAB三维曲面的绘制0内容请搜索靠谱客的其他文章。








发表评论 取消回复