对算法的认识——逻辑回归

逻辑回归：找出一条直线来分类数据

逻辑回归虽然名字叫回归，却是属于分类算法，是通过Sigmoid函数将线性函数的结果映射到Sigmoid函数中，预估事件出现的概率并分类。
Sigmoid是归一化的函数，可以把连续数值转化为0到1的范围，提供了一种将连续型的数据离散化为离散型数据的方法。因此，逻辑回归从直观上来说是画出了一条分类线。位于分类线一侧的数据，概率>0.5,属于分类A；位于分类线另一侧的数据，概率0.5，属于分类B。

优点：

平滑、易于求导

缺点：

激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

Sigmoid函数由下列公式定义

$$S(x)=\frac{1}{1+e^{-x}}$$

其对x的导数可以用自身表示

$$S^{丶}(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=S(x)(1-S(x))$$

Sigmoid函数的图形如S曲线

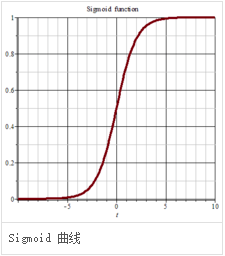
激活函数

在计算机网络中，一个节点的激活函数定义了该节点在给定的输入或输入的集合下的输出。标准的计算机芯片点了可以看作是根据输入得到开（1）或关（0）输出的数字电路激活函数。这与神经网络中的线性感知机的行为类似。然而，只有非线性激活函数才允许这种网络仅使用少量节点来计算非平凡问题。在人工神经网络中，这个功能也被称为传递函数。
Sigmoid函数和tanh函数是研究早期被广泛使用的2种激活函数。两者都为S型饱和函数。当Sigmoid函数输入的值趋于正无穷或负无穷时，梯度会趋近零，从而发生梯度弥散现象。sigmoid函数的输出恒为正值，不是以零为中心的，这会导致权值更新时只能朝一个方向更新，从而影响收敛速度。ranh激活函数时sigmoid函数的改进版，是以零为中心的对称函数，收敛速度快，不容易初恋loss值晃动，但是无法解释梯度弥散问题。2个函数的计算量都是指数级的，计算相对复杂。softsign函数是tanh函数的改进版，为S型饱和函数，以零为中心，值域为（-1，1）.

最后

以上就是清脆热狗为你收集整理的对算法的认识——逻辑回归的全部内容，希望文章能够帮你解决对算法的认识——逻辑回归所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。