前言

在上篇文章中我们介绍了下通信系统，按照信道中传输的是模拟信号还是数字信号，通信系统可分为模拟通信系统和数字通信系统；此外我们还介绍了广播、点-点、单工通信、半双工通信、全双工通信、并行传输、串行传输这些通信方式。在这篇文章里，

上文链接：《通信原理》（1）：初识通信原理

1.信息的度量：信息量

通信的目的在于传输信息，传输信息的多少可用“信息量”来进行衡量，信息量是对消息中“不确定性”的度量。
我们先来看个例子：

中国男子乒乓球队获得冠军
中国男子足球队获得冠军

显然，这两条信息发生的概率完全不同，一个接近1，一个几乎为0（狗头保命），那么哪条信息包含的信息量大呢？答案是第二条
消息中信息量与消息发生的概率相关，消息出现的概率越小，消息中包含的信息量就越大，且概率为零时（不可能发生事件）信息量为无穷大，概率为1时（必然事件）信息量为0。所以大家知道为什么第二条信息量更大了吧

现在我们用函数的方式来表示信息量I与消息出现概率P(x)之间的关系：

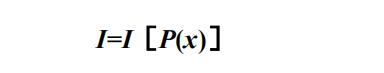
消息出现的概率越小，所含信息量越大，反之信息量越小：

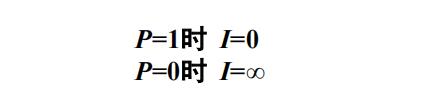
若干个互相独立事件构成的消息，其所含信息量等于各独立事件信息量的和

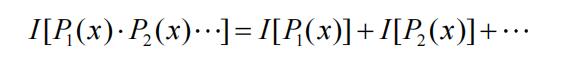
信息量I与消息出现的概率P(x)之间的关系为：

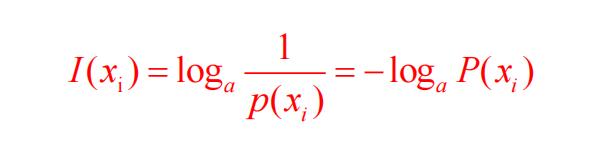
其中，信息量的单位与对数底数a有关：

• a=2时， 信息量的单位为比特(bit)
• a=e时， 信息量的单位为奈特(nit)
• a=10时，信息量的单位为叫哈特莱(hartley)

来看一道例题：
例：设不同进制离散信源，试计算二进制符号等概率(以相等的概率发送数字0或1)和多进制(M进制)等概率时每个符号的信息量

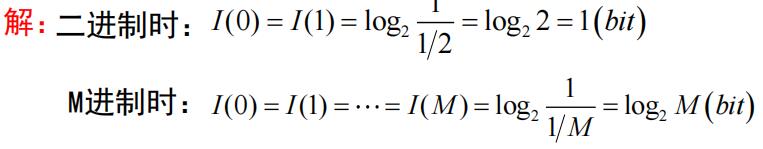
由此可以得到：

• 传送等概率的二进制波形之一的信息量为1比特
• 传送等概率的四进制波形之一的信息量为2比特
• 传送等概率的八进制波形之一的信息量为3比特

2.平均信息量

平均信息量等于各个符号信息量乘以各自出现的概率之和，描述每个符号所含信息量的统计平均值

设离散信源是一个由n个符号组成的符号集，每个符号xi(i=1,2,…,n)出现概率为P(xi)，且ΣP(xi)=1, 则平均信息量为：

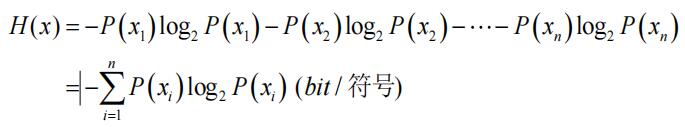
与热力学中的熵形式一样，所以称它为信息源的熵，单位为bit/符号

当离散信息源中的每个符号等概率出现时，而且各符号的出现为统计独立时，该信息源的信息量最大，此时最大熵（平均信息量）为：

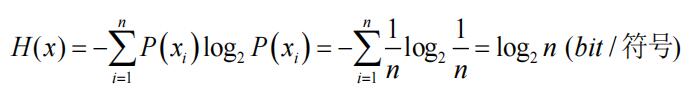
下面来看两道例题：
例1：设由5个符号组成的信息源，其相应概率为

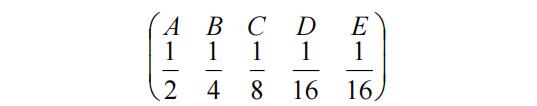
试求信源的平均信息量

解：利用平均信息量公式得：

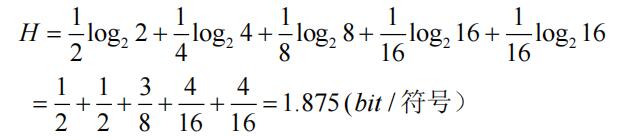
如果5个符号等概率出现时，平均信息量为：

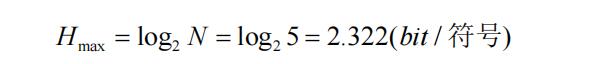
可以看到平均信息量的确更大

例2：设一离散信源由0， 1， 2， 3四个符号组成，它们出现的概率分别为3/8, 1/4, 1/4, 1/8，且每个符号的出现都是独立的。试求某消息201020130213001203210100321010023102002010312032100120210的信息量以及每个符号的平均信息量

解：
方法1：求消息中每个符号的个数，然后再乘以其信息量，最后求和

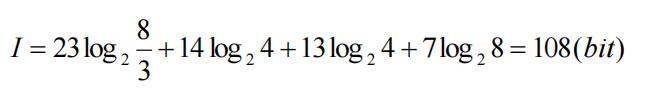
很明显，当符号数目巨大时，这种方法并不合适，一个一个的数工作量太大了

方法2：先求平均信息量，再乘以符号总数

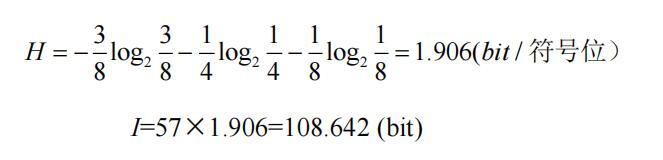
可见，两种算法结果有一定误差，但当消息很长时，用熵的概念来计算比较方便，随着消息序列长度的增加，两种计算误差将趋于零

3.连续信号的信息量和信源熵

对于连续消息，信息论中有一个重要结论，就是任何形式的待传信息都可以用二进制形式表示而不失主要内容。
抽样定理告诉我们：一个频带受限的连续信号，可以用每秒一定数目的抽
样值代替，而每个抽样值可以用若干个二进制脉冲序列来表示。
因此，以上信息量的定义和计算同样适用于连续信号

信源熵（平均信息量）：

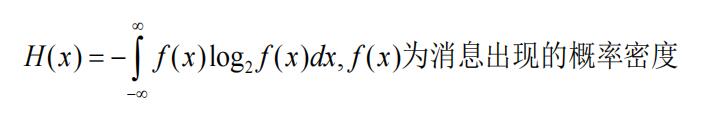
最后

以上就是稳重小懒虫为你收集整理的《通信原理》（2）：信息量及平均信息量前言1.信息的度量：信息量2.平均信息量3.连续信号的信息量和信源熵的全部内容，希望文章能够帮你解决《通信原理》（2）：信息量及平均信息量前言1.信息的度量：信息量2.平均信息量3.连续信号的信息量和信源熵所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。