一、信息量

信息是用不确定性的量度定义的。事件出现的概率小，不确定性越多，信息量就大，反之则少。

对于信息量与概率成负相关的理解：
当信源（产生消息的来源）中某一消息（事件）发生的不确定性越高，一旦它发生，并且被收信者接受，消除的不确定性也就越大，获得的信息也就越多。如果收信者接受到被干扰的消息，对一个消息（事件）发生的不确定性几乎没有消除，则收信者接受到的信息也就微乎其微。因此，获得信息量的大小与不确定性消除的大小有关，我们直观地将信息量定义为
    接受到了某消息（事件发生）所获得的信息量
    =不确定性减少量
    =（收到此消息前关于某事件发生的不确定性)-(收到此消息后关于某事件发生的不确定性）
举个例子：
2020年7月25日太阳从东边升起这个事件（必然事件），这件事发生前你知道了这件事情必然会发生（不确定性是0），发生后（不确定性也是0），不确定性减少量是0，因此我们所接受到的信息量是0。

上面几段话的总结：一个事件发生的概率越小，不确定性越大，（因为事件发生了，并且被接收了，事件发生所消除的不确定性就越大了），事件发生所带来的信息量也就越大。（可以看出来信息量与概率成负相关了）

香农提出了一个定量衡量信息量的公式：
$$\log \frac{1}{p}=-\log p$$

二、熵（entropy）

其实就是一个系统所有变量信息量的均值（期望），是衡量一个系统的稳定程度。当一个系统越不稳定，或者事件发生的不确定性越高，它的熵就越高。
公式：
对于离散变量：
$$H(X)=\sum _{x\in X}P(x)\log \frac{1}{P(x)}=-\sum _{x\in X}P(x)\log P(x)=-E\log P(X)$$

对于连续变量：
$$H(X)=\int P(x)\cdot \log \frac{1}{P(x)}dx$$

三、联合熵

多个联合变量的熵，也就是将熵的定义推广到多变量的范围。
$$H(X,Y)=\sum _{x\in X}\sum _{y\in Y}P(x,y)\log \frac{1}{P(x,y)}=-E\log P(X,Y)$$

四、条件熵

一个随机变量在给定的情况下，系统的熵，即假设在给定一个变量下，该系统信息量的期望。
$$\begin{array}{rl}H(Y\mid X)& =\sum _{x\in X}P(x)H(Y\mid X=x)\\ & =\sum _{x\in X}P(x)\left[\sum _{y\in Y}P(y\mid x)\log \frac{1}{P(y\mid x)}\right]\\ & =\sum _{x\in X}\sum _{y\in Y}P(x)P(y\mid x)\log \frac{1}{P(y\mid x)}\\ & =\sum _{x\in X}\sum _{y\in Y}P(x,y)\log \frac{1}{P(y\mid x)}\\ & =-E\log P(Y\mid X)\end{array}$$

五、相对熵（KL散度）

Kullback-Leibler Divergence，即K-L散度，是一种量化两种概率分布P和Q之间差异的方式，又叫相对熵。在概率学和统计学上，我们经常会使用一种更简单的、近似的分布来替代观察数据或太复杂的分布。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息量。

设p为观察得到的概率分布，q为另一分布来近似p，则p、q的K-L散度为：
$$D_{KL}(p\Vert q)=\sum _{i}p\left(x_i\right)\cdot \left[\log \frac{1}{q\left(x_i\right)}-\log \frac{1}{p\left(x_i\right)}\right]=\sum _{i}p\left(x_i\right)\cdot \log \frac{p\left(x_i\right)}{q\left(x_i\right)}$$
性质：

• 非负性
• 不对称性，即$KL(P\Vert Q)\ne KL(Q\Vert P)$

六、交叉熵(cross entropy)

也是用来衡量两个分布之间的差异性。
$$H_{CE}(p,q)=\sum _{i}p\left(x_i\right)\cdot \log \frac{1}{q\left(x_i\right)}$$
显然交叉熵是相对熵的第一部分，因为在通常情况下我们是已知第二部分​,即第二部分是常量，此时交叉熵和相对熵是一个线性关系，在考虑计算量的情况下，所以我们通常都用这部分交叉熵来做。

为什么在神经网络中使用交叉熵损失函数，而不是K-L散度？
K-L散度=交叉熵-熵，即 $D_{KL}(p\Vert q)=H(p,q)-H(p)$。
在神经网络所涉及到的范围内，$H(p)$不变，则$D_{KL}(p\Vert q)$等价$H(p,q)$。

七、JS散度(Jensen-Shannon divergence)

为了解决相对熵（KL散度不对称的问题），对KL散度进行变体。一般地，JS散度是对称的，其取值是 0 到 1 之间。
如果两个分布 P,Q 离得很远，完全没有重叠的时候，那么KL散度值是没有意义的，而JS散度值是一个常数（缺陷）。这在学习算法中是比较致命的，这就意味这这一点的梯度为 0，梯度消失了，无法更新。
$$\begin{array}{rl}{D}_{JS}(p\Vert q)& =0.5\ast \left[D_{KL}\left(p\Vert \frac{p+q}{2}\right)+D_{KL}\left(q\Vert \frac{p+q}{2}\right)\right]\\ & =0.5\ast \left[\sum _{i}p\left(x_i\right)\cdot \log \frac{2p\left(x_i\right)}{p\left(x_i\right)+q\left(x_i\right)}+\sum _{i}q\left(x_i\right)\cdot \log \frac{2q\left(x_i\right)}{p\left(x_i\right)+q\left(x_i\right)}\right]\end{array}$$

八、互信息

定义： 互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不确定性。
数学上的解释：
随机变量 X，另一个随机变量 Y，他们之间的互信息是：
$I(X;Y)=H(X)-H(X|Y)$
$H(X)$是X的信息熵
$H(Y)$是Y的信息熵
$H(X|Y)$是已知Y的条件下，X的信息熵
用图来表示是这样的：

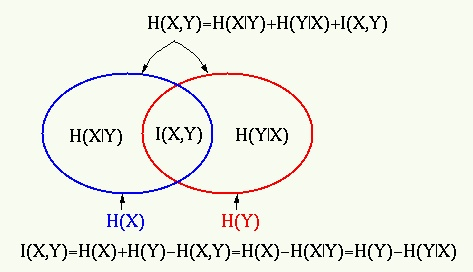
公式为：
$$\begin{array}{rl}I(X;Y)& ={\int }_X{\int }_{Y}P(X,Y)\log \frac{P(X,Y)}{P(X)P(Y)}\\ & ={\int }_X{\int }_{Y}P(X,Y)\log \frac{P(X,Y)}{P(X)}-{\int }_X{\int }_{Y}P(X,Y)\log P(Y)\\ & ={\int }_X{\int }_{Y}P(X)P(Y\mid X)\log P(Y\mid X)-{\int }_Y\log P(Y){\int }_{X}P(X,Y)\\ & ={\int }_{X}P(X){\int }_{Y}P(Y\mid X)\log P(Y\mid X)-{\int }_Y\log P(Y)P(Y)\\ & =-{\int }_{X}P(X)H(Y\mid X=x)+H(Y)\\ & =H(Y)-H(Y\mid X)\end{array}$$
当 X 和 Y 独立时，$P(X,Y)=P(X)P(Y)$，因此：$I(X;Y)=0$

参考资料：
https://blog.csdn.net/coolyuan/article/details/107564080
https://zhuanlan.zhihu.com/p/240676850
https://www.jianshu.com/p/43318a3dc715
https://blog.csdn.net/park_bomu/article/details/108829270

最后

以上就是饱满唇膏为你收集整理的信息论的一些基础概念一、信息量二、熵（entropy）三、联合熵四、条件熵五、相对熵（KL散度）六、交叉熵(cross entropy)七、JS散度(Jensen-Shannon divergence)八、互信息的全部内容，希望文章能够帮你解决信息论的一些基础概念一、信息量二、熵（entropy）三、联合熵四、条件熵五、相对熵（KL散度）六、交叉熵(cross entropy)七、JS散度(Jensen-Shannon divergence)八、互信息所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。