文章目录
- 前言
- 1. 算法相关基础
- 1.1 一阶倒立摆
- 1.2 二自由度车辆横向跟踪偏差模型
- 1.3 车辆横向跟踪偏差模型
- 1.4 车辆横向跟踪偏差倒车模型
- 1.5 轮胎侧偏角与侧偏刚度
- 1.6 LQR 线性二次型问题:
- 2. LQR代码解析
- 2.1 WriteHeaders(调试过程中的状态量)
- 2.2 LatController::LoadControlConf(读取横向配置中的参数)
- 2.3 LatController::InitializeFilters(低通滤波器)
- 2.4 LatController::Init(横向控制器的初始化)
- 2.5 LatController::LoadLatGainScheduler(横向增益的加载)
- 2.6 LatController::ComputeControlCommand(横向控制指令)
- 2.7 LatController::UpdateDrivingOrientation()
- 2.8 LatController::UpdateState
- 2.9 LatController::ComputeLateralErrors
- 3. 云平台实践教学
- 3.1 前置步骤
- 3.2 控制参数修改
前言
Apollo星火计划课程链接如下
星火计划2.0基础课:https://apollo.baidu.com/community/online-course/2
星火计划2.0专项课:https://apollo.baidu.com/community/online-course/12
1. 算法相关基础
1.1 一阶倒立摆
一阶倒立摆类似于车辆横向控制。
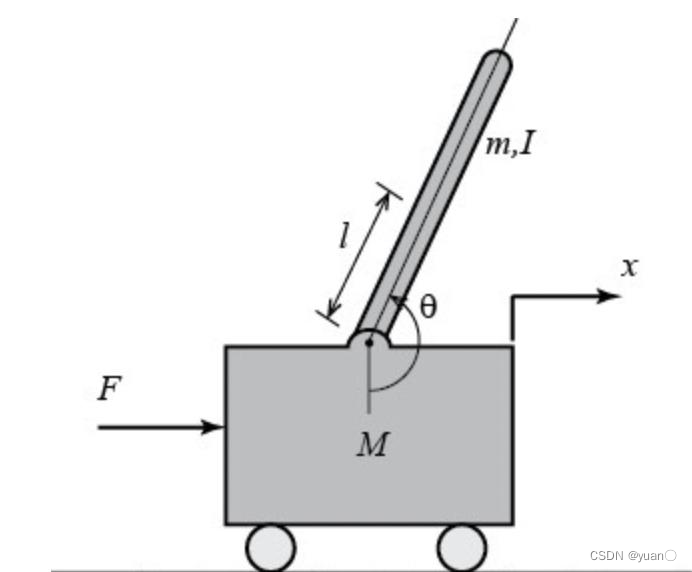
一阶倒立摆的相关内容可以参考以下两篇博客:
直线一级倒立摆数学建模与控制仿真
线性系统大作业——1.一阶倒立摆建模与控制系统设计
一阶倒立摆是一个非线性的控制问题,对其线性化后,通过调整零极点可以增强其稳定性。在车辆的控制上,可以通过状态空间的形式来表示车辆变化的过程。
对于一般的状态问题,我们给予以下表述:
x
˙
=
A
x
+
B
u
dot x=Ax+Bu
x˙=Ax+Bu
x
x
x在作用
u
u
u下,会形成一个新的状态
x
˙
dot x
x˙.
在Apollo代码中,将
x
x
x描述为偏差的形式,包括横向偏差、横向偏差的变化率以及轨迹朝向的偏差与变化率。
e
˙
r
r
=
A
e
r
r
+
B
u
dot err=Aerr+Bu
e˙rr=Aerr+Bu
1.2 二自由度车辆横向跟踪偏差模型
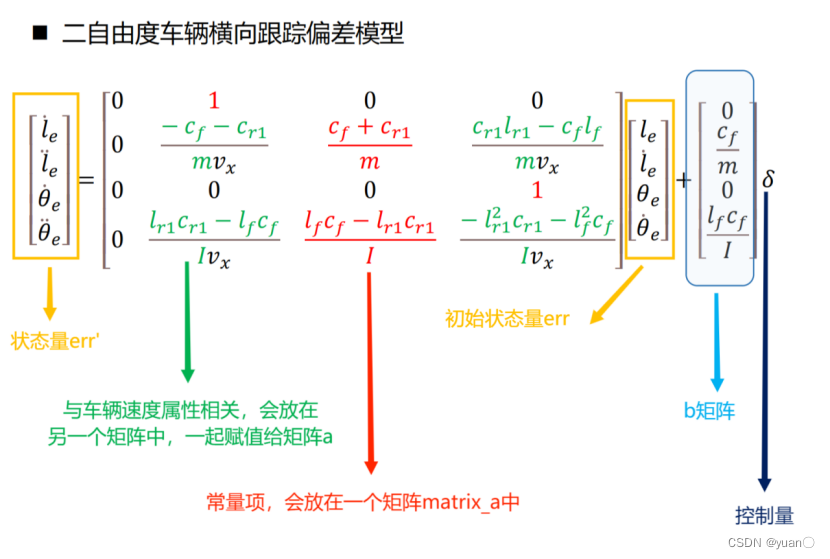
车辆动力学及控制的百度盘链接,想要进一步了解的读者可以下载。
链接:https://pan.baidu.com/s/14ScrNy6aho5vAIgRVEl9bQ?pwd=pk0x
提取码:pk0x

1.3 车辆横向跟踪偏差模型
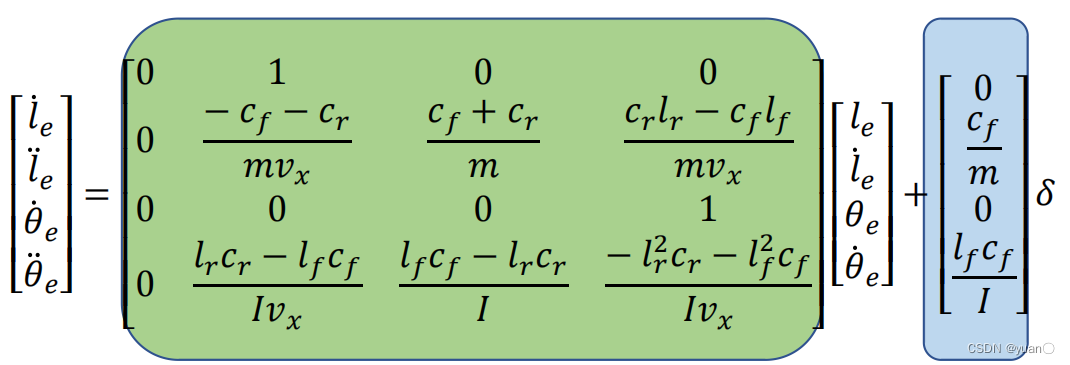
1.4 车辆横向跟踪偏差倒车模型
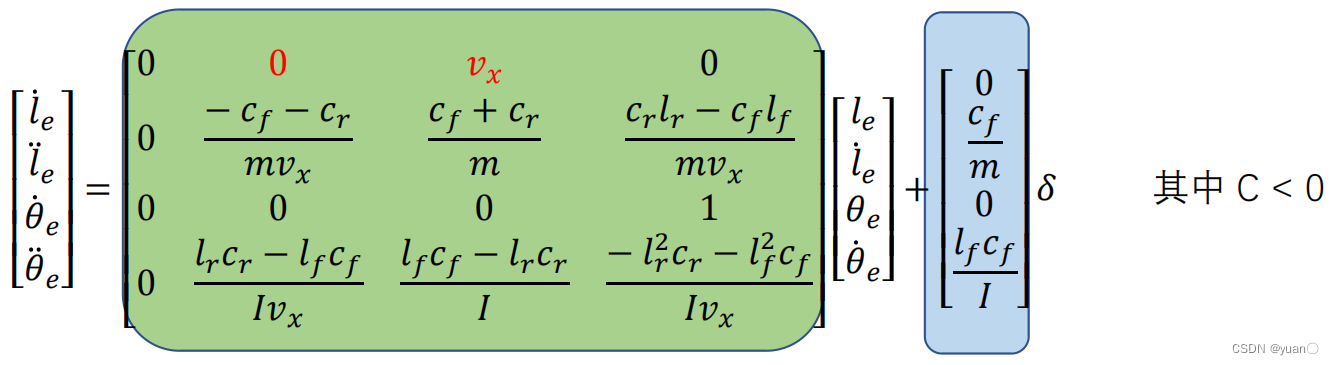
1.5 轮胎侧偏角与侧偏刚度
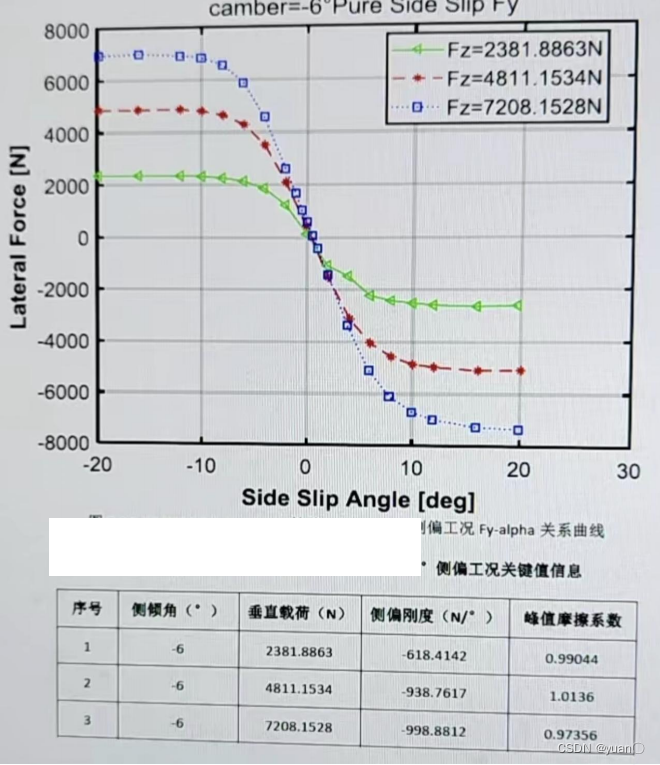

注意:此处需要将 N/°转化为N/rad
图中可以看出7000N载荷时侧偏刚度大约为 -1000N/°,转化后为-57295.78N/rad,所以apollo中155494.663为2倍结果,也就是两轮之和。
侧偏角与侧片偏刚度使用左手系,符号有出入。
1.6 LQR 线性二次型问题:
对于给定的一个系统,已知代价函数函数cost function,能否求解出一个控制序列使得整个控制系统稳定且使代价函数值达到最小。
对于一个线性离散系统
x
k
+
1
=
A
x
k
+
B
u
k
{x_{k + 1}} = A{x_k} + B{u_k}
xk+1=Axk+Buk 其拥有以下代价函数:
J
=
x
N
T
Q
x
N
+
∑
k
=
0
N
−
1
(
x
k
T
Q
x
k
+
u
k
T
R
u
k
)
J = x_N^TQ{x_N} + sumlimits_{k = 0}^{N - 1} {(x_k^TQ{x_k} + u_k^TR{u_k})}
J=xNTQxN+k=0∑N−1(xkTQxk+ukTRuk) LQR 线性二次型问题就是求解最优控制序列
u
u
u,使得代价函数
J
J
J达到最小.
L
L
L——线性系统,若非线性则需将其线性化
Q
Q
Q——代价函数,限定其为二次型
R
R
R——调节器
L
Q
R
LQR
LQR目的——既能满足控制目标的要求,又能使输入能量达到最小。
∑
k
=
0
N
−
1
(
x
k
T
Q
x
k
+
u
k
T
R
u
k
)
sumlimits_{k = 0}^{N - 1} {(x_k^TQ{x_k} + u_k^TR{u_k})}
k=0∑N−1(xkTQxk+ukTRuk) 通过累计求和,使得代价函数
J
J
J达到一个最小值,当
N
N
N趋向于无穷时,状态量
x
k
x_k
xk会趋向于0,即系统趋于稳定,同时由于系统趋于稳定,
u
k
u_k
uk也会趋于0.也就是说,随着时间推移,我们需要对系统施加的控制量就会越来越小。
求解代价函数
J
J
J最小值的方法有哈密尔顿方程、拉格朗日法等。
无论是哪种求解方法,最终的目的是求解出最优的状态反馈控制器:
u
k
=
−
K
k
x
k
{u_k} = - {K_k}{x_k}
uk=−Kkxk 其中反馈增益矩阵K为:
K
k
=
(
R
+
B
T
P
k
+
1
B
)
−
1
(
B
T
P
k
+
1
A
+
N
T
)
{K_k} = {(R + {B^T}{P_{k + 1}}B)^{ - 1}}({B^T}{P_{k + 1}}A + {N^T})
Kk=(R+BTPk+1B)−1(BTPk+1A+NT) 通过
K
K
K我们可以求解出在当前状态下,输出的控制量的大小。
上式中,
P
P
P为连续时间黎卡提方程的解,可以通过迭代求解得到:
P
k
−
1
=
A
T
P
k
A
−
(
A
T
P
k
B
+
N
)
(
R
+
B
T
P
k
B
)
−
1
(
B
T
P
k
A
+
N
T
)
+
Q
{P_{k - 1}} = {A^T}{P_k}A - ({A^T}{P_k}B + N){(R + {B^T}{P_k}B)^{ - 1}}({B^T}{P_k}A + {N^T}) + Q
Pk−1=ATPkA−(ATPkB+N)(R+BTPkB)−1(BTPkA+NT)+Q注意:从终端条件
P
N
=
Q
P_N=Q
PN=Q 开始迭代
基于偏差的形式构建状态转移方程为
e
r
r
k
+
1
=
A
e
r
r
k
+
B
u
k
+
C
θ
˙
r
er{r_{k + 1}} = Aer{r_k} + B{u_k} + C{dot theta _r}
errk+1=Aerrk+Buk+Cθ˙r 在代码中,黎卡提方程
P
k
−
1
=
A
T
P
k
A
−
(
A
T
P
k
B
+
N
)
(
R
+
B
T
P
k
B
)
−
1
(
B
T
P
k
A
+
N
T
)
+
Q
{P_{k - 1}} = {A^T}{P_k}A - ({A^T}{P_k}B + N){(R + {B^T}{P_k}B)^{ - 1}}({B^T}{P_k}A + {N^T}) + Q
Pk−1=ATPkA−(ATPkB+N)(R+BTPkB)−1(BTPkA+NT)+Q如下图所示
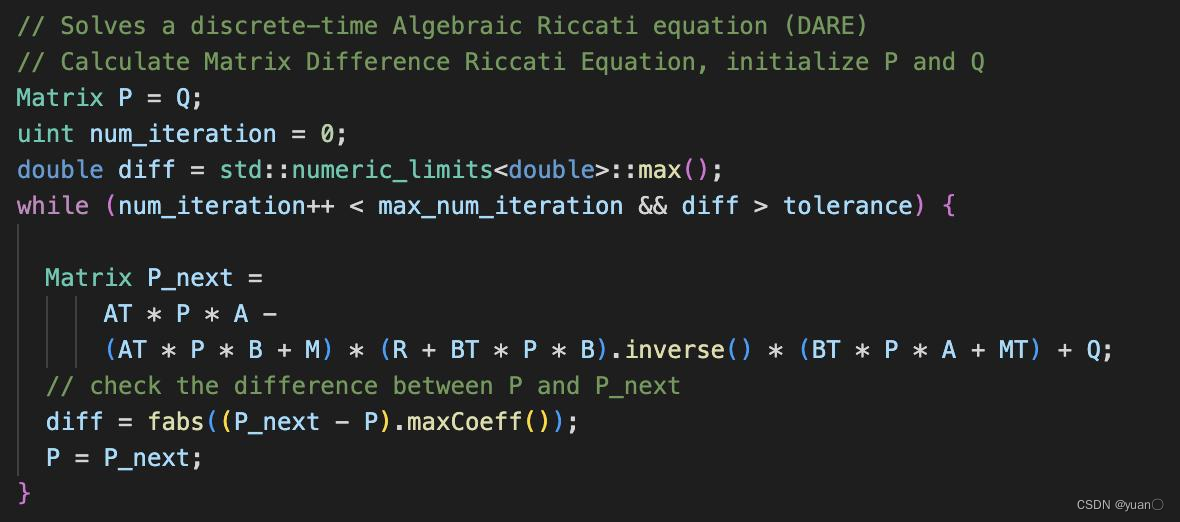
其中
K
k
=
(
R
+
B
T
P
k
+
1
B
)
−
1
(
B
T
P
k
+
1
A
+
N
T
)
{K_k} = {(R + {B^T}{P_{k + 1}}B)^{ - 1}}({B^T}{P_{k + 1}}A + {N^T})
Kk=(R+BTPk+1B)−1(BTPk+1A+NT)表示如下:![]()
我们使用LQR计算出的控制量
u
k
=
−
K
k
∗
e
r
r
k
{u_k} = - {K_k}*{err_k}
uk=−Kk∗errk,难以将车辆维持在车道中心线上,实际上,道路存在的曲率等特征会影响到系统,从而产生一定的稳态误差
e
r
r
k
+
1
=
A
e
r
r
k
+
B
u
k
+
C
θ
˙
r
er{r_{k + 1}} = Aer{r_k} + B{u_k} + C{dot theta _r}
errk+1=Aerrk+Buk+Cθ˙r。
此时我们引入前馈控制量
δ
f
delta_f
δf 作用到输出上,减少控制系统的稳态误差
u
k
=
−
K
k
∗
e
r
r
k
+
δ
f
{u_k} = - {K_k}*{err_k}+delta_f
uk=−Kk∗errk+δf 车辆横向跟踪偏差模型如下所示: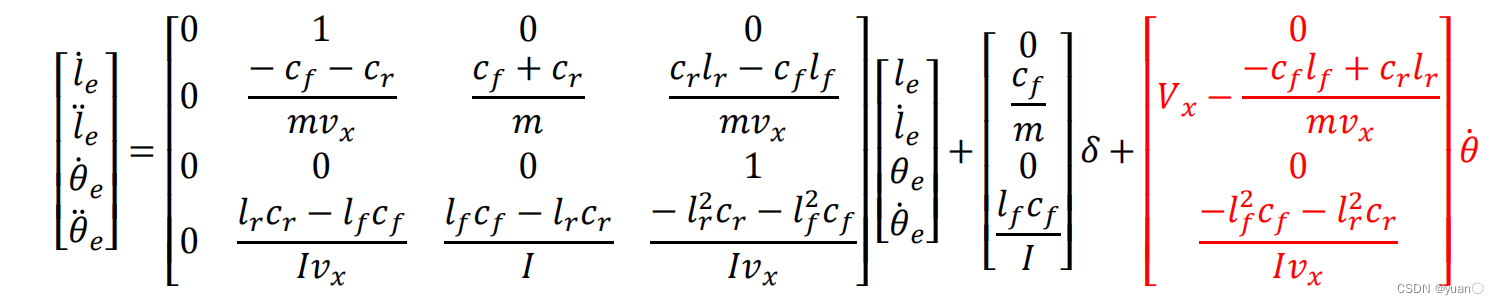
《车辆动力学及控制》第三章中提出稳态误差求解公式: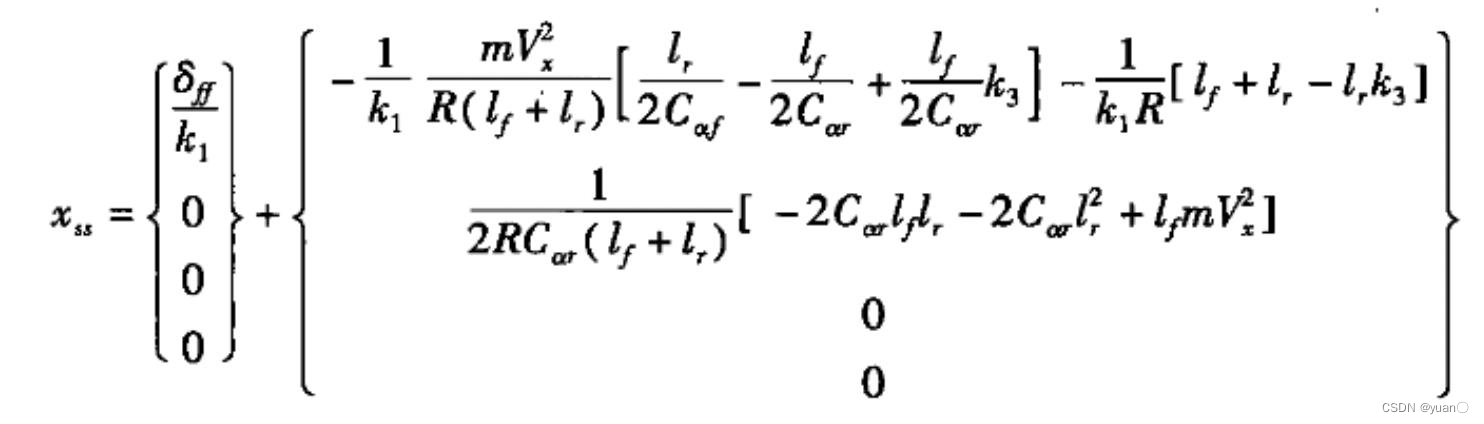
考虑侧偏刚度符号问题,适配到Apollo动力学模型得到如下公式及实现: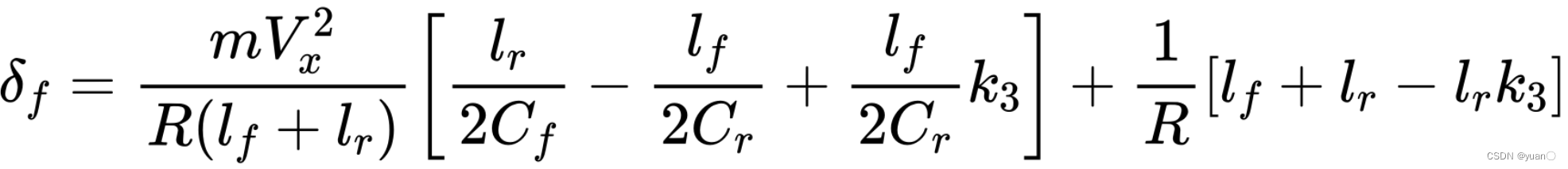
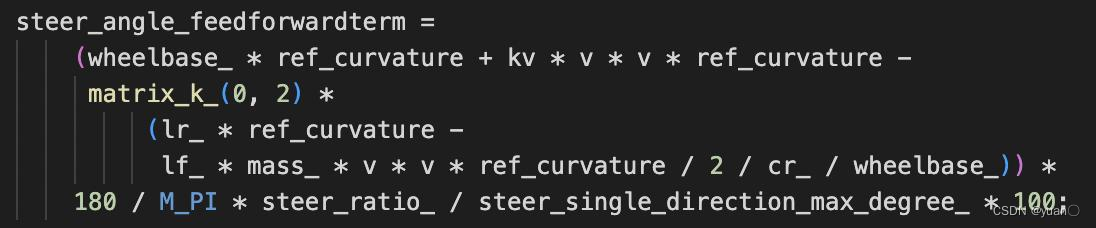
其中kv为不足转向斜率.
2. LQR代码解析
2.1 WriteHeaders(调试过程中的状态量)
//保存到日志中的状态量
void WriteHeaders(std::ofstream &file_stream) {
file_stream << "current_lateral_error," //当前横向偏差
<< "current_ref_heading," //当前参考航向
<< "current_heading," //当前航向
<< "current_heading_error," //当前航向偏差
<< "heading_error_rate," //航向误差变化率
<< "lateral_error_rate," //横向误差变化率
<< "current_curvature," //当前曲率
<< "steer_angle," //方向盘转角
<< "steer_angle_feedforward," //前馈控制计算输出
<< "steer_angle_lateral_contribution," //k矩阵中横向偏差计算结果分量
<< "steer_angle_lateral_rate_contribution," //k矩阵中横向偏差率计算结果分量
<< "steer_angle_heading_contribution," //k矩阵中航向偏差计算结果分量
<< "steer_angle_heading_rate_contribution," //k矩阵中航向偏差率计算结果分量
<< "steer_angle_feedback," //LQR计算出的方向盘控制量
<< "steering_position," //当前底盘方向盘状态
<< "v" << std::endl; //车速
}
控制结果未到达期望,可以首先查看当前底盘方向盘状态steering_position与方向盘转角的输出steer_angle是否吻合。若吻合(两者相近),则说明控制的输出量偏小,可以通过适当调节横向偏差及其变化率与航向偏差及其变化率(调节的是权重)。再者,可以参考k矩阵相关的四个参数。
2.2 LatController::LoadControlConf(读取横向配置中的参数)
// 读取横向配置中的参数
bool LatController::LoadControlConf(const ControlConf *control_conf) {
if (!control_conf) {
AERROR << "[LatController] control_conf == nullptr";
return false;
}
vehicle_param_ =
common::VehicleConfigHelper::Instance()->GetConfig().vehicle_param(); // 加载车辆配置参数
ts_ = control_conf->lat_controller_conf().ts(); // 异常检查,若ts小于0,则为无效的时间间隔
if (ts_ <= 0.0) {
AERROR << "[MPCController] Invalid control update interval.";
return false;
}
cf_ = control_conf->lat_controller_conf().cf(); // 前两轮轮胎侧偏刚度
cr_ = control_conf->lat_controller_conf().cr(); // 后两轮轮胎侧偏刚度
preview_window_ = control_conf->lat_controller_conf().preview_window();
lookahead_station_low_speed_ = // 低速前行预瞄距离,修复不同速度下的参考点的对准问题
control_conf->lat_controller_conf().lookahead_station();
lookback_station_low_speed_ = // 低速倒车预瞄距离
control_conf->lat_controller_conf().lookback_station();
lookahead_station_high_speed_ = // 高速倒车预瞄距离
control_conf->lat_controller_conf().lookahead_station_high_speed();
lookback_station_high_speed_ = // 高速前行预瞄距离
control_conf->lat_controller_conf().lookback_station_high_speed();
wheelbase_ = vehicle_param_.wheel_base(); // 轴距
steer_ratio_ = vehicle_param_.steer_ratio(); // 转向比例
steer_single_direction_max_degree_ = // 最大方向转角
vehicle_param_.max_steer_angle() / M_PI * 180;
max_lat_acc_ = control_conf->lat_controller_conf().max_lateral_acceleration();// 最大侧向加速度
low_speed_bound_ = control_conf_->lon_controller_conf().switch_speed(); // 横向配置低速时的速度约束
low_speed_window_ =
control_conf_->lon_controller_conf().switch_speed_window();
const double mass_fl = control_conf->lat_controller_conf().mass_fl(); // 车辆左前质量
const double mass_fr = control_conf->lat_controller_conf().mass_fr();
const double mass_rl = control_conf->lat_controller_conf().mass_rl();
const double mass_rr = control_conf->lat_controller_conf().mass_rr();
const double mass_front = mass_fl + mass_fr; // 车辆前悬质量
const double mass_rear = mass_rl + mass_rr;
mass_ = mass_front + mass_rear; // 车辆总质量
lf_ = wheelbase_ * (1.0 - mass_front / mass_); // 车辆前悬长度
lr_ = wheelbase_ * (1.0 - mass_rear / mass_); // 车辆后悬长度
// moment of inertia
iz_ = lf_ * lf_ * mass_front + lr_ * lr_ * mass_rear; // 车辆转动惯量
lqr_eps_ = control_conf->lat_controller_conf().eps(); // LQR优化的最小精度0.01,停止条件为1
lqr_max_iteration_ = control_conf->lat_controller_conf().max_iteration(); // LQR最大迭代次数
query_relative_time_ = control_conf->query_relative_time(); // 相对时间,机构延时(大约500ms的延时)
minimum_speed_protection_ = control_conf->minimum_speed_protection(); // 最小速度
return true;
}
2.3 LatController::InitializeFilters(低通滤波器)
// 低通滤波器 去除高频噪声 效果同积分器
void LatController::InitializeFilters(const ControlConf *control_conf) {
// Low pass filter
std::vector<double> den(3, 0.0);
std::vector<double> num(3, 0.0);
common::LpfCoefficients(
ts_, control_conf->lat_controller_conf().cutoff_freq(), &den, &num);
digital_filter_.set_coefficients(den, num);
// 偏差均值滤波 防止突变
lateral_error_filter_ = common::MeanFilter(static_cast<std::uint_fast8_t>(
control_conf->lat_controller_conf().mean_filter_window_size()));
heading_error_filter_ = common::MeanFilter(static_cast<std::uint_fast8_t>(
control_conf->lat_controller_conf().mean_filter_window_size()));
}
2.4 LatController::Init(横向控制器的初始化)
// 控制器初始化,动力学模型初始化
Status LatController::Init(std::shared_ptr<DependencyInjector> injector,
const ControlConf *control_conf) {
control_conf_ = control_conf;
injector_ = injector;
if (!LoadControlConf(control_conf_)) {
AERROR << "failed to load control conf";
return Status(ErrorCode::CONTROL_COMPUTE_ERROR,
"failed to load control_conf");
}
// Matrix init operations.
const int matrix_size = basic_state_size_ + preview_window_; // 矩阵大小默认为基本状态大小 4维
matrix_a_ = Matrix::Zero(basic_state_size_, basic_state_size_); // 矩阵a常量
matrix_ad_ = Matrix::Zero(basic_state_size_, basic_state_size_); // 离散化矩阵A
matrix_adc_ = Matrix::Zero(matrix_size, matrix_size);
/*
A matrix (Gear Drive)
[0.0, 1.0, 0.0, 0.0;
0.0, (-(c_f + c_r) / m) / v, (c_f + c_r) / m,
(l_r * c_r - l_f * c_f) / m / v;
0.0, 0.0, 0.0, 1.0;
0.0, ((lr * cr - lf * cf) / i_z) / v, (l_f * c_f - l_r * c_r) / i_z,
(-1.0 * (l_f^2 * c_f + l_r^2 * c_r) / i_z) / v;]
*/
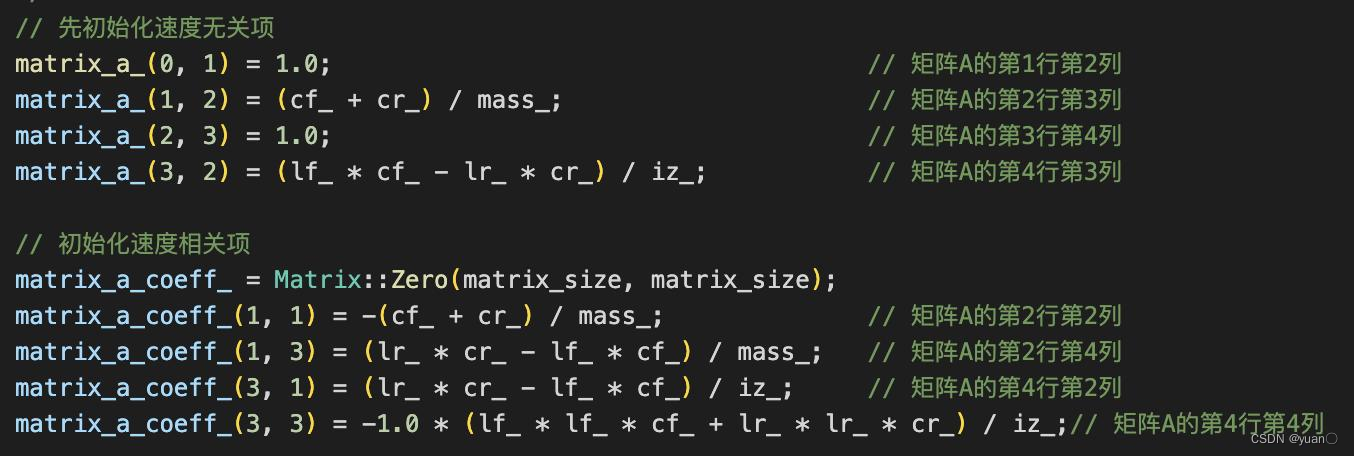
// 矩阵a速度无关项
matrix_a_(0, 1) = 1.0;
matrix_a_(1, 2) = (cf_ + cr_) / mass_;
matrix_a_(2, 3) = 1.0;
matrix_a_(3, 2) = (lf_ * cf_ - lr_ * cr_) / iz_;
// 矩阵a速度相关项
matrix_a_coeff_ = Matrix::Zero(matrix_size, matrix_size);
matrix_a_coeff_(1, 1) = -(cf_ + cr_) / mass_;
matrix_a_coeff_(1, 3) = (lr_ * cr_ - lf_ * cf_) / mass_;
matrix_a_coeff_(3, 1) = (lr_ * cr_ - lf_ * cf_) / iz_;
matrix_a_coeff_(3, 3) = -1.0 * (lf_ * lf_ * cf_ + lr_ * lr_ * cr_) / iz_;
/*
b = [0.0, c_f / m, 0.0, l_f * c_f / i_z]^T
*/
matrix_b_ = Matrix::Zero(basic_state_size_, 1);
matrix_bd_ = Matrix::Zero(basic_state_size_, 1);
matrix_bdc_ = Matrix::Zero(matrix_size, 1);
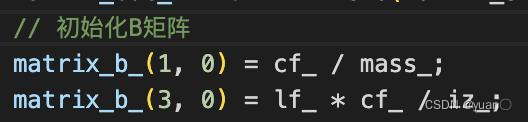
// 矩阵b
matrix_b_(1, 0) = cf_ / mass_;
matrix_b_(3, 0) = lf_ * cf_ / iz_;
matrix_bd_ = matrix_b_ * ts_;
// LQR权重矩阵
matrix_state_ = Matrix::Zero(matrix_size, 1);
matrix_k_ = Matrix::Zero(1, matrix_size); //反馈矩阵
matrix_r_ = Matrix::Identity(1, 1);
matrix_q_ = Matrix::Zero(matrix_size, matrix_size);
int q_param_size = control_conf_->lat_controller_conf().matrix_q_size();
int reverse_q_param_size =
control_conf_->lat_controller_conf().reverse_matrix_q_size();
if (matrix_size != q_param_size || matrix_size != reverse_q_param_size) {
const auto error_msg = absl::StrCat(
"lateral controller error: matrix_q size: ", q_param_size,
"lateral controller error: reverse_matrix_q size: ",
reverse_q_param_size,
" in parameter file not equal to matrix_size: ", matrix_size);
AERROR << error_msg;
return Status(ErrorCode::CONTROL_COMPUTE_ERROR, error_msg);
}
for (int i = 0; i < q_param_size; ++i) {
matrix_q_(i, i) = control_conf_->lat_controller_conf().matrix_q(i);
}
matrix_q_updated_ = matrix_q_;
InitializeFilters(control_conf_); // 初始化滤波器 均值滤波 低通数字滤波器
auto &lat_controller_conf = control_conf_->lat_controller_conf();
LoadLatGainScheduler(lat_controller_conf);
LogInitParameters();
// 滞后超前控制器
enable_leadlag_ = control_conf_->lat_controller_conf()
.enable_reverse_leadlag_compensation();
if (enable_leadlag_) {
leadlag_controller_.Init(lat_controller_conf.reverse_leadlag_conf(), ts_);
}
// 模型参考自适应控制
enable_mrac_ =
control_conf_->lat_controller_conf().enable_steer_mrac_control();
if (enable_mrac_) {
mrac_controller_.Init(lat_controller_conf.steer_mrac_conf(),
vehicle_param_.steering_latency_param(), ts_);
}
enable_look_ahead_back_control_ =
control_conf_->lat_controller_conf().enable_look_ahead_back_control();
return Status::OK();
}
2.5 LatController::LoadLatGainScheduler(横向增益的加载)
void LatController::LoadLatGainScheduler(
const LatControllerConf &lat_controller_conf) {
const auto &lat_err_gain_scheduler = // 不同速度下的横向偏差增益
lat_controller_conf.lat_err_gain_scheduler();
const auto &heading_err_gain_scheduler = // 不同速度下的航向偏差增益
lat_controller_conf.heading_err_gain_scheduler();
AINFO << "Lateral control gain scheduler loaded";
Interpolation1D::DataType xy1, xy2; // 加载标定表
for (const auto &scheduler : lat_err_gain_scheduler.scheduler()) {
xy1.push_back(std::make_pair(scheduler.speed(), scheduler.ratio())); // 横向偏差标定表
}
for (const auto &scheduler : heading_err_gain_scheduler.scheduler()) {
xy2.push_back(std::make_pair(scheduler.speed(), scheduler.ratio())); // 航向偏差标定表
}
lat_err_interpolation_.reset(new Interpolation1D); // 一维线性插值
ACHECK(lat_err_interpolation_->Init(xy1))
<< "Fail to load lateral error gain scheduler";
heading_err_interpolation_.reset(new Interpolation1D);
ACHECK(heading_err_interpolation_->Init(xy2))
<< "Fail to load heading error gain scheduler";
}
2.6 LatController::ComputeControlCommand(横向控制指令)
Status LatController::ComputeControlCommand(
const localization::LocalizationEstimate *localization,
const canbus::Chassis *chassis,
const planning::ADCTrajectory *planning_published_trajectory,
ControlCommand *cmd) {
auto vehicle_state = injector_->vehicle_state();
auto target_tracking_trajectory = *planning_published_trajectory;
// Transform the coordinate of the planning trajectory from the center of the
// rear-axis to the center of mass, if conditions matched
// 低速时使用几何中心
if (((FLAGS_trajectory_transform_to_com_reverse &&
vehicle_state->gear() == canbus::Chassis::GEAR_REVERSE) ||
(FLAGS_trajectory_transform_to_com_drive &&
vehicle_state->gear() == canbus::Chassis::GEAR_DRIVE)) &&
enable_look_ahead_back_control_) {
trajectory_analyzer_.TrajectoryTransformToCOM(lr_);
}
对前进或倒车时中点的选择,倒车时会使用车辆的后轴中心,前进时会使用车辆的几何中心。倒车时主要使用的是车辆的运动学模型。
// Re-build the vehicle dynamic models at reverse driving (in particular,
// replace the lateral translational motion dynamics with the corresponding
// kinematic models)
if (vehicle_state->gear() == canbus::Chassis::GEAR_REVERSE) {
/*
A matrix (Gear Reverse)
[0.0, 0.0, 1.0 * v 0.0;
0.0, (-(c_f + c_r) / m) / v, (c_f + c_r) / m,
(l_r * c_r - l_f * c_f) / m / v;
0.0, 0.0, 0.0, 1.0;
0.0, ((lr * cr - lf * cf) / i_z) / v, (l_f * c_f - l_r * c_r) / i_z,
(-1.0 * (l_f^2 * c_f + l_r^2 * c_r) / i_z) / v;]
*/
cf_ = -control_conf_->lat_controller_conf().cf();
cr_ = -control_conf_->lat_controller_conf().cr();
matrix_a_(0, 1) = 0.0;
matrix_a_coeff_(0, 2) = 1.0;
} else {
对矩阵a的个别项进行修改。
2.7 LatController::UpdateDrivingOrientation()
void LatController::UpdateDrivingOrientation() {
auto vehicle_state = injector_->vehicle_state();
driving_orientation_ = vehicle_state->heading();
matrix_bd_ = matrix_b_ * ts_;
// Reverse the driving direction if the vehicle is in reverse mode
if (FLAGS_reverse_heading_control) {
if (vehicle_state->gear() == canbus::Chassis::GEAR_REVERSE) {
driving_orientation_ =
common::math::NormalizeAngle(driving_orientation_ + M_PI);
// Update Matrix_b for reverse mode
matrix_bd_ = -matrix_b_ * ts_;
ADEBUG << "Matrix_b changed due to gear direction";
}
}
}
对驾驶车辆的运动方向做判断,同时更新控制结果的输出。
// Update state = [Lateral Error, Lateral Error Rate, Heading Error, Heading
// Error Rate, preview lateral error1 , preview lateral error2, ...]
UpdateState(debug);
UpdateMatrix(); //矩阵状态更新
// Compound discrete matrix with road preview model
UpdateMatrixCompound();
对横向偏差、横向偏差变化率、航向偏差、航向偏差变化率进行计算。
2.8 LatController::UpdateState
void LatController::UpdateState(SimpleLateralDebug *debug) {
auto vehicle_state = injector_->vehicle_state();
if (FLAGS_use_navigation_mode) {
ComputeLateralErrors(
0.0, 0.0, driving_orientation_, vehicle_state->linear_velocity(),
vehicle_state->angular_velocity(), vehicle_state->linear_acceleration(),
trajectory_analyzer_, debug);
} else {
// Transform the coordinate of the vehicle states from the center of the
// rear-axis to the center of mass, if conditions matched
const auto &com = vehicle_state->ComputeCOMPosition(lr_);
ComputeLateralErrors(
com.x(), com.y(), driving_orientation_,
vehicle_state->linear_velocity(), vehicle_state->angular_velocity(),
vehicle_state->linear_acceleration(), trajectory_analyzer_, debug);
}
ComputeLateralErrors通过获取当前车辆的位置、车辆的行驶状态(前进还是后退)、车辆的线速度、角速度、线加速度、轨迹等信息来计算横向偏差
2.9 LatController::ComputeLateralErrors
void LatController::ComputeLateralErrors(
const double x, const double y, const double theta, const double linear_v,
const double angular_v, const double linear_a,
const TrajectoryAnalyzer &trajectory_analyzer, SimpleLateralDebug *debug) {
TrajectoryPoint target_point;
if (FLAGS_query_time_nearest_point_only) {
target_point = trajectory_analyzer.QueryNearestPointByAbsoluteTime(
Clock::NowInSeconds() + query_relative_time_);
} else {
if (FLAGS_use_navigation_mode &&
!FLAGS_enable_navigation_mode_position_update) {
target_point = trajectory_analyzer.QueryNearestPointByAbsoluteTime(
Clock::NowInSeconds() + query_relative_time_);
} else {
target_point = trajectory_analyzer.QueryNearestPointByPosition(x, y);
}
}
3. 云平台实践教学
3.1 前置步骤
在终端中输入以下指令,启动dreamview
aem bootstrap start
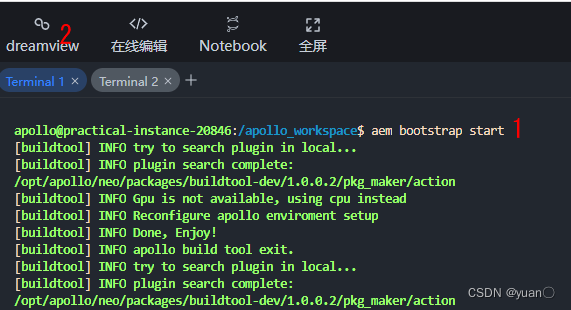
运行成功后,点击左上角dreamview按钮。当网页中出现apollo后, 即表示dreamview启动成功了, 为了便于调试,在该页面上,我们选择车辆(vehicle) 为MKZ,关闭mute,选择地图Apollo Virutal Map。

点击Sim Control
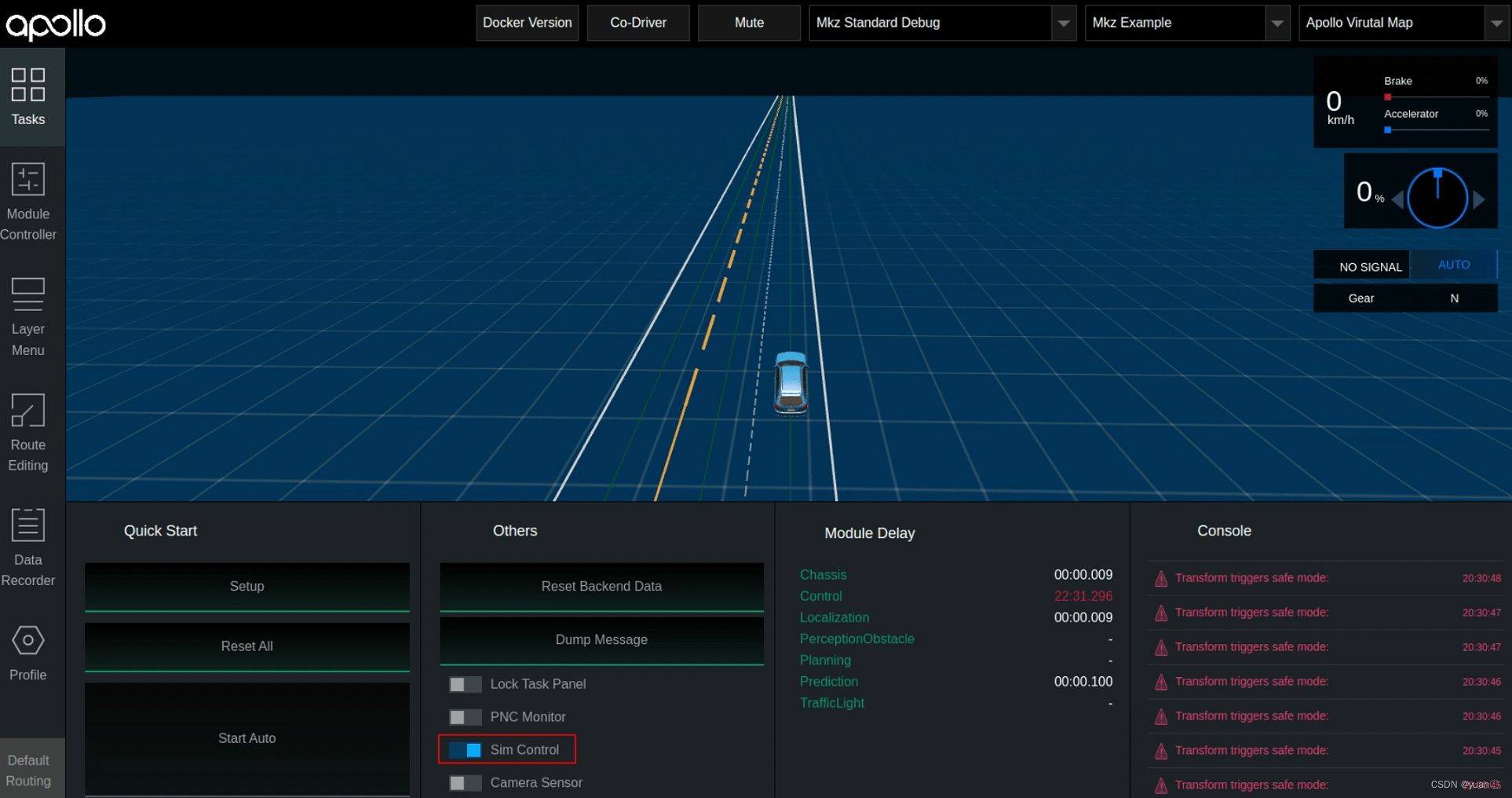
点击Profile, 下载动力学模型,Mkz Model (lincolnmkz动力学模型),Point Mass Model (惯性模型) 。然后选择Dynamic Model,选择Mkz Model.
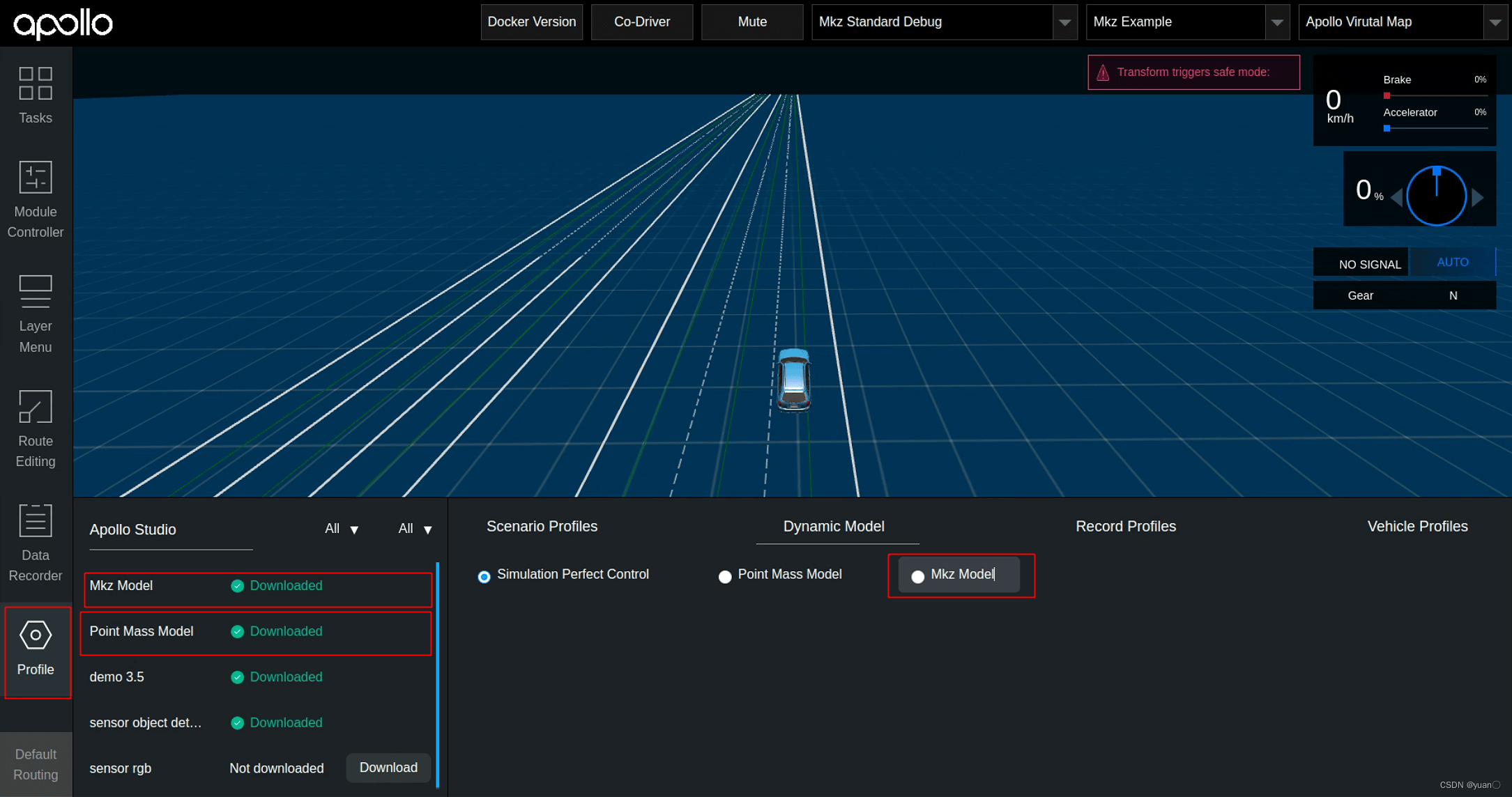
启动Planning, Routing, Control,
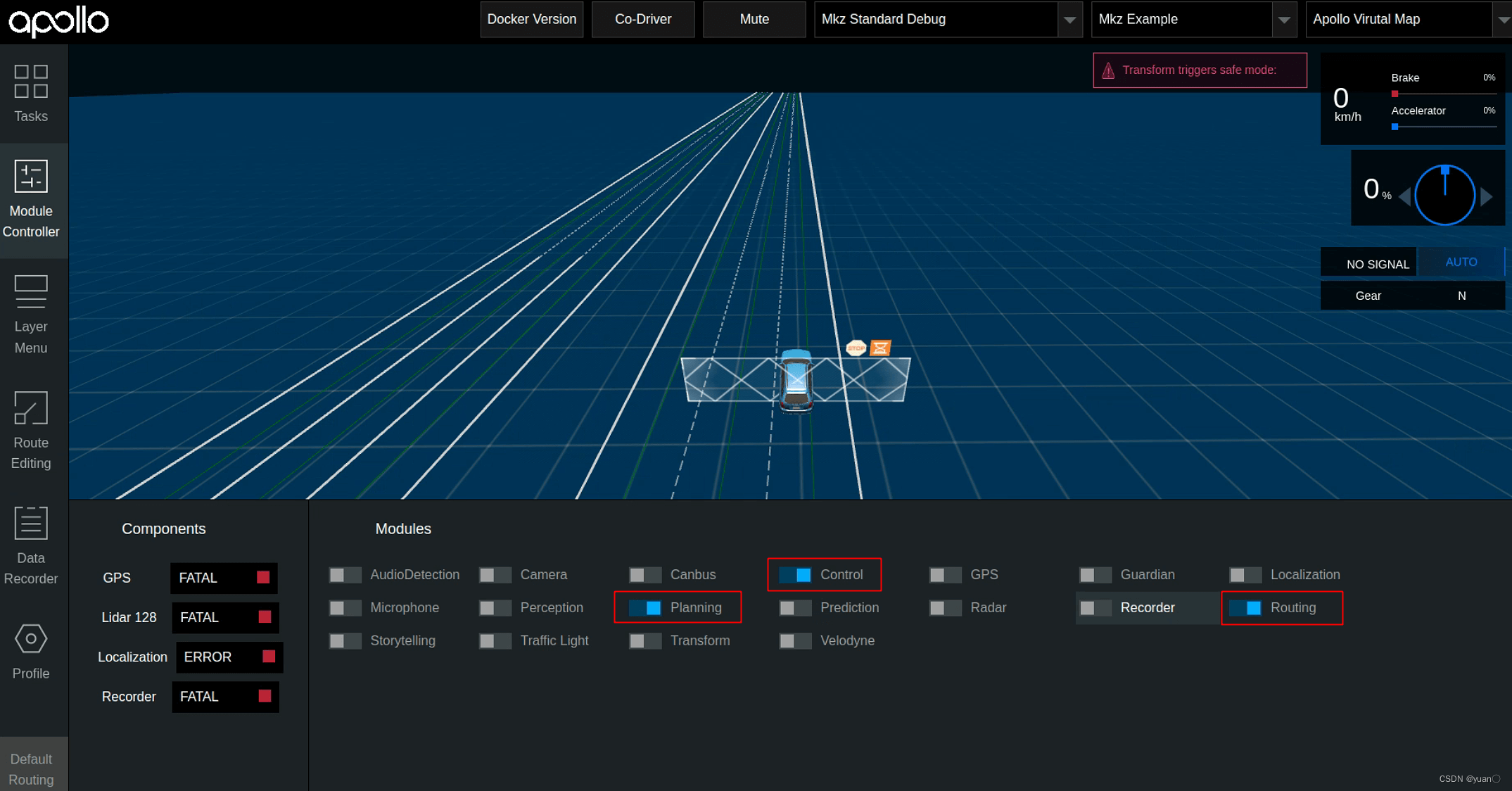
在Route Editing页面,选择起点,终点,选择SendRouting Request。发送前点开recorder
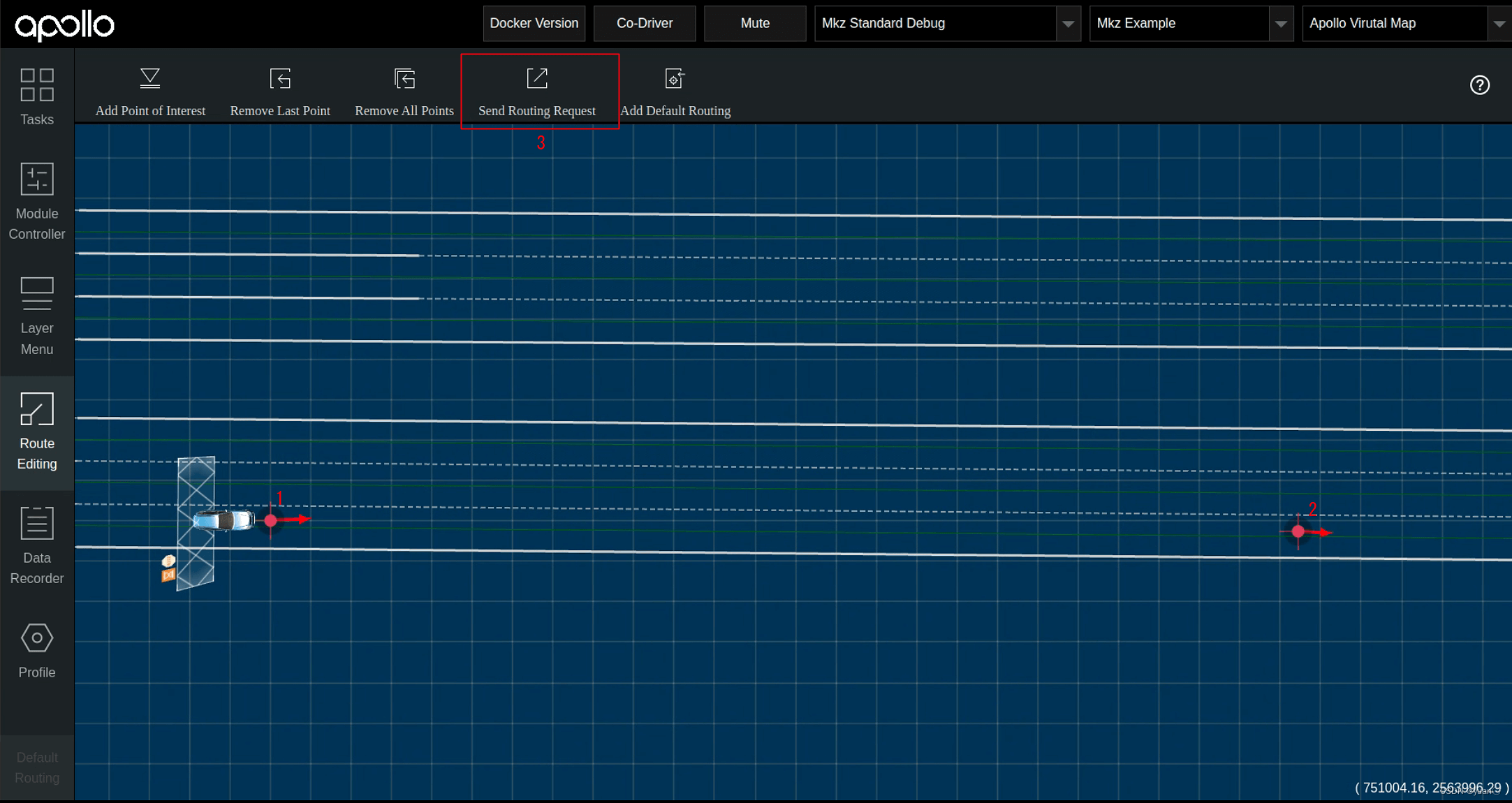
查看车辆前方能够正常生成规划线,此时切换到Tasks页面,点击StartAuto。
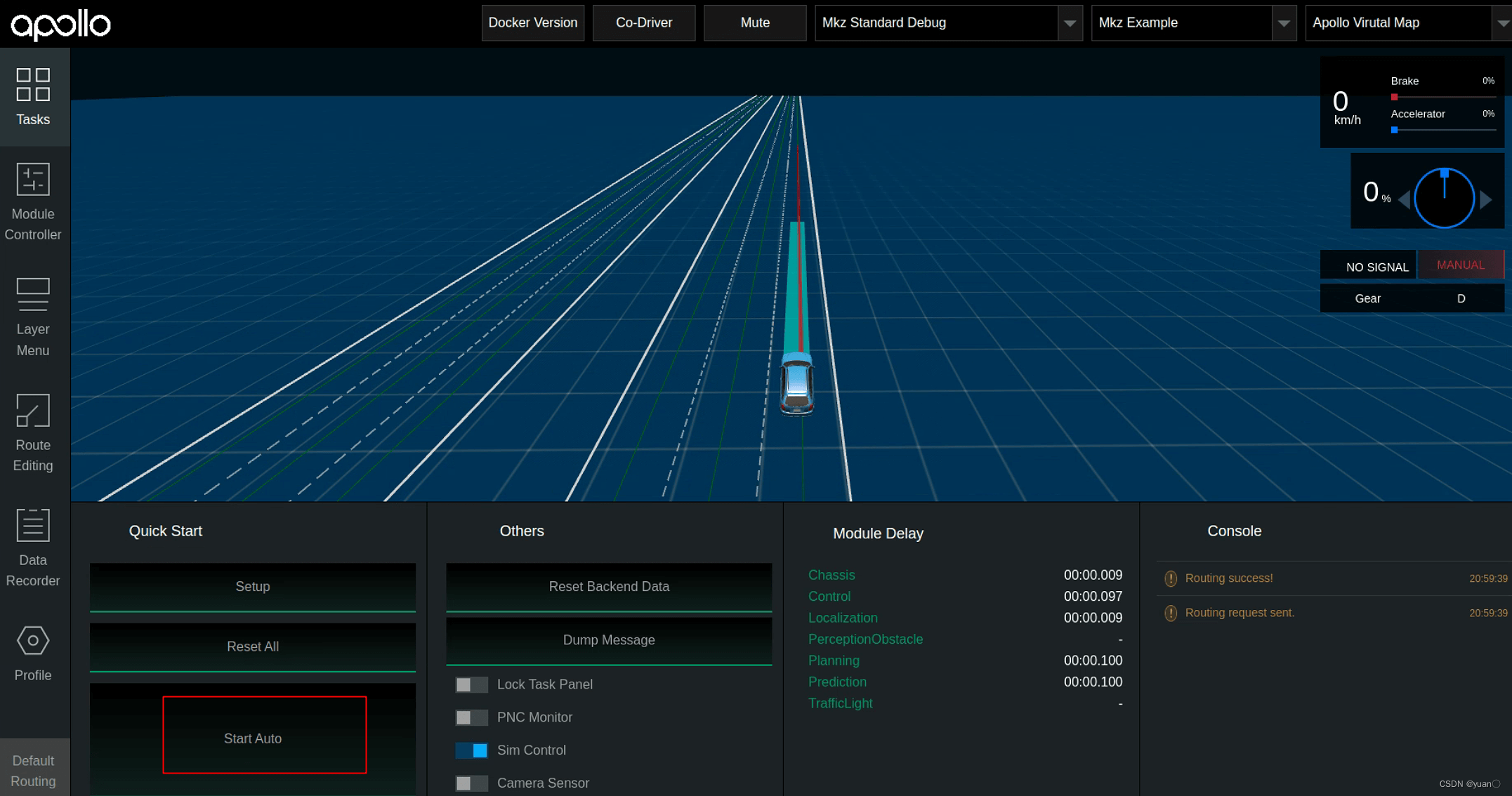
点击Dreamview左侧菜单栏Tasks按钮,关闭LockTask Panel,打开PNC monitor功能按钮,点击右侧Control按钮,可以查看控制相关的数据。
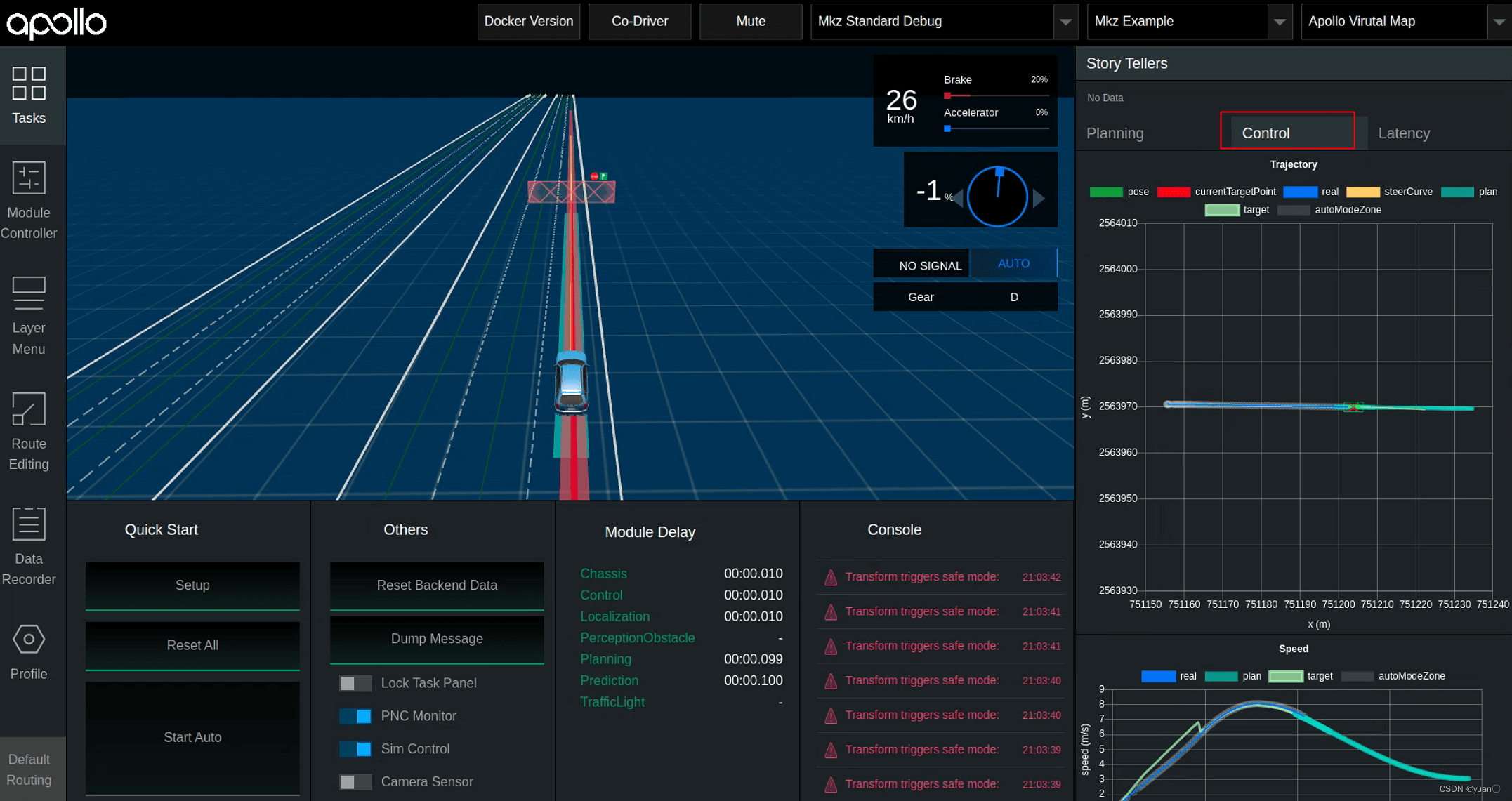
通过下拉右边栏,可查看控制相关参数的变化,比如右侧第二个图表speed,蓝色曲线表示车辆的实际车速,青绿色的表示规划的参考车速,可看到实际车速与规划速度的跟随情况,从而可以进行控制效果。
3.2 控制参数修改
(1)查看纵向控制参数配置
点击在线编辑,打开控制参数配置文
件/apollo_workspace/modules/control/conf/control_conf.pb.txt,可查看apollo默认的控制参数。
找到/apollo/modules/control/conf/control_conf.pb.txt
从配置文件内,可查看横向控制参数如下,横向LQR控制参数主要在lat_controller_conf 内,横向控制参数调节:横向位置误差(q0),横向位置误差变化率(q1),航向误差(q2),航向误差变化率(q3)。
(1)LQR参数
lat_controller_conf {
matrix_q: 0.05
matrix_q: 0.0
matrix_q: 1.0
matrix_q: 0.0
reverse_matrix_q: 0.5
reverse_matrix_q: 0.0
reverse_matrix_q: 0.4
reverse_matrix_q: 0.0
}
(2)横向位置增益,可配置不同速度范围的横向位置调节增益。
lat_err_gain_scheduler {
scheduler {
speed: 4.0
ratio: 1.0
}
scheduler {
speed: 8.0
ratio: 0.6
}
scheduler {
speed: 12.0
ratio: 0.2
}
scheduler {
speed: 20.0
ratio: 0.1
}
scheduler {
speed: 25.0
ratio: 0.05
}
}
(3)横向航向角增益,可配置不同速度范围的航向角调节增益。
heading_err_gain_scheduler {
scheduler {
speed: 4.0
ratio: 1.0
}
scheduler {
speed: 8.0
ratio: 0.6
}
scheduler {
speed: 12.0
ratio: 0.4
}
scheduler {
speed: 20.0
ratio: 0.2
}
scheduler {
speed: 25.0
ratio: 0.1
}
}
(4)实验时,使用默认控制参数,进行转向或直行仿真,根据5.2步骤并点击recorder按钮,进行录制数据包。可以通过PNC monitor或control_info工具,对控制效果进行简单分析。
(5)然后将横向位置误差增益和航向角增益系数ratio修改为0,查看转弯画龙效果。
lat_err_gain_scheduler {
scheduler {
speed: 4.0
ratio: 0.0
}
scheduler {
speed: 8.0
ratio: 0.0
}
scheduler {
speed: 12.0
ratio: 0.0
}
scheduler {
speed: 20.0
ratio: 0.0
}
scheduler {
speed: 25.0
ratio: 0.0
}
}
heading_err_gain_scheduler {
scheduler {
speed: 4.0
ratio: 0.0
}
scheduler {
speed: 8.0
ratio: 0.0
}
scheduler {
speed: 12.0
ratio: 0.0
}
scheduler {
speed: 20.0
ratio: 0.0
}
scheduler {
speed: 25.0
ratio: 0.0
}
}
打卡notebook,用内置脚本绘图并分析数据。
%matplotlib notebook
run control_info/control_info.py --path /apollo/data/bag/2023-01-19-03-19-59_s/
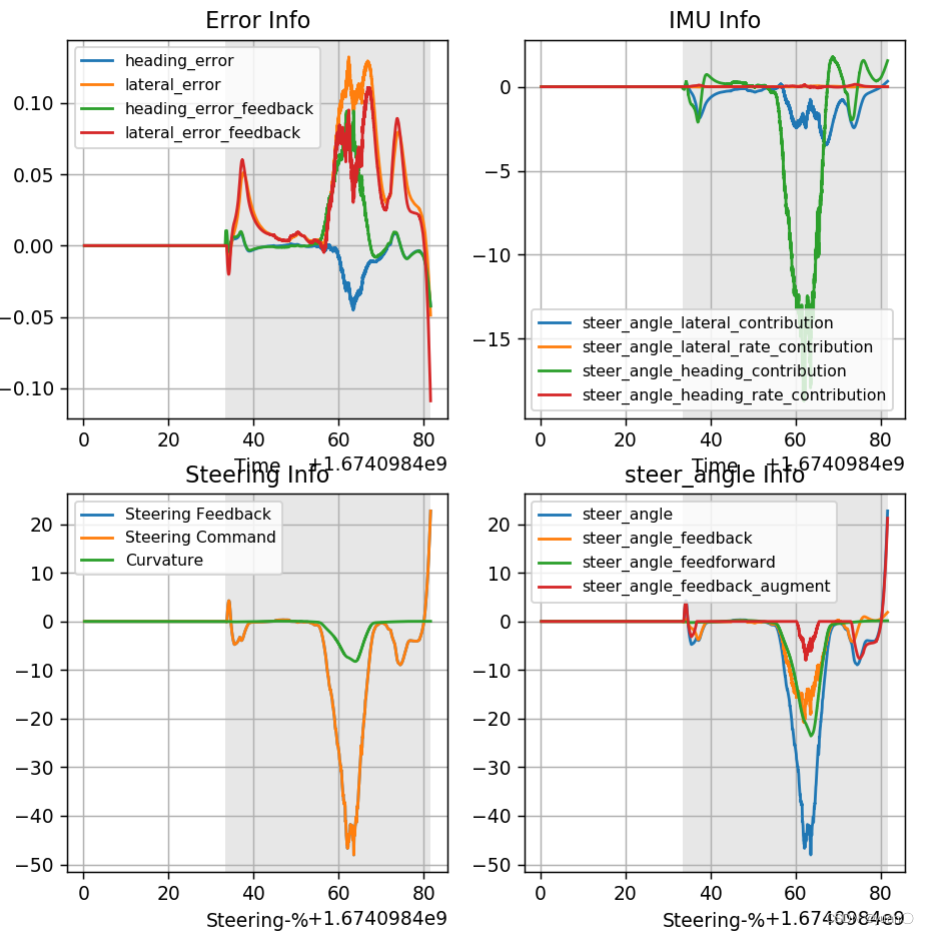
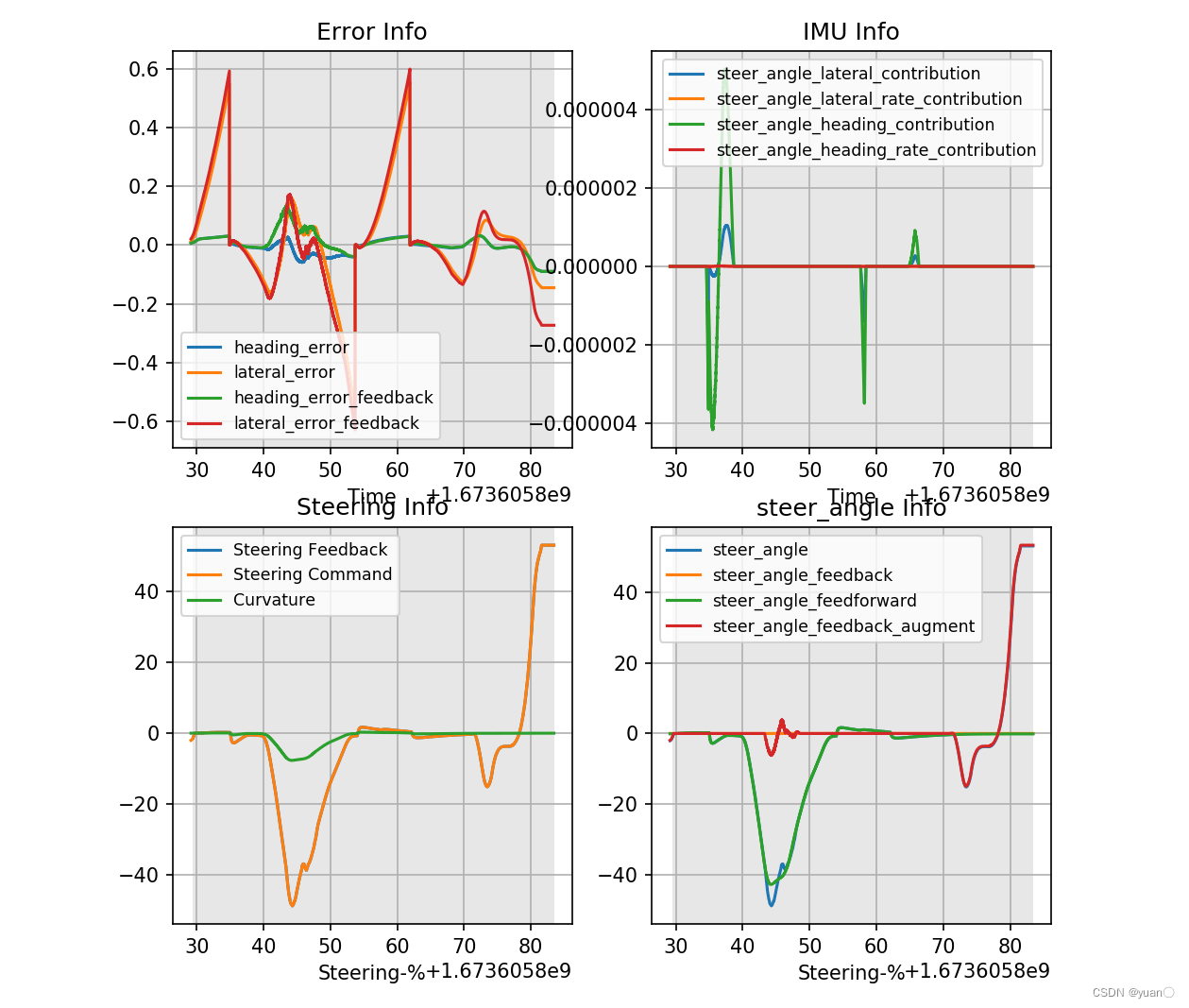
lateral_error最大值达到0.6左右,横摆偏差较大最后
以上就是重要芹菜最近收集整理的关于Apollo星火计划学习笔记——Control 专项讲解(LQR)前言1. 算法相关基础2. LQR代码解析3. 云平台实践教学的全部内容,更多相关Apollo星火计划学习笔记——Control内容请搜索靠谱客的其他文章。








发表评论 取消回复