文章目录
- 详细步骤
- 加密算法
- 对秘钥的处理
- 对明文的处理
- f函数
- 解密算法
- 代码实现
- 源代码
- 运行结果
详细步骤
（为了方便程序debug的时候对每一步进行检查，因此本文将会对算法中每一步都给出详细的结果，输出位置也在代码中以注释的方式给出，请放心食用）加密过程使用下面这个例子：
明文：P = 0123456789ABCDEF
密钥：K = 133457799BBCDFF1
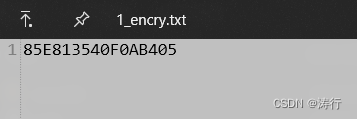
密文：C = 85E813540F0AB405
加密算法
对秘钥的处理
将密钥K转换为二进制
复制代码
1
2K = 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001
将K进行PC-1变换，PC-1表格为：
复制代码
1
2
3
4
5
6
7
8
9
10
11PC-1 57 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 27 19 11 3 60 52 44 36 63 55 47 39 31 23 15 7 62 54 46 38 30 22 14 6 61 53 45 37 29 21 13 5 28 20 12 4
具体方法为：由于表格中的第一位为57，所以将新密钥的第一位换为旧密钥的第57位，同理，第二位为旧密钥的第49位，以此类推，由于PC-1表格中只有48位数据，因此变换过之后会丢弃8位，得到的新密钥为：
复制代码
1
2K = 1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111
将新密钥按28位一组拆分为C0和D0两部分
复制代码
1
2
3C0 = 1111000 0110011 0010101 0101111 D0 = 0101010 1011001 1001111 0001111
创建与C0和D0相同长度的16组Cn、Dn，对于每一组Ci、Di，都是由Ci-1、Di-1左移得到的，每次左移的位数由以下数组确定
复制代码
1
2MOVE[16] = {1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1};
如果移位数位1，则将C(D)i-1除第一位之外的所有为左移一位，最后一位等于第一位，一位次数为2则向前移动两位，最后两位等于C(D)i-1前两位，对于例子中的明文，其经过处理之后的C和D见下表所示
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18C0 = 1111000011001100101010101111 D0 = 0101010101100110011110001111 C1 = 1110000110011001010101011111 D1 = 1010101011001100111100011110 C2 = 1100001100110010101010111111 D2 = 0101010110011001111000111101 C3 = 0000110011001010101011111111 D3 = 0101011001100111100011110101 C4 = 0011001100101010101111111100 D4 = 0101100110011110001111010101 C5 = 1100110010101010111111110000 D5 = 0110011001111000111101010101 C6 = 0011001010101011111111000011 D6 = 1001100111100011110101010101 C7 = 1100101010101111111100001100 D7 = 0110011110001111010101010110 C8 = 0010101010111111110000110011 D8 = 1001111000111101010101011001 C9 = 0101010101111111100001100110 D9 = 0011110001111010101010110011 C10 = 0101010111111110000110011001 D10 = 1111000111101010101011001100 C11 = 0101011111111000011001100101 D11 = 1100011110101010101100110011 C12 = 0101111111100001100110010101 D12 = 0001111010101010110011001111 C13 = 0111111110000110011001010101 D13 = 0111101010101011001100111100 C14 = 1111111000011001100101010101 D14 = 1110101010101100110011110001 C15 = 1111100001100110010101010111 D15 = 1010101010110011001111000111 C16 = 1111000011001100101010101111 D16 = 0101010101100110011110001111
将每对CD从n=1到n=16按照CnDn的方式拼接，并经过PC-2表格变换之后形成密钥Kn，PC-2表格如下
复制代码
1
2
3
4
5
6
7
8
9
10
11PC-2 14 17 11 24 1 5 3 28 15 6 21 10 23 19 12 4 26 8 16 7 27 20 13 2 41 52 31 37 47 55 30 40 51 45 33 48 44 49 39 56 34 53 46 42 50 36 29 32
最终形成的秘钥K1到K16为
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17K1 = 000110 110000 001011 101111 111111 000111 000001 110010 K2 = 011110 011010 111011 011001 110110 111100 100111 100101 K3 = 010101 011111 110010 001010 010000 101100 111110 011001 K4 = 011100 101010 110111 010110 110110 110011 010100 011101 K5 = 011111 001110 110000 000111 111010 110101 001110 101000 K6 = 011000 111010 010100 111110 010100 000111 101100 101111 K7 = 111011 001000 010010 110111 111101 100001 100010 111100 K8 = 111101 111000 101000 111010 110000 010011 101111 111011 K9 = 111000 001101 101111 101011 111011 011110 011110 000001 K10 = 101100 011111 001101 000111 101110 100100 011001 001111 K11 = 001000 010101 111111 010011 110111 101101 001110 000110 K12 = 011101 010111 000111 110101 100101 000110 011111 101001 K13 = 100101 111100 010111 010001 111110 101011 101001 000001 K14 = 010111 110100 001110 110111 111100 101110 011100 111010 K15 = 101111 111001 000110 001101 001111 010011 111100 001010 K16 = 110010 110011 110110 001011 000011 100001 011111 110101
密钥处理的流程图：
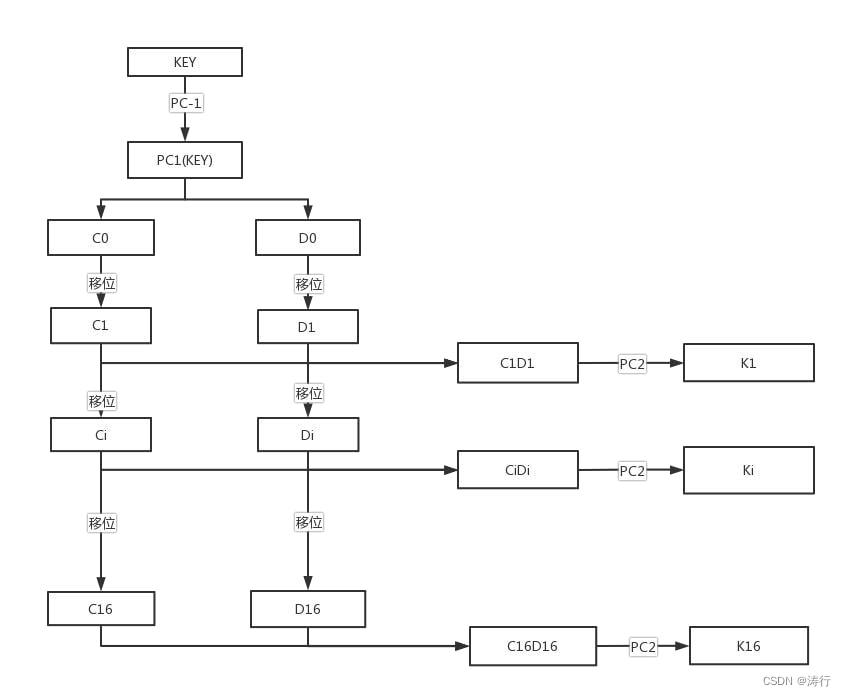
对明文的处理
将16位明文M转化为64位2进制，并按照32位一组分成L(left)和R(right)两部分
复制代码
1
2
3
4M = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 L = 0000 0001 0010 0011 0100 0101 0110 0111 R = 1000 1001 1010 1011 1100 1101 1110 1111
对明文M进行IP（Initial permutation）表格变换，具体方式与PC变换一样，之后形成的数据为：
复制代码
1
2IP = 1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1010 1111 0000 1010 1010
将64位的IP按照32位一组分成左半边的L0和右半边的R0，对于例子，我们得到
复制代码
1
2
3L0 = 1100 1100 0000 0000 1100 1100 1111 1111 R0 = 1111 0000 1010 1010 1111 0000 1010 1010
接着进行16轮Feistel循环，对1≤n≤16，使用一个函数f。函数f输入两个区块——一个32位的数据区块和一个48位的秘钥区块Kn ——输出一个32位的区块。让n从1循环到16，计算
Ln = Rn-1
Rn = Ln-1 ⊕ f(Rn-1, Kn)
流程图如下
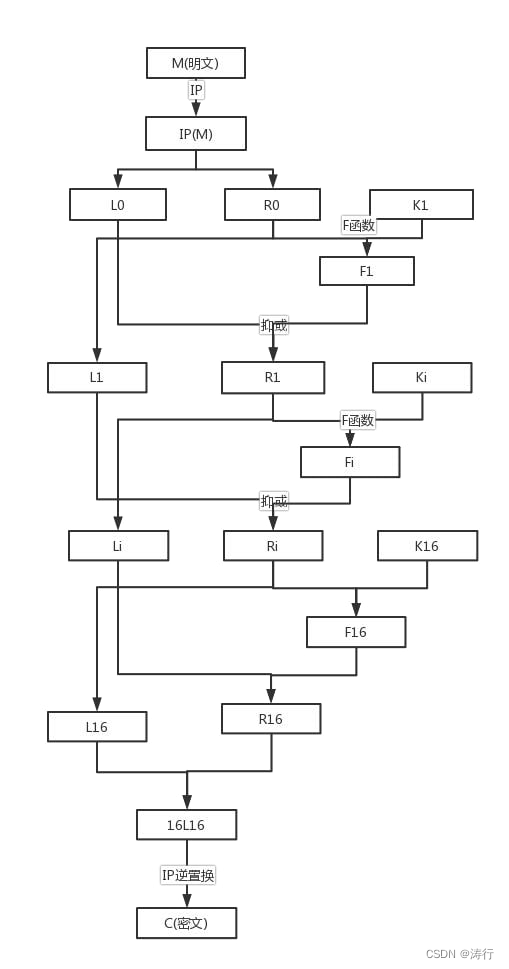
下面针对f函数进行详细说明
f函数
对f函数，输入的R为32位，而K是48位，因此需要对R进行扩展，具体方法为通过E表格的变换
复制代码
1
2
3
4
5
6
7
8
9
10
11E表 32 1 2 3 4 5 4 5 6 7 8 9 8 9 10 11 12 13 12 13 14 15 16 17 16 17 18 19 20 21 20 21 22 23 24 25 24 25 26 27 28 29 28 29 30 31 32 1
E( R)的第一位来自R的第32位，E( R)的第2位来自R的第1位，以此类推，对例子中的R，给出所有扩展后的结果如下：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17E(R1): 011110100001010101010101011110100001010101010101 E(R2): 011101011110101001010100001100001010101000001001 E(R3): 111001011000000000000010101110101110100001010011 E(R4): 010100000100001011111000000001010111111110101001 E(R5): 101110101110100100000100000000000000001000001010 E(R6): 110001010100001001011111110100001100000110101111 E(R7): 111101010010101100001111111001011010101101010011 E(R8): 000000001100001001010101010111110100000010100000 E(R9): 011010101010101101010010101001010111110010100001 E(R10): 000100001000001111111001011000001100001111110100 E(R11): 010110101111111010101011111010101111110110100101 E(R12): 011000001010101111110000000111111000001111110001 E(R13): 001110101011110111111010100011110000001011110000 E(R14): 000011110001011000000110100010101010101011110100 E(R15): 111000000101010001011001010010101100000001011011 E(R16): 001000000110101000000100000110100100000110101000
得到E( R)之后，与K按位异或得到Kn ⊕ E(Rn-1)，下表为每次抑或之后得到的结果
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17E(R1) XOR K1 = 011000010001011110111010100001100110010100100111 E(R2) XOR K2 = 000011000100010010001101111010110110001111101100 E(R3) XOR K3 = 101100000111110010001000111110000010011111001010 E(R4) XOR K4 = 001000101110111100101110110111100100101010110100 E(R5) XOR K5 = 110001100000010100000011111010110101000110100010 E(R6) XOR K6 = 101001101110011101100001100000001011101010000000 E(R7) XOR K7 = 000110011010111110111000000100111011001111101111 E(R8) XOR K8 = 111101110100100001101111100111100111101101011011 E(R9) XOR K9 = 100010100111000010111001010010001001101100100000 E(R10)XOR K10 = 101000010111000010111110110110101000010110111011 E(R11)XOR K11 = 011110111010000101111000001101000010111000100011 E(R12)XOR K12 = 000101011101101000000101100010111110010000011000 E(R13)XOR K13 = 101011010111100000101011011101011011100010110001 E(R14)XOR K14 = 010100000101010110110001011110000100110111001110 E(R15)XOR K15 = 010111111100010111010100011101111111111101010001 E(R16)XOR K16 = 111010110101011110001111000101000101011001011101
抑或后的结果将经过S盒处理，首先给出8个S盒（对于每个S盒，行号和列号都从0开始计算）：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51S-Box S1 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13 S2 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9 S3 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12 S4 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15 13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14 S5 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3 S6 12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13 S7 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12 S8 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11
具体步骤如下：将每轮迭代得到的E(R ) ⊕+ K 的48位按每6位一组分成8组，得到8组6位2进制数据，对于每一组6位2进制数据（以011001为例）做如下处理：取第一位和最后以为二进制数据合并构成一个新的二进制数（01）作为行号（1），二三四五位构成一个新的二进制数（1000）作为列号（8），用行号和列号去寻找S盒中对应的数字（10），形成新的二进制数（1010）作为压缩后的新数。每一轮迭代后得到的E(R ) ⊕ K分成8组后按顺序分别经过8个S盒压缩，得到的新的32位的二进制数即为经过S盒压缩的结果。对例子中的数进行S盒压缩得到的结果为：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17S1: 01011100100000101011010110010111 S2: 11111000110100000011101010101110 S3: 00100111000100001110000101101111 S4: 00100001111011011001111100111010 S5: 01010000110010000011000111101011 S6: 01000001111100110100110000111101 S7: 00010000011101010100000010101101 S8: 01101100000110000111110010101110 S9: 00010001000011000101011101110111 S10:11011010000001000101001001110101 S11:01110011000001011101000100000001 S12:01111011100010110010011000110101 S13:10011010110100011000101101001111 S14:01100100011110011001101011110001 S15:10110010111010001000110100111100 S16:10100111100000110010010000101001
对于每个32位的S盒输出的结果，再进行一次P变换就是f函数最终的结果了，P表如下：
复制代码
1
2
3
4
5
6
7
8
9
10
11P 16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10 2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25
具体操作步骤与IP和E表类似，最终生成的16个f函数的结果为：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17F[1]: 00100011010010101010100110111011 F[2]: 00111100101010111000011110100011 F[3]: 01001101000101100110111010110000 F[4]: 10111011001000110111011101001100 F[5]: 00101000000100111010110111000011 F[6]: 10011110010001011100110100101100 F[7]: 10001100000001010001110000100111 F[8]: 00111100000011101000011011111001 F[9]: 00100010001101100111110001101010 F[10]: 01100010101111001001110000100010 F[11]: 11100001000001001111101000000010 F[12]: 11000010011010001100111111101010 F[13]: 11011101101110110010100100100010 F[14]: 10110111001100011000111001010101 F[15]: 01011011100000010010011101101110 F[16]: 11001000110000000100111110011000
f函数的流程图如下：
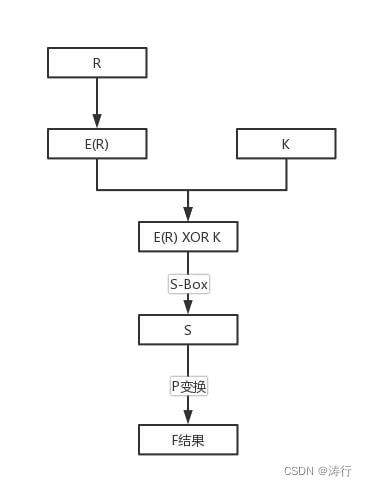
f函数之后，回到Feistel循环，继续L和F的按位异或，每一步得出的Rn和Ln为：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17L[1]: 11110000101010101111000010101010 R[1]: 11101111010010100110010101000100 L[2]: 11101111010010100110010101000100 R[2] : 11001100000000010111011100001001 L[3]: 11001100000000010111011100001001 R[3]: 10100010010111000000101111110100 L[4]: 10100010010111000000101111110100 R[4]: 01110111001000100000000001000101 L[5]: 01110111001000100000000001000101 R[5]: 10001010010011111010011000110111 L[6]: 10001010010011111010011000110111 R[6]: 11101001011001111100110101101001 L[7]: 11101001011001111100110101101001 R[7]: 00000110010010101011101000010000 L[8]: 00000110010010101011101000010000 R[8]: 11010101011010010100101110010000 L[9]: 11010101011010010100101110010000 R[9]: 00100100011111001100011001111010 L[10]: 00100100011111001100011001111010 R[10]: 10110111110101011101011110110010 L[11]: 10110111110101011101011110110010 R[11]: 11000101011110000011110001111000 L[12]: 11000101011110000011110001111000 R[12]: 01110101101111010001100001011000 L[13]: 01110101101111010001100001011000 R[13]: 00011000110000110001010101011010 L[14]: 00011000110000110001010101011010 R[14]: 11000010100011001001011000001101 L[15]: 11000010100011001001011000001101 R[15]: 01000011010000100011001000110100 L[16]: 01000011010000100011001000110100 R[16]: 00001010010011001101100110010101
对最终生成的L16和R16，按照R16L16的方式将其拼接成64位的新二进制数，然后对其执行IP逆置换，IP逆置换表如下所示：
复制代码
1
2
3
4
5
6
7
8
9
10
11IP-1 40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31 38 6 46 14 54 22 62 30 37 5 45 13 53 21 61 29 36 4 44 12 52 20 60 28 35 3 43 11 51 19 59 27 34 2 42 10 50 18 58 26 33 1 41 9 49 17 57 25
R16L16与最终结果为：
复制代码
1
2
3R16L16 = 00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100 IP-1 = 10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101
将IP-1转换为16进制为：85E813540F0AB405，这就是加密之后的密文
解密算法
解密过程与加密完全相同，只是在1f函数中过程中，将子秘钥1-16反过来使用就行（例如E(R1) XOR K16, E(R2) XOR K15，以此类推），具体可以比较代码中encrypt和decrypt函数，除了K之外完全相同（甚至可以写成一个函数，加解密做一个判断）
代码实现
源代码
使用C++语言实现本算法：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439/******************************************* * Name: myDES.cpp * Author: kongtaoxing ******************************************/ #include<iostream> #include<string> #include<fstream> #include<vector> #include<algorithm> using namespace std; // 以下为算法所需要的表格 // 为了适应C++语言，表格中的所有数字都做了减1处理，以使第一位为0 // IP置换表 int IP[64] = { 57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3, 61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7, 56, 48, 40, 32, 24, 16, 8, 0, 58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4, 62, 54, 46, 38, 30, 22, 14, 6 }; // IP逆置换表 int IPni[64] = { 39, 7, 47, 15, 55, 23, 63, 31, 38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29, 36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27, 34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25, 32, 0, 40, 8, 48, 16, 56, 24 }; //S盒 int S[8][4][16] = { //S1 { {14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7}, { 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8}, { 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0}, {15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13} }, //S2 { {15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10}, {3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5}, {0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15}, {13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9} }, //S3 { {10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8}, {13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1}, {13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7}, {1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12} }, //S4 { {7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15}, {13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9}, {10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4}, {3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14} }, //S5 { {2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9}, {14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6}, {4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14}, {11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3} }, //S6 { {12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11}, {10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8}, {9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6}, {4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13} }, //S7 { {4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1}, {13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6}, {1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2}, {6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12} }, //S8 { {13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7}, {1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2}, {7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8}, {2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11} } }; //扩充置换表E，用于把R从32位扩展到48位 int E[48] = { 31, 0, 1, 2, 3, 4, 3, 4, 5, 6, 7, 8, 7, 8, 9, 10, 11, 12, 11, 12, 13, 14, 15, 16, 15, 16, 17, 18, 19, 20, 19, 20, 21, 22, 23, 24, 23, 24, 25, 26, 27, 28, 27, 28, 29, 30, 31, 0 }; //置换函数P int P[32] = { 15, 6, 19, 20, 28, 11, 27, 16, 0, 14, 22, 25, 4, 17, 30, 9, 1, 7, 23, 13, 31, 26, 2, 8, 18, 12, 29, 5, 21, 10, 3, 24 }; //PC1，用以置换密钥 int PC1[56] = { 56, 48, 40, 32, 24, 16, 8, 0, 57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18, 10, 2, 59, 51, 43, 35, 62, 54, 46, 38, 30, 22, 14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 60, 52, 44, 36, 28, 20, 12, 4, 27, 19, 11, 3 }; //PC2，移位之后置换密钥 int PC2[56] = { 13, 16, 10, 23, 0, 4, 2, 27, 14, 5, 20, 9, 22, 18, 11, 3, 25, 7, 15, 6, 26, 19, 12, 1, 40, 51, 30, 36, 46, 54, 29, 39, 50, 44, 32, 47, 43, 48, 38, 55, 33, 52, 45, 41, 49, 35, 28, 31 }; //左移次数，用以移动密钥 int MOVE[16] = { 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1 }; // 算法主体 string encrypt(string p, string k); //加密函数主函数 string decrypt(string c, string k); //解密函数 string LowToUpper(string low); //小写字母转大写字母 string HextoBin(string Hex); //十六进制转二进制 string BintoHex(string Bin); //二进制转十六进制 vector<string> subKey(string k); //子秘钥生成函数 string feistel(string R, string K); //F函数, 不是feistel，起错名了..... int main() { string PATH_P, PATH_C, PATH_K = ""; string p, c, k; cout << "请输入你想加密还是解密，加密为e，解密为d："; string ed; cin >> ed; cout << "n请输入需要加解密的文件路径(路径中的单斜杠请输入为双斜杠，以下同)："; cin >> PATH_P; ifstream pFile(PATH_P, ios::in); ifstream kFile; if(!pFile.is_open()){ cout << "n打开明文/密文文件失败！" << endl; system("pause"); return 0; } getline(pFile, p); //读入明文/密文字符串 if(p.length() % 16 != 0) { int temp = 16 - p.length() % 16; // cout << 16 - p.length() % 16 << endl; for(int i = 0; i < temp; i++) { p += "0"; //不够加密的话填0补位，方便加密 // cout << i << endl; } } // cout << "补0后的P：" << p << endl; pFile.close(); //及时关闭文件，防止内存泄露 cout << "n请选择准备输入密钥还是选择密钥文件，输入0选择输入密钥， 输入1选择输入密钥文件："; int miyao; cin >> miyao; if(miyao == 0) { cout << "n请输入密钥："; cin >> k; } else { cout << "n请输入密钥文件路径："; cin >> PATH_K; kFile.open(PATH_K, ios::in); if(!kFile.is_open()) { cout << "n打开密钥文件失败！" << endl; system("pause"); return 0; } getline(kFile, k); //读入密钥字符串 kFile.close(); if(k.length() != 16) { cout << "n请将密钥长度限制为16位！" << endl; system("pause"); return 0; } } if(ed == "e") { c = encrypt(p, k); ofstream cFile("1_encry.txt",ios::out); if(!cFile.is_open()) { cout << "创建/打开1_encry.txt失败，请检查文件是否被占用！" << endl; system("pause"); return 0; } cFile << c; cFile.close(); cout << "n密文已保存至程序目录下的1_encry.txt" << endl; } else if(ed == "d") { c = decrypt(p, k); ofstream cFile("1_decry.txt",ios::out); if(!cFile.is_open()) { cout << "创建/打开1_decry.txt失败，请检查文件是否被占用！" << endl; system("pause"); return 0; } cFile << c; cFile.close(); cout << "n明文已保存至程序目录下的1_decry.txt" << endl; } else { cout << "参数错误！" << endl; system("pause"); return 0; } // vector<string> K = subKey(k); // for(int i = 0; i < 16; i++) { // cout << K[i] << endl; // } system("pause"); return 0; } string encrypt(string p, string k){ //加密函数 string pBin = HextoBin(p); vector<string> Key = subKey(k); // for(int i = 0; i < 16; i++) { // cout << "K[" << i << "]: " <<Key[i] << endl; // } string ans = ""; for(int i = 0; i < pBin.length() / 64; i++) { //采用ECB方式 string _P = pBin.substr(i * 64, 64); string pIP(64, '0'); //经IP变换之后的字符串 for(int j = 0; j < 64; j++) { pIP[j] = _P[IP[j]]; } vector<string> L(17, "00000000000000000000000000000000"); vector<string> R(17, "00000000000000000000000000000000"); L[0] = pIP.substr(0, 32); R[0] = pIP.substr(32, 32); // cout << "L[0]: " << L[0] << " R[0]: " << R[0] <<endl; for(int j = 1; j <= 16; j++) { L[j] = R[j - 1]; string F = feistel(R[j - 1], Key[j - 1]); // cout << "F: " << F << endl; for(int k = 0; k < 32; k++){ R[j][k] = (L[j - 1][k] - '0') ^ (F[k] - '0') + '0'; //这几行才是feistel???? } // cout << "L[" << j << "]: " << L[j] << " R[" << j << "]: " << R[j] << endl; } string chaIPni = R[16] + L[16], enc(64, '0'); // cout << chaIPni << endl; for(int j = 0; j < 64; j++) { //IP逆置换 enc[j] = chaIPni[IPni[j]]; } ans += BintoHex(enc); } return ans; } string decrypt(string c, string k) { //解密函数 string cBin = HextoBin(c); vector<string> Key = subKey(k); reverse(Key.begin(), Key.end()); // for(int i = 0; i < 16; i++) { // cout << "Revered Key[" << i << "]: " << Key[i] << endl; // cout << "K: " << Key[i] << endl; // } string ans = ""; for(int i = 0; i < cBin.length() / 64; i++) { // 采用ECB模式解码 string _C = cBin.substr(i * 64, 64); string cIP(64, '0'); // IP置换后的字符串 for(int j = 0; j < 64; j++) { cIP[j] = _C[IP[j]]; } // cout << "P: " << c << endl; // cout << "M: " << _C << endl; vector<string> L(17, "00000000000000000000000000000000"); vector<string> R(17, "00000000000000000000000000000000"); L[0] = cIP.substr(0, 32); R[0] = cIP.substr(32, 32); // cout << "L: " << L[0] << " R: " << R[0] << endl; for(int j = 1; j <= 16; j++) { L[j] = R[j - 1]; string F = feistel(R[j - 1], Key[j - 1]); // cout << "F: " << F << endl; for(int k = 0; k < 32; k++) { R[j][k] = (L[j - 1][k] - '0') ^ (F[k] - '0') + '0'; } // cout << "L: " << L[j] << " R: " << R[j] << endl; } string chaIPni = R[16] + L[16], enc(64, '0'); for(int j = 0; j < 64; j++) { enc[j] = chaIPni[IPni[j]]; // IP逆置换 } ans += BintoHex(enc); } return ans; } string LowToUpper(string low) { for(int i = 0; i < low.length(); i++) { if(low[i] >= 'a' && low[i] <= 'z') { low[i] -= 32; } } return low; } string HextoBin(string Hex) { string Bin = ""; for(int i = 0; i < Hex.length(); i++) { if(Hex[i] == '0') Bin += "0000"; else if(Hex[i] == '1') Bin += "0001"; else if(Hex[i] == '2') Bin += "0010"; else if(Hex[i] == '3') Bin += "0011"; else if(Hex[i] == '4') Bin += "0100"; else if(Hex[i] == '5') Bin += "0101"; else if(Hex[i] == '6') Bin += "0110"; else if(Hex[i] == '7') Bin += "0111"; else if(Hex[i] == '8') Bin += "1000"; else if(Hex[i] == '9') Bin += "1001"; else if(Hex[i] == 'A') Bin += "1010"; else if(Hex[i] == 'B') Bin += "1011"; else if(Hex[i] == 'C') Bin += "1100"; else if(Hex[i] == 'D') Bin += "1101"; else if(Hex[i] == 'E') Bin += "1110"; else Bin += "1111"; } return Bin; } string BintoHex(string Bin) { string Hex = ""; for(int i = 0; i < Bin.length() / 4; i++) { int num = (Bin[4 * i] - '0') * 8 + (Bin[4 * i + 1] - '0') * 4 + (Bin[4 * i + 2] - '0') * 2 + (Bin[4 * i + 3] - '0'); if(0 <= num && num <= 9) Hex += (num + '0'); else if(num == 10) Hex += "A"; else if(num == 11) Hex += "B"; else if(num == 12) Hex += "C"; else if(num == 13) Hex += "D"; else if(num == 14) Hex += "E"; else Hex += "F"; } return Hex; } vector<string> subKey(string k) { string kBin = HextoBin(k); string kBin1(56, '0'); vector<string> C(16, "0000000000000000000000000000"); vector<string> D(16, "0000000000000000000000000000"); vector<string> K(16, "000000000000000000000000000000000000000000000000"); vector<string> K1(16, "000000000000000000000000000000000000000000000000"); for(int i = 0; i < 56; i++) { kBin1[i] = kBin[PC1[i]]; //经过PC1置换丢弃8位 } string C0 = kBin1.substr(0,28); string D0 = kBin1.substr(28,28); for(int i = 0; i < 27; i++) { C[0][i] = C0[i + 1]; D[0][i] = D0[i + 1]; } C[0][27] = C0[0]; D[0][27] = D0[0]; K[0] = C[0] + D[0]; for(int i = 1; i < 16; i++) { //计算16轮密钥 string tempC = C[i - 1].substr(0, MOVE[i]); string tempD = D[i - 1].substr(0, MOVE[i]); for(int j = 0; j < 28 - MOVE[i]; j++) { C[i][j] = C[i - 1][j + MOVE[i]]; D[i][j] = D[i - 1][j + MOVE[i]]; } for(int j = 0; j < MOVE[i]; j++) { C[i][28 - MOVE[i] + j] = tempC[j]; D[i][28 - MOVE[i] + j] = tempD[j]; } K[i] = C[i] + D[i]; } for(int i = 0; i< 16;i++){ for(int j = 0; j < 48; j++){ //经过PC2丢弃8位 K1[i][j] = K[i][PC2[j]]; } } return K1; } string feistel(string R, string K) { //F函数，不是Feistel，起错名了.....Feistel在加密函数里 string _E(48, '0'); //扩展后的R string F(48, '0'); string ret = ""; // cout << "(E)K: " << K << endl; for(int i = 0; i < 48; i++) { _E[i] = R[E[i]]; F[i] = (_E[i] - '0') ^ (K[i] - '0') + '0'; } // cout << "E(R): " << _E << endl; // cout << "E(R) XOR K = " << F <<endl; for(int i = 0; i < 8; i++) { // 经过S盒变换 int x = (F[i * 6] - '0') * 2 + (F[i * 6 + 5] - '0'); int y = (F[i * 6 + 1] -'0') * 8 + (F[i * 6 + 2] - '0') * 4 + (F[i * 6 + 3] - '0') * 2 + (F[i * 6 + 4] - '0'); if(S[i][x][y] >= 0 && S[i][x][y] <= 9) ret += (S[i][x][y] + '0'); else if(S[i][x][y] == 10) ret += "A"; else if(S[i][x][y] == 11) ret += "B"; else if(S[i][x][y] == 12) ret += "C"; else if(S[i][x][y] == 13) ret += "D"; else if(S[i][x][y] == 14) ret += "E"; else ret +="F"; } // cout << "Right After S-Box: " << ret << endl; string chaP = HextoBin(ret); //还差P变换 // cout << "Before P: " << chaP << endl; string ans(32, '0'); for(int i = 0; i < 32; i++) { ans[i] = chaP[P[i]]; } // cout << "f: " << ans << endl; return ans; }
运行结果
明文：
密钥：
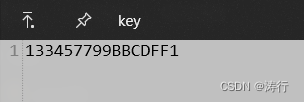
加密：
结果：
解密：
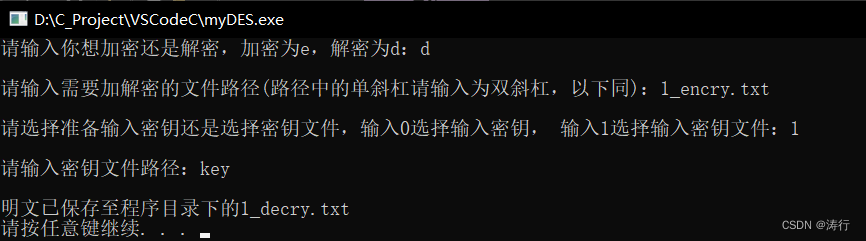
结果：
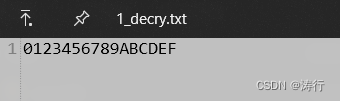
最后
以上就是标致蜜蜂最近收集整理的关于DES算法详细步骤以及C++代码实现详细步骤代码实现的全部内容，更多相关DES算法详细步骤以及C++代码实现详细步骤代码实现内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复