中国地质大学（武汉）计算机图形学备考

三视图投影，hermite三次样条，贝塞尔曲线，编码裁剪，二维矩阵变换，中点BH算法画直线，圆，椭圆，有效边表。

选择填空题（来自于曾经的考题）

1.与X扫描线多边形填充算法相比，改进的有效边表算法的主要优点是（计算量小，速度快）。

2.与参数表示法相比，图形的点阵表示法的主要缺点是（占存储空间大）。

3.三视图的主要优点和缺点是（可以精确丈量尺寸，但不直观）。

4.直线扫描转换的中点BH算法之所以便于用硬件实现，，是因为该算法（消灭了实数运算）。

5.用中点BH算法画圆时，之所以能够只扫描八分之一的圆，是因为（采用八分法画圆）。

6.与正轴测图相比，透视投影图的效果更（接近人的视觉效果）。

7.采用内存画图的两个主要优点是（显示速度快，便于保存最终结果）。

8.编码裁剪算法之所以适用于小裁剪窗口，是因为大部分线段可以（简弃处理）。

9.图形反走样的目的是为了（消除图形的走样现象）。

10.投影变换分为（平行投影和透视投影）两类。

11.x扫描线多边形填充算法中计算量大的环节是求交点。

12.与第四题对应，与DDA算法相比，改进的BH算法的主要优点是（消灭了实数运算）。

13.简单的光栅图形显示子系统与常用的光栅图形显示子系统的主要差别是（前者比后者少一个帧缓存）。发展的.....与常用的.....的主要差别是（前者比后者多一个处理器及其存储器）。

14.图形变换中引入规范化齐次坐标的目的是（使图形变换统一为矩阵相乘的形式）。

15.二维编码裁剪中，对一段线简取的条件是（code1|code2==0)，对一线段简弃的条件是（code1&code2不等于0）。

16.图形消隐的主要目的是（消除隐藏线与隐藏面）。

17.用离散量表示连续量引起的失真称为（走样）。克服.......称为（反走样）。

18.不属于直视存储管图形显示器特点的是（刷新速度快）。

19.采用逐行扫描和隔行扫描的图形显示器是（光栅扫描图形显示器）。

20.二位观察中引入规格化设备坐标系是为了使得（观察变换与设备无关）。

21.视区不变窗口变大，视野会变大，物体会变小。

22.三维观察中引入规范化投影空间的目的是（便于裁剪）。

23.图形的扫描转换是指在光栅显示器等数字设备上确定一个（最佳逼近图形的像素集）。

24.改进的有效边表能提高效率的最基本原因是（利用了扫描线与多边形边的连贯性）。

25.二维裁剪中如果裁剪窗口大，适合的裁剪方法是（编码裁剪）。

26.交互式计算机系统应该具有（计算，存储，交互，输入，输出）功能。（计，存，交，输，输）

27.形体的定义和图形的输入输出都是在一定的坐标系下进行的，这些坐标系分为（建模坐标系，用户坐标系，观察坐标系，规格化设备坐标系，设备坐标系）。

28.扫描线填充过程可分为（找交点，排序，交点配对，区间填充）。

29.基本几何变换都是相对于（坐标原点）和（坐标轴）进行的几何变换。

大题：

1.深度缓存器消隐算法的基本原理：

栈缓冲区和深度缓冲区，分别用于存放各个像素点的颜色值和对应的深度值，在进行多边形的扫描转换时，每当往帧缓冲区中存入一个颜色值之前，首先取出深度缓冲区中相应的深度值进行比较，若处理点的深度值大于深度缓冲区中相应点的深度值，则同时更新两个缓冲区的内容，否则放弃该点。 用这样的深度比较来实现消隐就是深度缓冲区算法的基本原理。

总结：首先是两个缓冲区存放像素点的颜色值和深度值。然后说在进行转换时，往帧缓冲区存颜色之前，跟深度缓冲区中对应深度值进行比较，若处理点的深度值大，更新两个缓冲区中的内容，否则放弃。

2.画家消隐算法的基本原理：

算法按多边形距离视点的远近进行深度排序，扫描转换按从远到近的顺序进行，对于重叠区域，将由离视点近的多边形覆盖离视点远的多边形区域，也就是以覆盖的方法达到消隐的目的。

总结：先说明算法按距离视点的远近进行深度排序，因为扫描转换按照从远到近的顺序进行，再说对于重叠区域，由离视点近的多边形覆盖离视点远的区域。

3.阴极射线管由哪些部分组成？它们的功能分别是什么？

CRT由电子枪，聚焦系统，偏转系统和荧光屏四部分组成。电子枪：用来产生游离电子。聚焦系统：将游离电子汇聚成一条细线。偏转系统：用来控制电子束的运动方向。荧光屏：受到电子束的轰击产生光点。

4.三个光栅系统分辨率依次为：640*480，1280*1024，2560*2048.欲存储每个像素12位，这些系统各需要多大的帧缓冲器？

640*480*12/8，1280*1024*12/8，2560*2048*12/8.

5.总结一下有效边表算法这类大题的注意点。

※首先画出边表。边表的画法就是从最小的y值画到最大的y值，然后填那4个格子的时候注意顺序是     x，y的最大值，k的倒数，箭头。

※如果两个边都在扫描线下面或者都在上面，y最大值不用-1，如果是一上一下的情况，y的最大值注意-1。

如果遇到了平行于扫描线的边，可以不用管。

※在画普通边表时是按x顺序画，画活性边表时注意按照斜率倒数的大小来排列顺序，同时，如果普通边表斜率算错了如果活性表按照普通边表斜率算就错完了，所以计算斜率时需要仔细一点。

6.关于矩阵变换类的题目

※1.首先将变换中心移回原点，变换操作后再移回原来的位置。

※2.关于二维旋转矩阵，我一般是按照从上到下，从左到右的顺序直接记忆（cos,-sin,sin,cos)。像这样的基础矩阵万一记错了麻烦就大了。注意旋转方向，绕原点顺时针旋转角度是负数，逆时针旋转角度是正数。

※3.二维的话，就是将各个坐标后面加一个1，构成矩阵后与已经计算好的矩阵相乘就可以算出变换后的坐标了。

※4.关于x轴对称，矩阵对角线上为（1，-1，1），关于y轴对称（-1，1，1），关于原点对称（-1，-1，1），关于y=x对称，矩阵为0 1 0，关于y=-x对称，矩阵为 0 -1 0.

                           1 0 0                                        -1 0 0 

                           0 0 1                                         0 0 1

※5.错切变换：矩阵为 1 b 0,c是沿着x方向，b是沿着y方向，比例变换 sx 0 0或者1 0 0，其中s大于1是缩小.

                                    c 1 0                                                                   0 sy 0        0 1 0

                                    0 0 1                                                                   0  0 1        0 0 S

7.关于裁剪的大题：

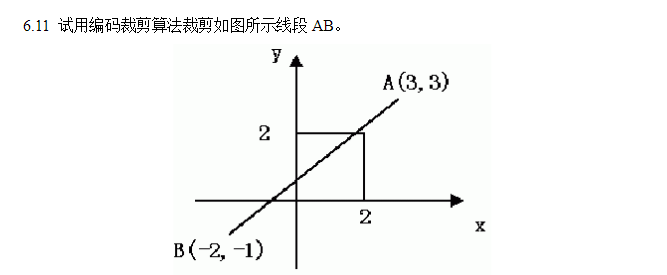
1.首先对AB进行编码，（窗口内的编码为0000，这四位从右往左依次是左右下上。）A的编码code1为1010，B的编码为 0101.由于code1|code2不等于0（如果等于0说明全都是0，那么就简取），且code1&code2=0（如果不等于0，说明有1，线段两个端点都在窗口外的同一侧，那么就简弃）所以既不能简取也不能简弃。

2.求交处理：A的编码为1010，右起第二位编码不为0，故求出直线段AB与窗口右边界的交点C（2，11/5）。C的编码为1000，编码不为0，求出来的是虚交点，继续求交，C的最高位不为0，求线段和窗口上边界的交点D（7/4，2），其编码为0000，此时AD必在窗口外，舍弃AD，用D代替A，code1等于0000.由于code1|code2不等于0，code1&code2等于0，线段AB依然不能简取简弃。。

3.求交处理。A（D）点的编码为0000，交换code1与code2的值以及AB点的坐标值，保证起点在窗口外，此时code1=0101，code2=0000.

由于code1=0101，右起第一位编码不为零，所以求出直线段A(B)B（D）与窗口左边界的交点E（0，3/5），E点的编码为0000，EA在窗口外，简弃处理，用E点坐标代替A点坐标和编码。由于code1|code2=0，直线段A(E)B(D)可简取。

总结：首先对AB进行编码，通过或与运算说明既不能简取也不能简弃。根据A点编码看从哪个边界开始求交点，如果求的是虚交点，那么还要根据虚交点的编码继续求交，一直到得到编码为0000的交点，然后简弃相应线段，用这个交点代替A点，此时code1为0000.再对code1，2进行或与运算,还不能直接简取，交换AB的编码和坐标，继续根据编码1位置求交点，一直求到编码为0000的交点，得到简取结果。

8.WA裁剪算法：

选定逆时针或者顺时针进行处理。如果是从窗口外进入窗口内，输出窗口内的部分。如果是从窗口内进入窗口外，输出内点到交点，交点到直角顶点，直角顶点到另一个交点。如果是窗口外进入窗口内再进入窗口外，一样是要找距离最近的交点。

9.三次样条：

1.已知给出三个坐标点PO(4,4)，P1(24,4)，P2(36,3)以及它们的斜率D0(8.832,5.547),D1(8.832,-5.547),D2(8.832，5.547).用其作为型值点来构造一条三次Hermite样条,写出曲线的函数,并计算参数分别为0，1/3，2/3，1时的值各为多少，并画出曲线。

这种题怎么做呢？

题目要求是1.写出曲线的函数2.计算参数分别为xxx时的值各为多少3.画出曲线

※1.曲线的函数：三次样条的构造P（u）=PkH0(u)+P(k+1)H1(u)+DPkH2(u)+DPk+1H3(u)

Pk和P（k+1）是坐标点，DPk和DPk+1是坐标点处的导数值。

题目三个坐标点将线段分成了两段，分别对这两段进行计算。

对P0,P1段，我们已经知道了P0和P1的坐标，需要求出P0.25，P0.5,P0.75，的坐标来画出图像。而这几处的坐标需要我们记住一个矩阵。或者说记住一个式子：hermite基函数：H0（t）=2t^3-3t^2+1,                     H1(t)=-2t^3+3t^2,                H2(t)=t^3-2t^2+t,              H3(t)=t^3-t^2。这个有百分之九十的概率考的，所以是一定要记住的。有了这四个式子之后，通过代入对应的参数0.25，0.5，0.75就可以算出对应的H0,H1,H2,H3。再将这些H带入P（t）这个公式中，就可以的到对应点处的坐标。这只是完成了第一段P0P1，对于P1P2段，进行同样的处理。这样的话，我们就可以得到所有的点了，然后就可以把这条边描出来了！

10.给定四点P1（0，0，0），P2（1，1，1），P3(2,-1,-1)，P4（3，0，0），用其作为特征多边形来构造一条三次贝塞尔曲线，写出曲线的参数方程，并计算参数分别为0，1/3，2/3，1时的值各为多少？

这种题怎么做呢？

一个三次贝塞尔曲线的参数方程是：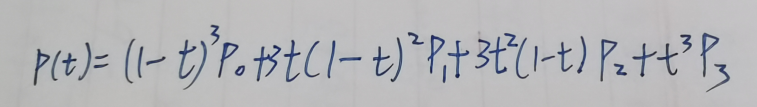

然后参数取0和1时分别是起点P1和终点P4。

在参数t取1/3时，带入上图中的公式，可以得到一个坐标。同样的将t取2/3还得到一个结果。这样参数为0，1/3，2/3，1时的结果都有了。

总结：做上面两道题一定要记住两个式子。第九题P（u）=PkH0(u)+P(k+1)H1(u)+DPkH2(u)+DPk+1H3(u)，然后H0（t）=2t^3-3t^2+1,                     H1(t)=-2t^3+3t^2,                H2(t)=t^3-2t^2+t,              H3(t)=t^3-t^2。

第十题要记住

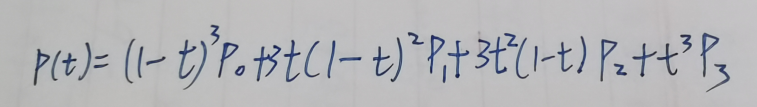
11.透视投影，考试的话老师说只考一点透视。

先看看三维情况下的基本变换。

平移比例旋转都写一张图上了。

三视图投影：

主视图1 0 0 0   俯视图1  0  0    0      侧视图0      0   0    0

           0 0 0 0              0 0 -1    0                -1      0   0   0 

           0 0 1 0              0 0  0    0                 0      0   1   0

           0 0 0 1              0 0 -Z0  1                -X0   0  0     e1

最后

以上就是怕孤单牛排为你收集整理的中国地质大学（武汉）计算机图形学备考的全部内容，希望文章能够帮你解决中国地质大学（武汉）计算机图形学备考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。