概述
和组合电路不同，当输入改变时，输出并不会马上改变。而是需要时钟信号改变时，输出会更新。
需要时序电路的原因很简单：当我们需要一个循环时，我们希望控制循环的变量是离散的。
如果i=1时进行循环，如果i=1的时间较长，可能会循环多次（由电路内部的延时决定）
但是如果是i的上升沿进行循环，可以给i的脉冲信号，方便控制循环的次数。
元件
锁存器
当时序信号高时输出，时序信号低时将新的输出"锁住"。
对应的verilog描述为
always@(clk)begin
....
end
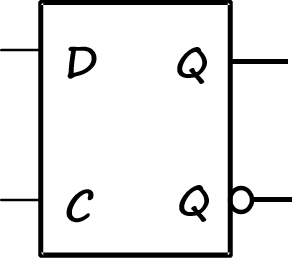
D锁存器，c为时序信号，当c为高时，把D输出到Q
触发器
锁存器的组合，即上升沿时被触发
对应的verilog描述为:
always@(posedge clk)begin
...
end
可以有多种实现，比如
SR主从触发器
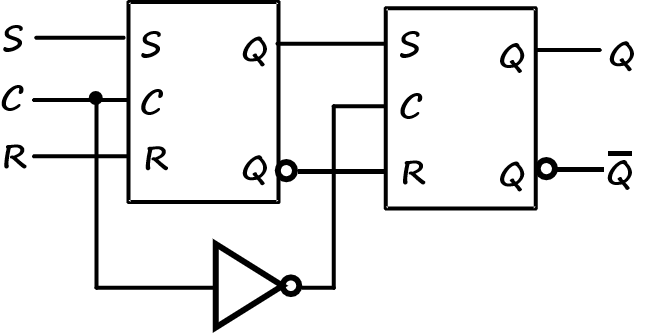
当c为高时，前一个加载，后一个锁住。
当c为低时，后一个加载，前一个锁住。
实现了下降沿的触发。
符号为：
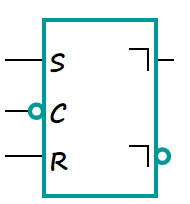
右侧的符号意味着下降沿触发，加反意味着上升沿触发。
S=1代表次态为1，R=1代表次态为0，R=0,S=0代表保持，不能同时为1
D边沿触发器
实现了类似的功能。
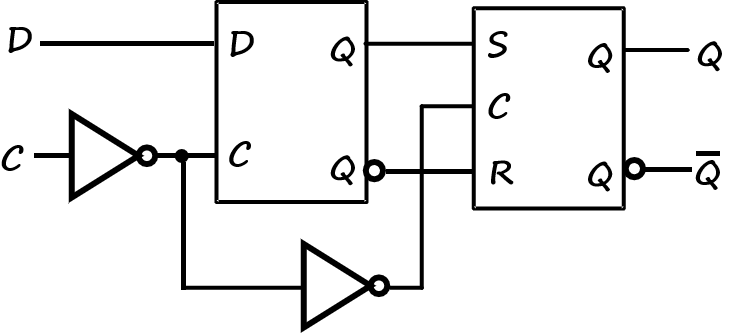
将时序信号加反可以得到上升沿触发
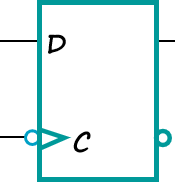
C意味着上升沿触发，加反就是下降沿触发。
由于initial 不可被初始化，所以加一个逻辑初始化，使其开始时在某个给定的状态。
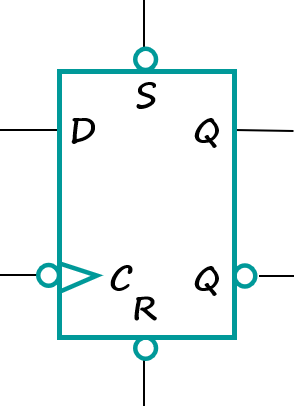
S输入0，非一下为1，可以使得Q初始化为1.
R输入0,非一下为1，可以使得Q初始化为0.
相当于：
always@(posedge clk or ~S or ~R ) begin
if(~S )
Q = 0;
else if(~R)
Q = 1;
else
...
end
JK触发器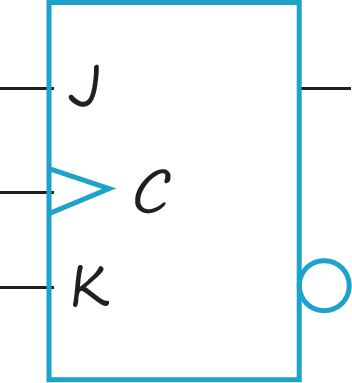
和SR触发器相同，J等效Set,K等效Reset，但是J=1,K=1时状态转相反。
T触发器
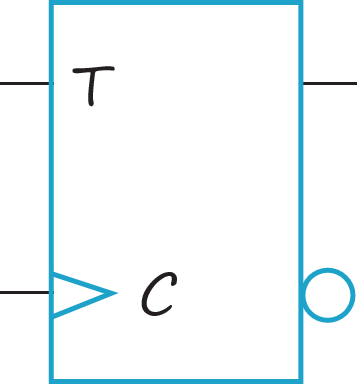
T=0状态报持，T=1状态反转。
电路分析
次态方程
每一个锁存器的输出都是一个状态A(t+1)
所以一个电路有几个锁存器就有几个状态。
锁存器的D输入为A(t)，输入为x(t)，输出为y(t),锁存器的输出为A(t+1)
状态表（Model State table）
需要包含现态，次态，输入，输出。
状态表有两种类型，摩尔型(Moore )和梅林型(Mealy)，摩尔型的输出只与状态有关，梅林型的输出和状态和输入有关。
首先分为三栏，第一栏是现态，第二栏是次态，第三栏是输出。
现态栏横着列出所有的状态，次态栏先列出输入，再在每一个输入中列出所有的状态，输出栏列出所有的输入，在输入中列出输出。
假如有A,B,C三个状态，如果给了是一个电路图，状态就是明确的输出。
如图所示：
| Present State | Next State | Output | ||||||||
| A | B | C | x=1 | x=0 | x=1 | x=0 | ||||
| A | B | C | A | B | C | y | ||||
| 0 | 0 | 0 | 1 | |||||||
如果给了一种描述，则可以：
| Present State | Next State | Output | ||
| x=1 | x=0 | x=1 | x=0 | |
| A | ||||
| B | ||||
| C | ||||
状态图
每种状态的取值用一个点表示。如果是摩尔类型，则是状态/输出。
比如三个状态：ABC，则有8种取值，因此有8个点。
从现态到次态的输入和输出用一条有向边表示。即：输入/输出
时间
:信号进入第一个锁存器所需要的时间
:信号从第一个锁存器到第二个锁存器所需要的时间
:信号经过第二个锁存器所需要的时间
:时钟周期减去总延迟和建立时间之和，即空余的时间
:时钟周期
:hold time：使得锁存器停止的时钟信号出现到锁存器真正被锁住的时间。
有关系：
为了在一个周期中使得信号能够经过两个锁存器，要求：
The longest path from an external input to a positive clock edge：从外部输入到锁存器输出的最长延迟。
最大的频率：要求是锁存器输出到锁存器输出的最大延迟的倒数。
状态设计
给定一个描述，可以根据描述的任务画出状态图。
比如要求匹配序列1101，则可以设定4个状态。初始状态，得到了1,得到了11，得到了110，得到了1101
如果最后一个1可以被后一次利用，那么得到了1101就是状态得到了1
可以将3个状态命名为A,B,C,D，然后画出状态图和状态表。
状态简化
将等效的状态进行合并，可以减少状态，从而减少触发器的数量。
等效的状态：输出相同，
并且有以下三种之一
a,次态相同
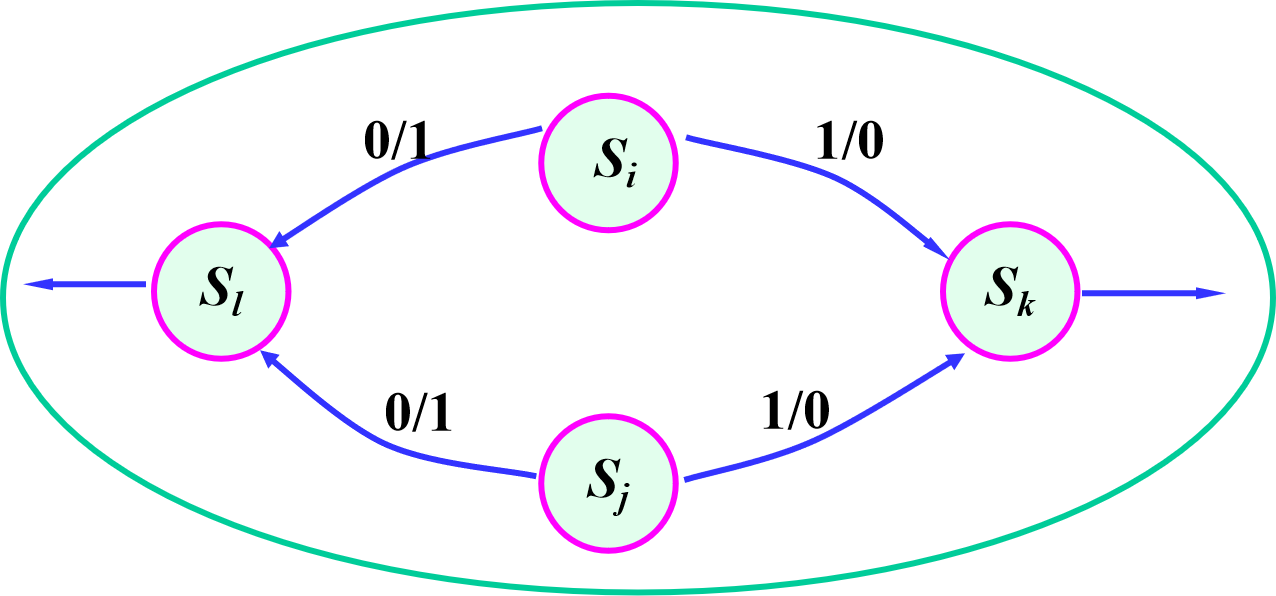
b,次态交错（a->b,b->a）则a,b等效
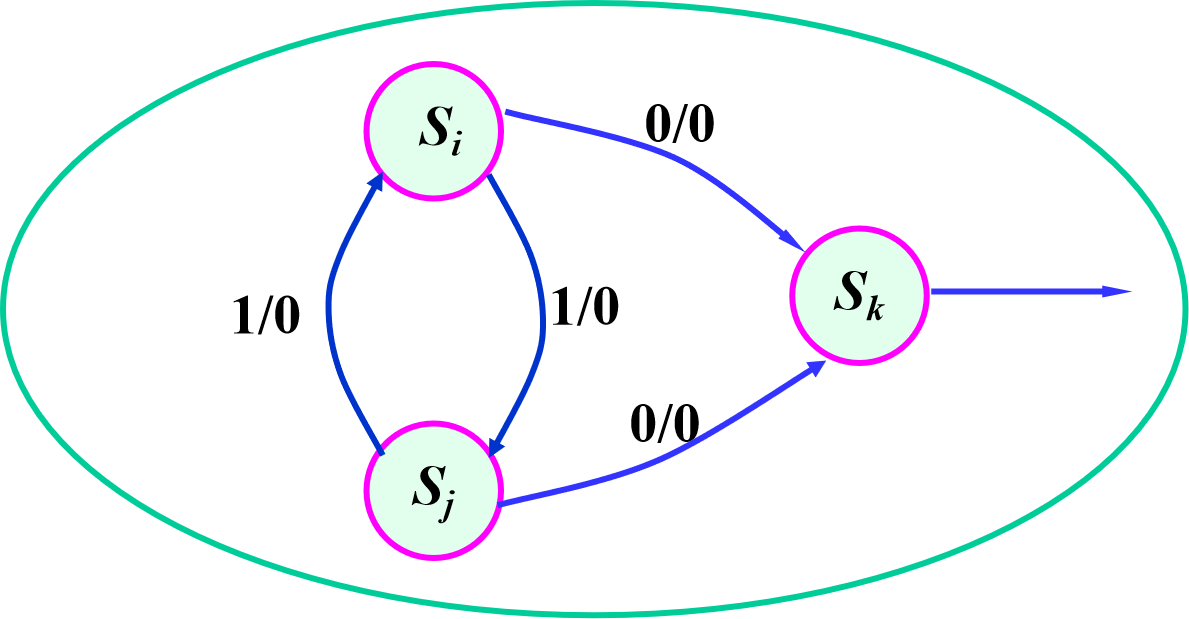
c,次态循环（若次态AB等效，则CD等效并且有若CD等效，则AB等效）
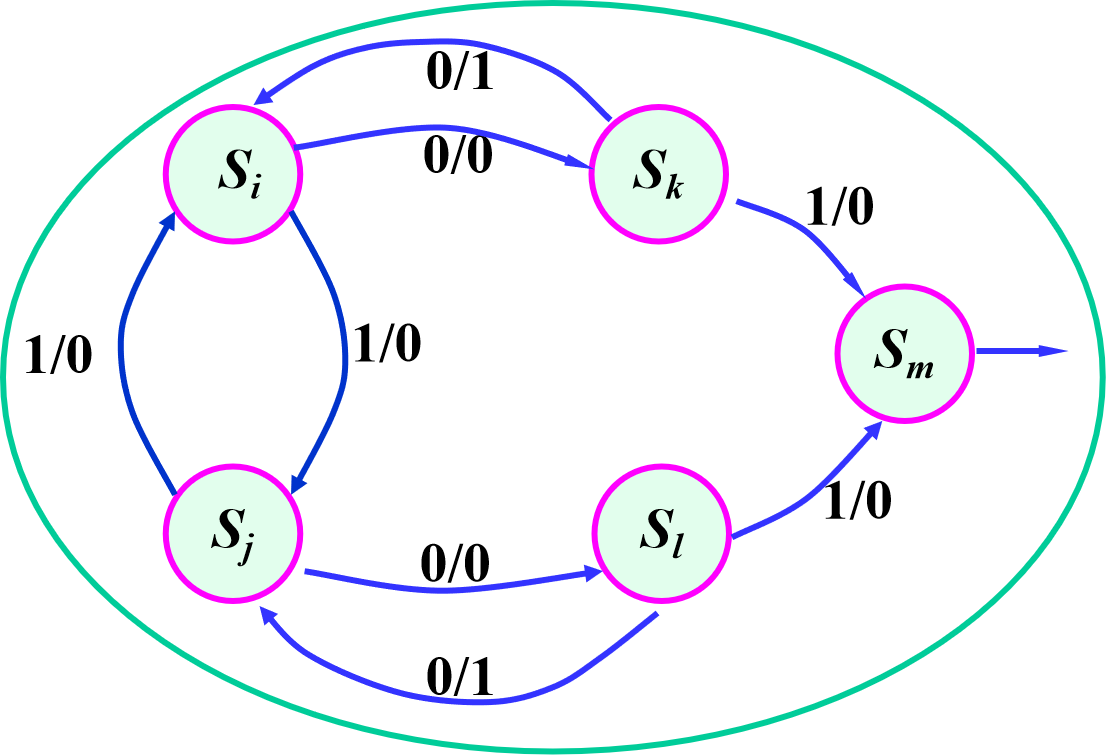
隐含表法：
将状态列为一个下三角矩阵除去对角线的部分，若行列的状态等效则打勾，若不等效则打叉。
若不能确定则写上决定它们是否等效的那个状态。
若有次态ABCDE,则隐含表如下
| A | ||||
| B | 1 | |||
| C | 1 | 1 | ||
| D | 1 | 1 | 1 | |
| A | B | C | D |
隐含表可以得到若干个等效对，将等效对合并为等效类，即可得到若干个等效类。将其命名为新的状态。
状态分配
若将每一个状态分配一个二进制码，则不同的分配方式使得电路代价不同。
为了减少代价，依据以下分配方法：
1.相同输入时，相同次态分配相邻的二进制码
2.相邻输入时，相同现态的次态分配相邻的二进制码
3.输出相同的现态分配相邻的二进制码
4.出现次数最多的次态分配二进制码0
若有4个次态，画出2*2的方格，则行列第一第二分格分别代表0,1，将次态填入方格，方格的行列即为二进制码。
最后
以上就是跳跃诺言为你收集整理的数逻第四章 时序电路 元件电路分析时间状态设计状态简化状态分配的全部内容，希望文章能够帮你解决数逻第四章 时序电路 元件电路分析时间状态设计状态简化状态分配所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复