时序逻辑电路
- 集成触发器
- 触发器
- 基本RS触发器
- TTL集成主从触发器
- 集成边沿触发器
- CMOs触发器
- 时序逻辑电路分析
- 同步时序电路分析方法
- 异步时序逻辑电路分析方法
- 常用时序逻辑电路设计
- 序列信号发生器
- 一般时序逻辑电路的设计方法
- 一般同步时序逻辑电路的设计方法
- 异步计数器设计
集成触发器
触发器
- 触发器状态方程: Q n + 1 = f ( Q n , X ) Q^{n+1}=f(Q^n,X) Qn+1=f(Qn,X), 也叫特征方程
基本RS触发器
{
Q
n
+
1
=
S
+
R
ˉ
Q
n
R
⋅
S
=
0
begin{cases}Q^{n+1}=S+bar RQ^n\Rcdot S=0end{cases}
{Qn+1=S+RˉQnR⋅S=0
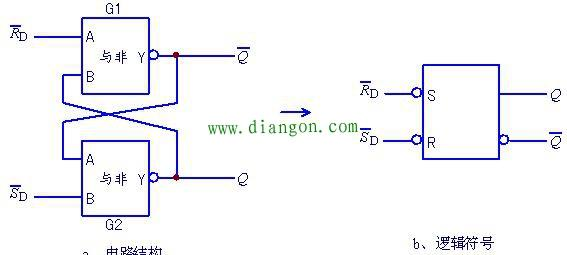
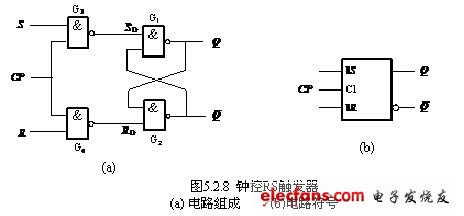
- 钟控RS触发器:
- 钟控D触发器
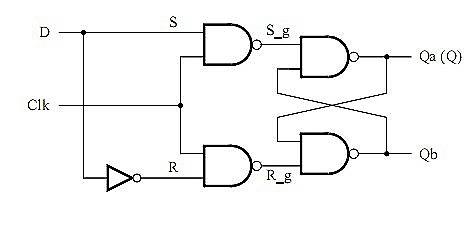
输 Q n + 1 = D Q^{n+1}=D Qn+1=D - 钟控JK触发器:
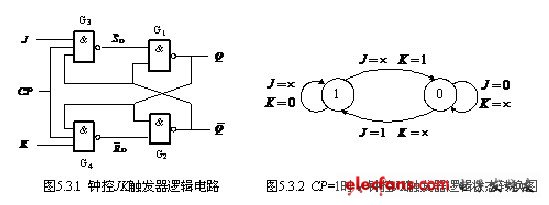
输出为 Q n + 1 = J Q ˉ n + K ˉ Q n Q^{n+1}=Jbar Q^n+bar K Q^n Qn+1=JQˉn+KˉQn - 钟控T触发器
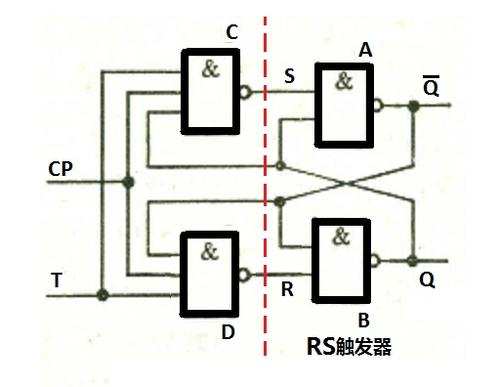
状态方程: Q n + 1 = Q ˉ n Q^{n+1}=bar Q^n Qn+1=Qˉn
TTL集成主从触发器
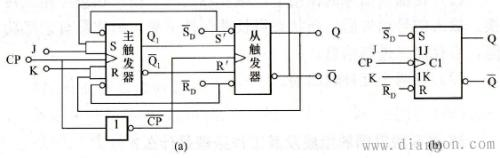
- 主从JK触发器输出变化的时刻在时钟的下降沿
- 输出变化方向:
- 若在CP等于1期间, JK信号不变, 由CP下降沿的JK值决定输出状态
- 若在CP=1期间, JK信号发生变化, 则符合以下规律:
- CP=1之前, 若Q=0, 则看CP=1期间的J信号, 若J有1出现, 则CP下降时Q一定为1, 否则Q保持0.
- CP=1之前, 若Q=1, 则看CP=1期间的K信号, 若K有1出现, 则CP下降时Q一定为0, 否则Q保持1.
- 异步置0置1输入
集成边沿触发器
- 负边沿JK触发器: 只有时钟下降前的JK值才能对触发器起作用并引起翻转, 实现了边沿触发JK触发器的功能.
- 维持-阻塞D触发器: 只有在时钟上升沿前的D信号才能进入触发器并引起翻转, 故为边沿型触发器.
CMOs触发器
- CMOS钟控D触发器: CP=1时, 触发器保持原状态, CP=0时, 具有D触发器的功能
- CMO主从D触发器: 上升沿具有D触发器的功能. 特点有: 1. 异步置0和置1高电平有效, 而不是低电平有效;2. 状态翻转时刻是上升沿;3. 不存在一次翻转
- CMO主从JK触发器: JK触发器是在CMOS主从D触发器的基础上更改的, D = J Q ˉ n + K ˉ Q n D=Jbar Q^n+bar K Q^n D=JQˉn+KˉQn
时序逻辑电路分析
- 激励方程: Y = f ( X , S n ) Y=f(X,S^n) Y=f(X,Sn)
- 状态方程: S n + 1 = h ( X , S n ) S^{n+1}=h(X,S^n) Sn+1=h(X,Sn)
- 输出方程: Z = g ( X , S n ) Z=g(X,S^n) Z=g(X,Sn)
- 激励方程使输入方程, Y为各输入端函数的集合. 状态方程为输出方程, 使输入与现在状态的方程.
- 时序电路可以没有组合逻辑电路部分, 但储存逻辑电路必不可少
- 米里型电路: 输出信号不仅取决于储存电路的状态, 而且还取决于输入变量
- 摩尔型电路: 输出信号仅仅取决于储存电路的状态 ,与输入信号无关.
- 集成D触发器特指芯片上的每个触发器有互补的两个输出, 而锁存器和寄存器没有互补输出.
- 同步计数器运行速度比异步更快.
同步时序电路分析方法
- 分析步骤:
- 根据给定的时序电路, 写出每个触发器的输入激励方程
- 根据电路, 写出时序电路输出方程
- 由激励方程和特征方程, 写出触发器的状态方程(即下一状态方程)
- 由状态方程和时序电路的输出方程做出电路的状态转移表和状态转移图.
- 根据具体要求和电路状态特点, 分析电路完成具体的逻辑功能
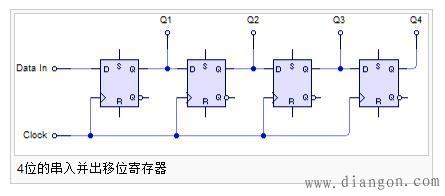
- 位移寄存器:
- 环形计数器:
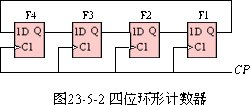
为环形计数器添加自启动能力: 画出卡诺图, 找到一不确定触发器输入点, 将该输入点改为1, 且该点应与原化简圈相邻, 此时得到的反馈项可使计数器拥有计数能力. 推广到一般: 对于由 Q 0 , Q 1 , . . . Q k − 1 Q_0,Q_1,...Q_{k-1} Q0,Q1,...Qk−1k个D触发器构成的环形计数器, 反馈得到的函数应为 D 0 = Q ˉ 0 n Q ˉ 1 n . . . Q ˉ k − 2 n D_0=bar Q_0^nbar Q_1^n...bar Q_{k-2}^n D0=Qˉ0nQˉ1n...Qˉk−2n
- 扭环计数器
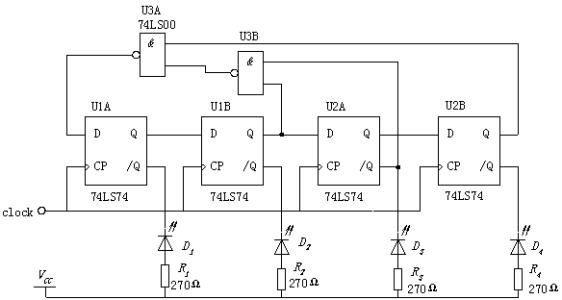
扭环计数器特点:- 不考虑自启动时, k位触发器构成的环形计数器反馈连接方式是 D 0 = Q ˉ k − 1 n D_0=bar Q_{k-1}^n D0=Qˉk−1n, 其内部仍然是移位寄存器的连接方式
- k个触发器构成的扭环计数器有2k个状态构成工作循环, 模值M=2k, 比环形计数器多一倍.
- 一般选取包含全0状态和全1状态的2k个工作循环, 可以从全0状态或全1状态中的一个来推导出全部技术状态.
- 扭环计数器构成脉冲分配器时的译码电路不论k等于多少, 每个状态的译码输出函数都是两变量函数. 脉冲分配器: 使用模值M的计数器加译码器产生M个输出, 即每个状态对应一个输出, 且只在该状态下输出为1(或为0), 其他状态下输出0(或为1).
- 直接按照 D 0 = Q ˉ k − 1 n D_0=bar Q_{k-1}^n D0=Qˉk−1n方式连接的扭环计数器时不能自启动的, 需要采取额外措施, 方法同上问环形计数器, 增加非工作状态到化简圈中.
- 序列信号发生器: 产生一组循环长度为M的, 有规律的串行序列信号的时序逻辑电路, 使用移存器和适当的反馈电路可以构成移存器型序列信号发生器.分析时, 如果发生器全部由D触发器构成,且反馈电路较简单, 可不做出状态转移表, 而直接从起始状态开始, 根据反馈函数的逻辑关系, 逐位的写出全部序列信号.
异步时序逻辑电路分析方法
- 分析步骤
- 写出激励方程, 状态方程, 输出方程
- 由外部时钟提供时钟沿触发的触发器, 各个时钟沿均有效
- 设定电路的初始状态(例如0000), 填入状态表的现状态列的第一行, 根据激励方程和状态方程求出由外部时钟提供触发的触发器的下一状态, 填入下一状态列的第一行.
- 对于某一级触发器曲子前级输出作为时钟时, 需要根据前级时钟的变换, 确定是否有有效时钟, 如果有有效时钟, 则根据激励方程和状态方程求其新状态, 没有有效时钟是, 状态不变.
- 将求出的新状态作为先状态, 重复第4部, 依次求出各触发器的下一状态, 直到状态转移表出现重复状态.
- 选取不在上述循环中的某一状态作为现状态, 重复上述工作, 最终完成状态转移表.
常用时序逻辑电路设计
- 常用时序逻辑电路设计步骤
- 根据设计要求, 作出状态转移表
- 根据状态转移表, 作出以现状态为输入, 下一状态为输出的卡诺图, 从卡诺图求出电路的状态方程, 同时, 作出电路输出的卡诺图, 求出输出方程
- 由状态方程直接求出触发器的输入激励方程, 完成触发器输入逻辑的设计
- 根据设计结果, 画出状态转移图, 由于一般设计要求中, 指定了工作状态的转移关系, 所以要将所有状态的转移关系表示清楚. 检查能否自启动, 若不能, 还要重新修改某个触发器的激励方程.
- 根据激励方程和输出方程, 选择器件, 完成具体逻辑设计, 画出最后得到的逻辑图.
序列信号发生器
- 由计数器与译码电路构成的序列信号发生器: 计数器的设计与上文相同, 译码电路的设计即将计数器的输出作为译码器的输入, 按照计数器的状态顺序和所要求的序列信号给出的真值表求解输出即可
- 由移位寄存器加反馈电路构成的序列信号发生器: 对于计数器来说, 计数模值M和触发器数目k之间一定满足
2
k
−
1
<
M
≤
2
k
2^{k-1}<Mleq 2^k
2k−1<M≤2k. 而由移存器构成的序列信号长度不一定满足此关系, 取决于序列信号的具体形式, 设计步骤也有所变化:
- 根据给定序列长度确定所需要的最少触发器数目k
- 以k个信号为一组, 确定第一组后, 向后移一位, 共取M组, 如果M组状态不重复, 可选择k个触发器, 否则k增加一位, 重复上述过程.
- 最终得到M组状态, 就是序列信号发生器的状态转移关系, 将它们依次排列, 构成这个序列信号发生器反馈函数的真值表, 真值表左边为按状态转移顺序纵向排列转移, 右边是这个状态下反馈信号值 D 0 D_0 D0, 在使用D触发器的情况下, 这个反馈值就是 F F 0 FF_0 FF0触发器的下一状态 Q 0 n + 1 Q_0^{n+1} Q0n+1
- 由反馈函数的真值表求出反馈函数 D 0 D_0 D0
- 检查不使用状态的状态转移关系
- 画逻辑图
一般时序逻辑电路的设计方法
一般同步时序逻辑电路的设计方法
- 设计步骤:
- 建立电路原始状态图或状态表: 把要实现的时序逻辑功能表示为时序逻辑函数, 可以用状态表的形式, 也可以用状态图的形式. 这需要
1. 分析逻辑问题, 确定输入, 输出变量以及电路状态数, 通常取原因或条件为输入变量, 结果作输出变量
2. 定义输入/输出逻辑状态和每个电路状态的含义, 并将电路状态顺序编号
3. 按照题意列出电路原始状态表或原始状态图 - 状态简化: 若设计中出现两个状态在相同的输入下由相同的输出, 并且转换到同样下一状态, 则称这两个状态等价, 等价状态可以合并为一个
- 状态分配: 又称状态编码. 时序逻辑电路的状态是用触发器状态的不同组合来表示的.
1. 确定触发器的数目k, k个触发器共有2^k种状态组合, 所以为获得时序电路所需的M个状态, 应该取 2 k − 1 < M ≤ 2 k 2^{k-1}<Mleq 2^k 2k−1<M≤2k
2. 给每个电路状态规定对应的触发器状态组合, 称为状态编码 - 选定触发器类型, 求出电路的状态方程, 驱动方程和输出方程
- 画出逻辑图
- 检查能否自启动
- 建立电路原始状态图或状态表: 把要实现的时序逻辑功能表示为时序逻辑函数, 可以用状态表的形式, 也可以用状态图的形式. 这需要
- 状态分配:
- 行相邻原则: 当两个或两个以上的状态在相同输入的情况下有相同的下一状态, 它们的代码尽可能安排为相邻代码.
- 列相邻原则: 对于每个现状态在相邻输入组合之下的下一状态不同, 给这些下一状态以相邻编码.
- 输出相邻原则: 若两个后两个以上的现状态在同意输入组合下有相同的输出时, 应给予相邻的编码.
异步计数器设计
最后
以上就是贪玩毛巾最近收集整理的关于数电(四)时序逻辑电路集成触发器时序逻辑电路分析的全部内容,更多相关数电(四)时序逻辑电路集成触发器时序逻辑电路分析内容请搜索靠谱客的其他文章。








发表评论 取消回复