数电基础知识

（一）时钟信号特性有：抖动(Jitter)、偏移（skew）、占空比失真(Duty Cycle Distortion)

1.偏移SKEW

    因时钟线长度不同或负载不同，导致时钟到达相邻单元的时间不同，这个时间上的偏差就叫时钟偏移SKEW。　　　

 

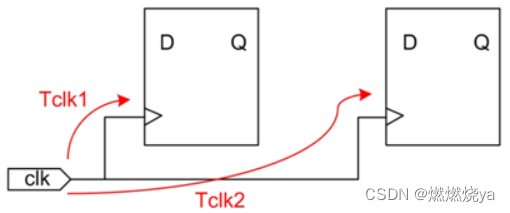
    在上图中的Tskew=Tc1-Tc2

    偏移会一直存在，因此FPGA在设计时，会进行优化，采用全铜工艺和树状结构，设计专门的始终缓冲和驱动网络，使得时钟到达不同单元时的路径一样长，尽量减小偏移。

所以，Skew 问题的解决方法就是：设计中的主要信号应该走全局时钟网络。

此外FPGA中延迟锁定环（Delay locked ring,DLL）也可以去SKEW，延迟锁相环由控制逻辑和延时线组成，控制逻辑将输入时钟与输出时钟进行比较，并插入延时从而使得时钟同步。

    但无论如何，在STA时，任然要考虑Skew。

2.抖动Jitter

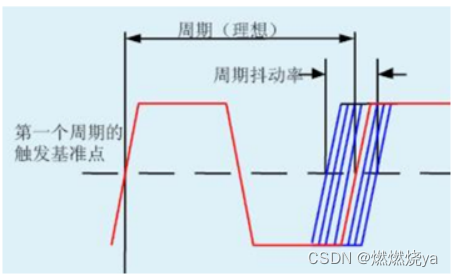
    在理想情况下，一个频率固定的完美的脉冲信号（以1MHz为例）的持续时间应该恰好是1us，每500ns有一个跳变沿。但这种信号并不存在。如图所示，信号周期的长度总会有一定变化，从而导致下一个沿的到来时间不确定。这种不确定就是抖动（jitter）。时钟抖动也永远存在。

3.占空比失真Duty Cycle Distortion

 

    占空比失真即时钟不对称，高电平和低电平时间发生变化。DCD会占用时间裕量（Slack）造成数字信号的失真，使过零区间偏离理想的位置。DCD通常是由信号的上升沿和下降沿之间时序不同而造成的。

（二）扇入扇出Fan-in/Fan-out

   数字电路中，逻辑门相互连接，每个逻辑门输出端与输入端都连着大量别的单元，因此由扇入扇出表示处理外部输入以及驱动外部其他单元的能力。

1.亚稳态及相关概念

   同步电路中：

　　建立时间（Setup time）：触发器时钟上升沿到来前数据保持稳定的时间。

　　保持时间（Hold time）：触发器时钟上升沿到来后数保持据稳定的时间。

 

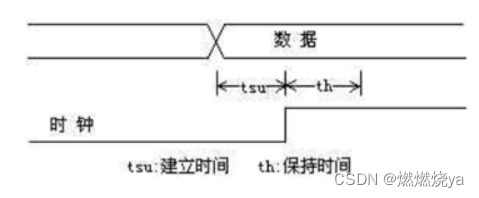
　如图所示，在时钟上升沿到来前后的一段时间内数据必须保持稳定，否则数据就无法写入，造成“亚稳态“输出。如果前级驱动够强劲，电路就能按照趋势变化下去，一定时间后该点的值就会变化为“正确值”，如果驱动不够强劲，电路就会恢复之前的值，最终得到何值是不可控的，所以我们要避免亚稳态。在使用DFF时，必须满足其建立时间和保持时间的要求。　　　　　　

 

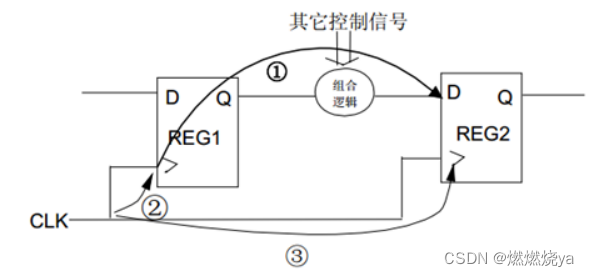
以上图为例，假设时序如下

 

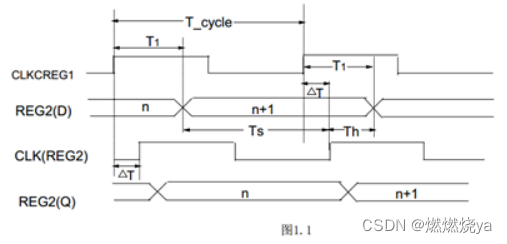
在上图时序中：

△T=Tskew（skew和时钟抖动jitter有区别）

T1=REG1检测到时钟后内部延时+组合逻辑延时最后到达REG2的时间

Tcycle=CLK的周期

Tsu=数据在CLK2上升沿到达前维持的时间

Tsu = Tcycle + Tskew-T1

Th=数据在CLK上升沿到达后维持的时间

    Th = T1 – Tskew

　如果Ts>setup time(触发器)，Th>hold time（触发器）则数据能正常写入，由这个条件可以看出，Tskew与T1起着关键作用，而正之前所说如果使用全局时钟则Tskew会很小，可以忽略不计。

 实例：

 

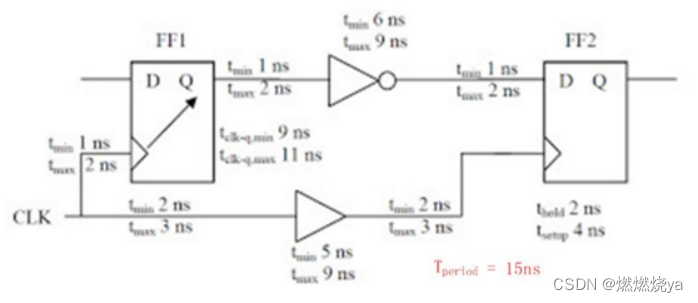
　　以上图为例Tsu= Tcycle + Tskew-T1要使Tsu最小，则Tskew最小，T1最大。

Tsu(min) = Tcycle + Tskew(min)-T1(max)=15+2+5+2-2-11-2-9-2<Tsetup

因此发生了setup violation

2.异步复位时：

　　　　除了同步电路中会产生亚稳态外（不满足Tsu和Th），在异步复位时也会产生亚稳态，这里需要提到复位时间与撤销时间。

复位时间（recovery）：复位信号释放（对于低电平有效的复位信号指上升沿），与紧跟其后的第一个时钟上升沿之间的最小时间。

撤销时间（removal）：时钟信号的上升沿，与紧跟其后异步复位信号从有效到无效的最小时间。　　　　

 

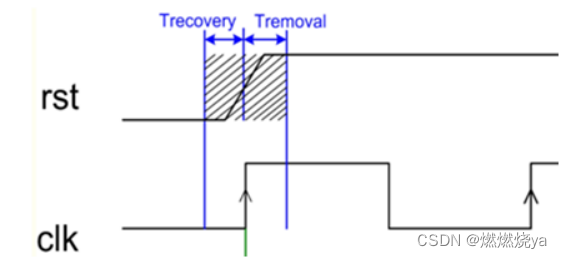
　　如图所示，异步复位信号撤销必须在复位时间和撤销时间外，否则会产生亚稳态。　　　　

 

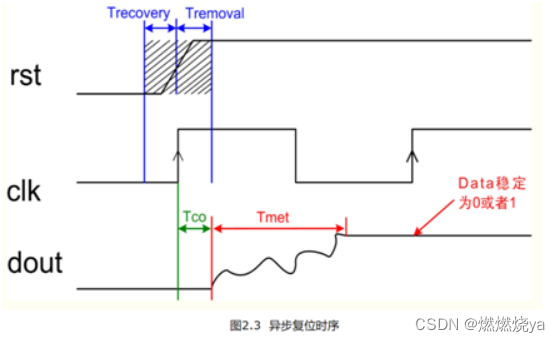
　　异步复位信号撤销时间在Trecovery和Tremoval之内，则会造成亚稳态，在时钟上升沿Tco（输出延时）后会产生振荡，振荡时间为Tmet（决断时间）。

• 寄存器中的亚稳态

1.只要系统中有异步元件，亚稳态就是无法避免的，亚稳态主要发生在异步信号检测、跨时钟域信号传输中。

2.对于同步信号而言不满足Tsu和Th会产生亚稳态，对于异步信号，复位不满足Trecovery和Tremoval会产生亚稳态。

3.随着clk频率的增加，亚稳态发生的几率是增加的。

 4.采用工艺更好的FPGA。

消除亚稳态方法：

1.对异步信号进行同步处理；

2.使用FIFO对跨时钟域数据进行缓冲处理；

3.复位电路采用异步复位，同步释放处理；

（四）时间裕量Slack

 1.时间裕量分析首先需要将电路中的路径找出来。路径的起点有两种：时序器件的时钟输入端、电路的起点；终点也有两种：时序器件的数据输入端、电路的终点。如下图所示，一共有四种路径。

 

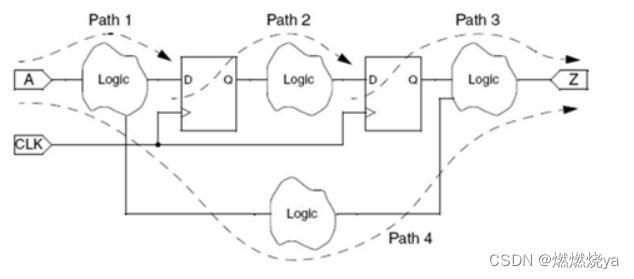
 除了路径外还有以下几个概念需要了解：

  关键路径(critical path)：从输入到输出中延时最大的那条路径。

   到达时间(arrival time)：信号从参考的时间起到达某特点位置的时间。

   需求时间(required time)：信号到达的最晚的时间。

   时间裕量(slack)：用需要时间减去到达时间得到的结果就是时间裕量（slack =required time- arrival time）。如果时证书则说明路径延时满足需求，如果时负数则说明延时不满足。其中比较重要的时Hold Time Slack。

计算：

仍然以该电路为例　　

 

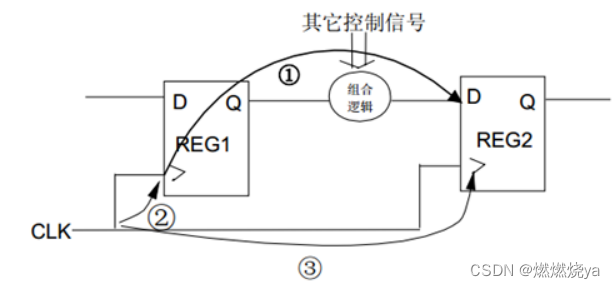
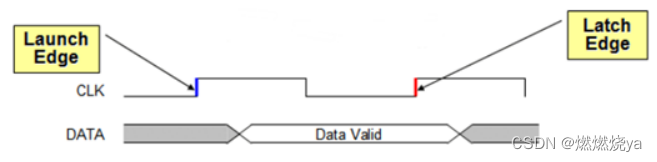
　发射沿(Launch Edge)：产生数据的REG1的clock上升沿；

    锁存沿(Latch Edge)：接受数据的REG2的clock的上升沿，延时Launch Edge1个时钟；

 

数据到达时间（Data Arrival Time）

 

 

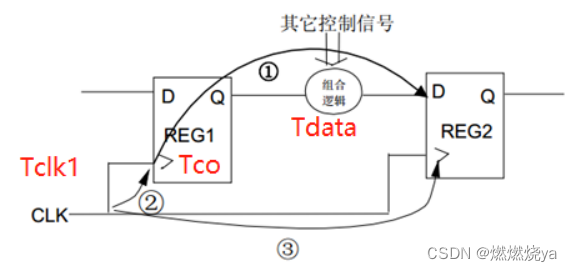
 Tclk1= CLK到达REG1的时间

Tco  = REG1固定延时

Tdata= 数据传输时间

    时序图如下：

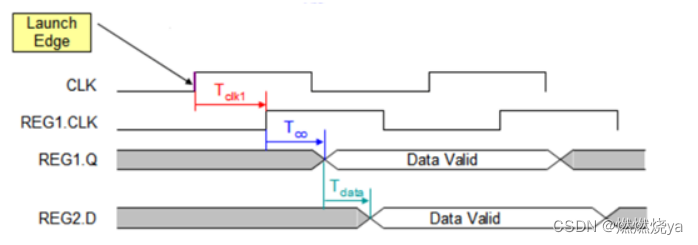
  Data Arrival Time = Launch Edge+Tclk1+Tco+Tdata 

时钟到达时间（Clock Arrival Time）

 

 

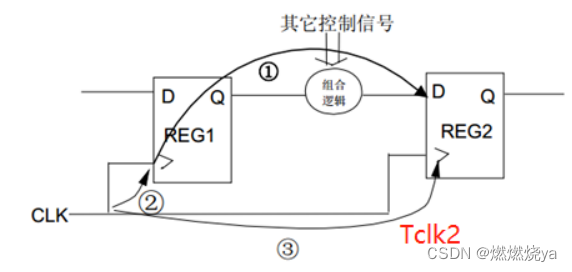
时序图如下：

 

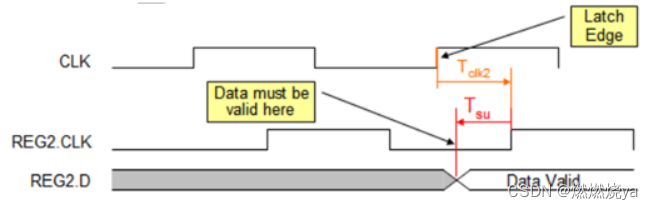
Clock Arrival Time = latch Edge+Tclk2

 

数据建立需求时间（Data Required Time Setup）

      因为数据必须在Tsu之前有效，因此:

       Data Required Time Setup = Clock Arrival Time-Tsu

数据保持需求时间（Data Required Time Hold）

      因为数据必须在Th之后才能改变，因此：

  Data Required Time Hold= Clock Arrival Time+Th

   最后计算Slack

    Setup Slack = Data Required Time Setup -Data Arrival Time

     Hold Slack = Clock Arrival Time - Data Required Time Hold

（五）Cell延时

我们都知道在数字IC设计流程中cell（std，IO，IP）的时序（timing）、面积（area）、功能（functionality）和功耗（power）信息都包含在lib库里面，其中时序信息最为关键。

 

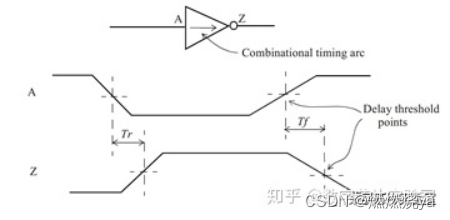
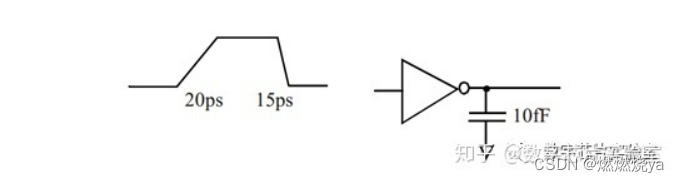
以最简单的反相器为例，所谓cell的时序信息，即图中的传播延时Tr和Tf

• Tr : Output rise delay

• Tf : Output fall delay

反相器cell的延时取决于两个因素：

输出负载（output load），即输出引脚的电容负载输入信号的过渡时间（input transition time）

延迟值与负载电容直接相关。负载电容越大，延迟越大。

在大多数情况下，延迟随着输入transition time的增加而增加，但是延迟和输入transitiontime并不总是单调关系，尤其是在输出负载较小的情况下。

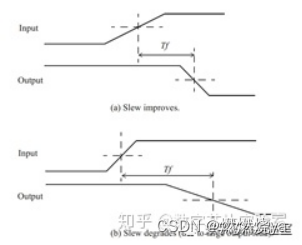
输出的transition time主要取决于输出电容，随输出负载而增加。因此，较大的输入transition time可以根据cell的类型及其输出负载不同得到改善。

早期的延时建模采用简单的线性延迟模型（linear delay model），其中延迟是input transition time和output load capacitance两者的线性函数，其一般形式如下所示：

 

D = D0 +D1 * S + D2 * C

其中D0，D1，D2是常数，S是inputtransition time，C是output load capacitance。

线性延迟模型在亚微米工艺下不太准确，因此目前大多数lib库使用更复杂的模型，例如非线性延迟模型(non-lineardelay model)。

Non-LinearDelay Model

大多数lib库都包括查找表模型(table models)，例如NLDM（非线性延迟模型），为cell的各种时序弧（timing arcs）指定延迟，output transition和其他时序检查等信息。

• Risedelay

• Fall delay

• Rise transition

• Fall transition

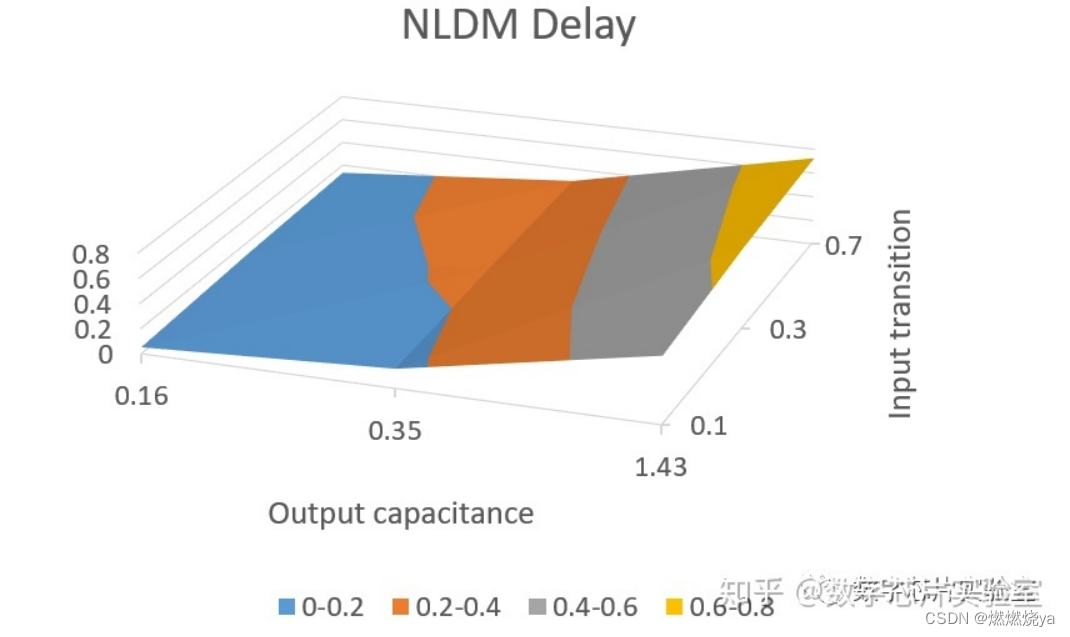
LDM根据input transition time和output capacitance获得cell的不同timing arcs的延迟。也就是说，NLDM模型是一个二维的查找表，其中两个输入变量是inputtransition time和output capacitance，表中的内容是该timing arcs的延迟。

 

lu_table_template(delay_template_3x3) {

variable_1 : input_net_transition;

variable_2 :total_output_net_capacitance;

index_1 ("1000, 1001,1002");

index_2 ("1000, 1001,1002");

}/* The input transition and the output capacitance can be

in either order, that is, variable_1 can be the output

capacitance. However, these designations are usually

consistent across all templates in a library. */

上面的查找表模板指定表中的第一个行索引变量是input transition time，第二个列索引变量是output capacitance。索引值（1000, 1001, 1002）只是模板，会被实际索引值覆盖。

下面是实际的NLDM

pin(OUT) {

max_transition : 1.0;

timing() {

related_pin : "INP1";

timing_sense : negative_unate;

cell_rise(delay_template_3x3) {

index_1 ("0.1, 0.3, 0.7");/* Input transition */

index_2 ("0.16, 0.35,1.43"); /* Output capacitance */

values ( /* 0.16 0.35 1.43 */

/* 0.1 */ "0.0513, 0.1537, 0.5280",

/* 0.3 */ "0.1018, 0.2327, 0.6476",

/* 0.7 */ "0.1334, 0.2973, 0.7252");

}

cell_fall(delay_template_3x3) {

index_1 ("0.1, 0.3, 0.7");/* Input transition */

index_2 ("0.16, 0.35,1.43"); /* Output capacitance */

values ( /* 0.16 0.35 1.43 */

/* 0.1 */ "0.0617, 0.1537, 0.5280",

/* 0.3 */ "0.0918, 0.2027, 0.5676",

/* 0.7 */ "0.1034, 0.2273, 0.6452");

}

在上面的例子中，描述了输出引脚OUT分别在上升（cell_rise）和下降（cell_fall）的从引脚INP1到引脚OUT的延迟。还指定了输出引脚OUT的max_transition。查找表模板已经在delay_template_3x3中描述。

表中的timing_sense : negative_unate表示输入的翻转和输出翻转是相反的关系，即

input rise -> output fall

input fall -> output rise

根据延迟表，对于反相器的cell_rise延迟，input transition（fall） time为0.3ns，output load为0.16pf 时，对应延迟为0.1018ns。

 

NLDM模型不仅用于延迟，而且还用于指定output transition time，该值也是以input transition time和output load为索引变量的查找表。

pin(OUT) {

max_transition : 1.0;

timing() {

related_pin : "INP";

timing_sense : negative_unate;

rise_transition(delay_template_3x3) {

index_1 ("0.1, 0.3, 0.7");/* Input transition */

index_2 ("0.16, 0.35,1.43"); /* Output capacitance */

values ( /* 0.16 0.35 1.43 */

/* 0.1 */ "0.0417, 0.1337, 0.4680",

/* 0.3 */ "0.0718, 0.1827, 0.5676",

/* 0.7 */ "0.1034, 0.2173, 0.6452");

}

fall_transition(delay_template_3x3) {

index_1 ("0.1, 0.3, 0.7");/* Input transition */

index_2 ("0.16, 0.35,1.43"); /* Output capacitance */

values ( /* 0.16 0.35 1.43 */

/* 0.1 */ "0.0817, 0.1937, 0.7280",

/* 0.3 */ "0.1018, 0.2327, 0.7676",

/* 0.7 */ "0.1334, 0.2973, 0.8452");

}. . .

}

. . .

}

最后

以上就是忧虑蓝天为你收集整理的数电基础知识的全部内容，希望文章能够帮你解决数电基础知识所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。