数字电子技术——逻辑代数与EDA技术的基础知识

一、进制转换

任意进制数(N进制)展开式的普通表达式：
$$D=\sum k_i{N}^i$$
进制转换详情

1.1 常见的几种编码

1.1.1 十进制代码

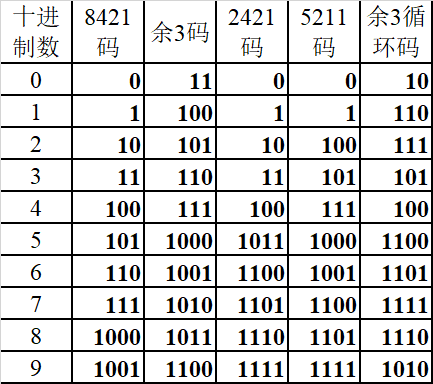
说明：
余三码：由8421BCD码加上0011形成的一种无权码，即其值比原值大3。
2421码：从左到右，第一位权值为2，第二位的权值为4，第三位的权值为2，第四位的权值为1。
5211码：从左到右，第一位权值为5，第二位的权值为2，第三位的权值为1，第四位的权值为1。
余三循环码：从三开始计数。

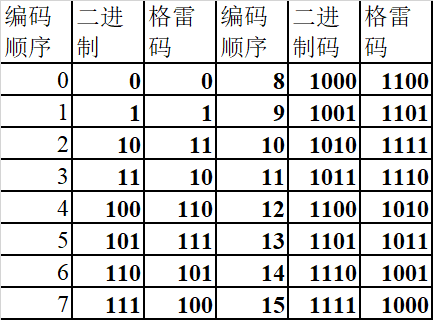
1.1.2 格雷码

特点：
1.每一位的状态变化都按一定的顺序循环。
2.编码顺序依次变化，按表中顺序变化时，相邻代码只有一位改变状态。
应用：减少过渡噪声

二、逻辑代数的基本概念、公式和定理

2.1 基本逻辑运算

在逻辑代数中，基本逻辑运算有与、或、非三种。常见的逻辑运算时与非、或非、与或非、异或等。

2.2 三种逻辑关系

2.2.1 与逻辑关系

$$Y=A\cdot B$$

2.2.2 或逻辑关系

$$Y=A+B$$

2.2.3 非逻辑关系

$$Y=\bar{A}$$
如果此处还有疑问，可以尝试画真值表来进一步理解。

2.2.1~2.2.3为逻辑表达式，A、B为输入逻辑变量，Y为输出逻辑变量。字母上面无反号的称为原变量，有反号的称为反变量。

2.3 常用的逻辑运算

（1）与非运算
$$Y=\overline{A\cdot B}$$
（2）非运算
$$Y=\overline{A+B}$$
（3）与或非运算
$$Y=\overline{A\cdot B+C\cdot D}$$
（4）异或运算
$$Y=\bar{A}\cdot B+A\cdot \bar{B}=A\oplus B$$

2.4 部分公式

$$\begin{array}{rl}A+\bar{A}& =1\\ (A\cdot B)& =A\cdot (B\cdot C)\\ A\cdot (A\cdot B)& =A\cdot B+A\cdot C\\ A+B\cdot C& =(A+B)\cdot (A+C)\end{array}$$

2.4.1 德摩·根定理

$$\begin{array}{rl}\overline{A\cdot B}& =\bar{A}+\bar{B}\\ \overline{A+B}& =\bar{A}\cdot B\end{array}$$

2.4.1 还原定理

$$\overline{\overline{A}}=A$$

三、两个重要规则

3.1 代入原则

如果等式两边所有出现某一变量的地方，都代之以一个函数，则等式仍然成立，这个规则称为代入规则。

3.2 反演规则

对于任意一个函数表达式Y，如果将Y中所有的“·”换成“+”，将“+”换成“·”；“0”换成“1”，“1”换成“0”；原变量换成反变量，反变量换成原变量，这个规则称为反演规则。

四、逻辑函数的化简方法

4.1 公式化简

4.2 卡诺图化简

以2ⁿ个小方块分别代表 n 变量的所有最小项，并将它们排列成矩阵，而且使几何位置相邻的两个最小项在逻辑上也是相邻的（只有一个变量不同），就得到表示n变量全部最小项的卡诺图。

最后

以上就是务实保温杯为你收集整理的数字电子技术——逻辑代数与EDA技术的基础知识的全部内容，希望文章能够帮你解决数字电子技术——逻辑代数与EDA技术的基础知识所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。