摘要:本节首先介绍有关数制和码制的一些基本概念和术语,然后给出常用的数制和码制。此外,还将具体讲述不同数制之间的转换方法和二进制数算术运算的原理和方法。
基本概念
数码:数字编码。既可以用来表示数量的多少。也可以用来表示不同的事物或事物不同的状态。
数制:用数码表示数量的大小时,仅仅使用一位数码往往不够用,因而经常需要用进位计数制的方法组成多位数码使用。多位数中每一位的构成方法和从低位到高位的进位规则被称为数制。
代码:在用不同数码表示不同的事物或事物不同的状态时,这些数码已经不再具有表示数量大小的含义了,它们只是不同事物的代号而已。我们将这些数码称之为代码。
码制:为了便于记忆和查找,在编写代码时要遵循一定的规则,这些规则称为码制。
常用数制
十进制: 0 1 2 3 4 5 6 7 8 9 10
二进制: 0 1 10
八进制: 0 1 2 3 4 5 6 7 10
十六进制:0 1 2 3 4 5 6 7 8 9 A B C D E F 10
普遍形式: ,
称为计数的基数,
为第
位的系数,
称为第
位的权。
数制转换
2,8,16进制刚好互为整数倍,转换较为简单。
2,8,16转换为10进制时,可以将2.8.16位进制的数按位展开相加即可。
10进制转2,8,16进制时,可以先将10进制转为2进制,之后再转为其他进制。
10进制转2进制,整数部分用除法。余数倒序排列。小数部分用乘法,乘出的整数正序排列。
以上只为了手工计算方便,主要原因是我们的大脑熟练于10进制的加减乘除运算,因此任意进制的数制转换时,都可以以10进制作为桥梁。
二进制算术计算
因为计算机采用二进制,所以这里对二进制的算术运算进行描述
四则运算:与十进制完全相同,区别只在于“逢二进一”。
原码:第一位为符号位,符号位为0表示正数,为1表示负数。
补码:正数的补码等于原码,负数的补码为原码按位取反再加1.(符号位不变)
反码:正数的反码等于原码,负数的反码为原码按位取.(符号位不变)
几种常用的编码
十进制代码:用二进制代码表示十进制的0~9这十个状态,二进制代码至少应当有4位,4位二进制代码一共有十六个(0000~1111),去其中哪十个以及如何与0~9相对应,有许多种方案。
| 十进制数 | 8421码 (BCD码) | 余三码 | 2421码 | 5211码 | 余3循环码 |
|---|---|---|---|---|---|
| 0 | 0000 | 0011 | 0000 | 0000 | 0010 |
| 1 | 0001 | 0100 | 0001 | 0001 | 0110 |
| 2 | 0010 | 0101 | 0010 | 0100 | 0111 |
| 3 | 0011 | 0110 | 0011 | 0101 | 0101 |
| 4 | 0100 | 0111 | 0100 | 0111 | 0100 |
| 5 | 0101 | 1000 | 1011 | 1000 | 1100 |
| 6 | 0110 | 1001 | 1100 | 1001 | 1101 |
| 7 | 0111 | 1010 | 1101 | 1100 | 1111 |
| 8 | 1000 | 1011 | 1110 | 1101 | 1110 |
| 9 | 1001 | 1100 | 1111 | 1111 | 1010 |
| 权 | 8421 | 2421 | 5211 |
选用不同的编码均为了不同应用时的方便,比如8421码符合人们的习惯;余3码相加时,若两数之和等于10,正好等于二进制数的16,于是便产生进位信号,而且0和9、1和8、2和7、3和6、4和5的余三码互为反码,这对于求取对10的补码很方便;2421码中。0和9、1和8、2和7、3和6、4和5也互为反码。5211码与数字电路的计数器特性一致;余3循环码每相邻两代码之间只有一位的状态不同。
格雷码:又称循环码,最大的特点是每相邻两代码之间只有一位的状态不同。
| 编码顺序 | 二进制代码 | 格雷码 |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
美国信息交换标准代码(ASCII):
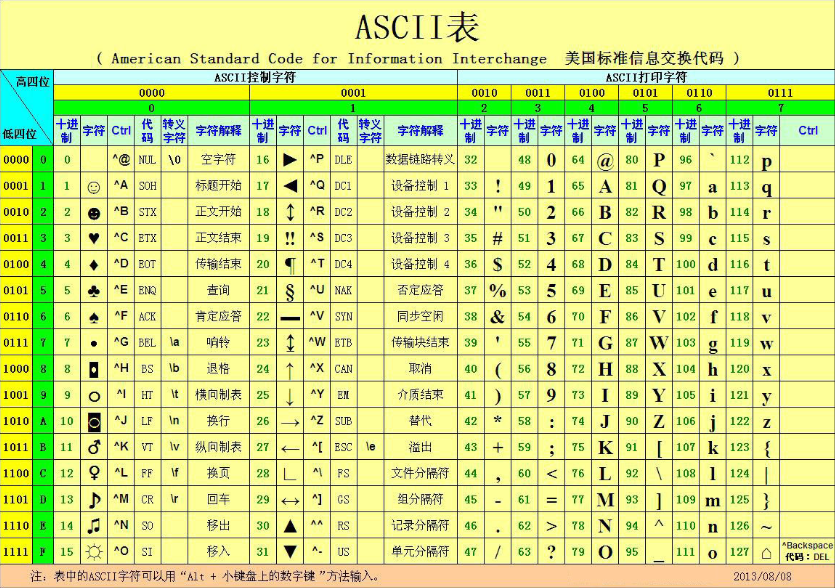
本节所列举的十进制代码、格雷码、ASCII码是基本常见的通用代码。此外,我们完全可以根据自己的需要,自行编制专用的代码。
参考链接
- 《数字电子技术基础》(第六版)高等教育出版社
- https://www.cnblogs.com/Rambotien/gallery/image/171201.html
最后
以上就是繁荣奇异果最近收集整理的关于数字电路-数制和码制的全部内容,更多相关数字电路-数制和码制内容请搜索靠谱客的其他文章。








发表评论 取消回复