机器学习之决策树

【前言】
机器学习中关于决策树、熵、信息增益等的相关介绍
更多文章：传送门

1.什么是决策树/判定树(decision tree)

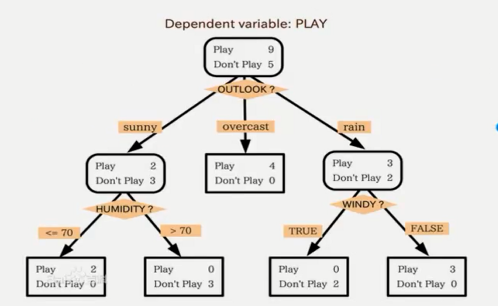
决策树是一个类似于流程图 的树结构，决策树由有向边和结点构成，决策树的结点有两种，一种是内部结点，一种是叶结点。分类决策树中，内部结点代表特征，叶结点代表类。回归树中，内部结点代表输入空间的划分区域，叶结点代表输出值。每个内部节点表示在一个属性上的测试，每个分支代表一个属性输出，而每个树叶节点代表类或类分布

• 决策树是一种既可以用于分类又可用于回归的算法
• 决策树可以认为是if-then规则，也可认为是输入空间和类空间条件概率
• 决策树的生成分为三步：特征值的选择，决策树生成，决策树剪枝
  

2. 基本概念

2.1 熵(entropy)

熵是表达随机变量不确定性的一种度量，熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大，因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
对于随机变量X，P(X=xi)=pi定义

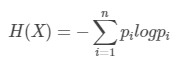
当对数以2为底时，单位为比特1bit=log2^2(log2以2为底)，当对数以e为底时单位为纳特。由定义可知，熵只和随机变量X的分布有关和X的取值无关。
例如：假设世界杯32支球队的概率相同，都为1/32，可计算

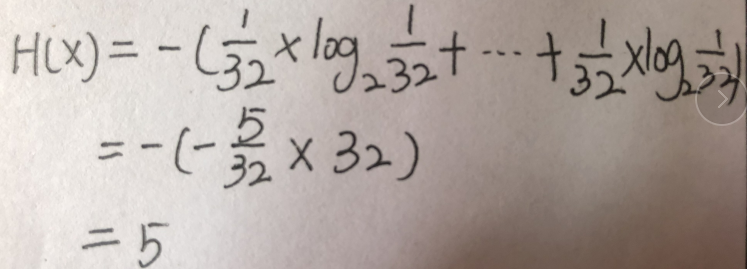
即说明可能需要经过5次的筛选（折半：16，8，4，2，1）最后得到结果（一支球队能否夺冠）

2.2 其他熵

更多熵概念信息如图所示：

3. 决策树归纳算法 (ID3)

3.1 信息获取量/信息增益(Information Gain)

简要介绍：
要建立的决策树的形式类似于“如果天气怎么样，去玩；否则，怎么着怎么着”的树形分叉。那么问题是用哪个属性（即变量，如天气、温度、湿度和风力）最适合充当这颗树的根节点，在它上面没有其他节点，其他的属性都是它的后续节点。借用信息论的概念，我们用一个统计量，信息增益Information Gain来衡量一个属性区分以上数据样本的能力 。信息增益量越大，这个属性作为一棵树的根节点就能使这棵树更简洁，比如说一棵树可以这么读成，如果风力弱，就去玩；风力强，再按天气、温度等分情况讨论，此时用风力作为这棵树的根节点就很有价值。如果说，风力弱，再又天气晴朗，就去玩；如果风力强，再又怎么怎么分情况讨论，这棵树相比就不够简洁了。计算信息增益的公式需要用到“熵”（Entropy）

3.2 信息增益的公式

Gain(A)=Info(D)-Info_A(D),代表通过节点A进行分类获取了多少信息（单位是bit）

• 解读：Info(D)代表仅仅按照标记来分的时候的所有信息熵
  Info_A(D)代表以特征A来分时的信息熵
  所以Gain(A)=Info(D)-Info_A(D)为二者差值的信息熵

3.3 信息增益的理解

对于待划分的数据集D，其 entroy(前)是一定的，但是划分之后的熵 entroy(后)是不定的，entroy(后)越小说明使用此特征划分得到的子集的不确定性越小（也就是纯度越高），因此 entroy(前) - entroy(后)差异越大，说明使用当前特征划分数据集D的话，其纯度上升的更快。而我们在构建最优的决策树的时候总希望能更快速到达纯度更高的集合，这一点可以参考优化算法中的梯度下降算法，每一步沿着负梯度方法最小化损失函数的原因就是负梯度方向是函数值减小最快的方向。同理：在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展，因此我们总是选择使得信息增益最大的特征来划分当前数据集D。

3.4 求信息增益最大特征

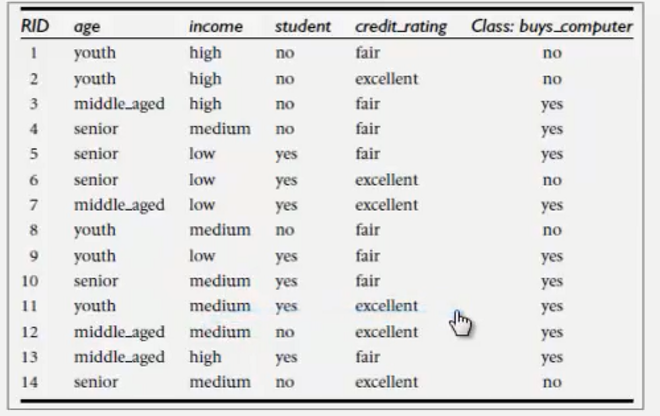
不考虑特征age,income,student,credit_rating的情况下，根据Class:buys_computer标记yes/no计算出的信息熵：

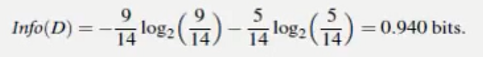
根据age特征计算出的信息熵：

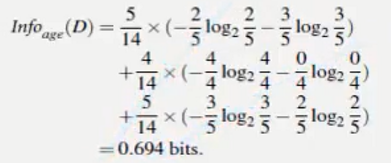
两者的差值：

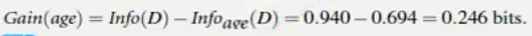
同理可计算出根据income,student,credit_rating的信息获取量为：

选择最大的信息获取量Gain(age)=0.246作为第一个根节点：

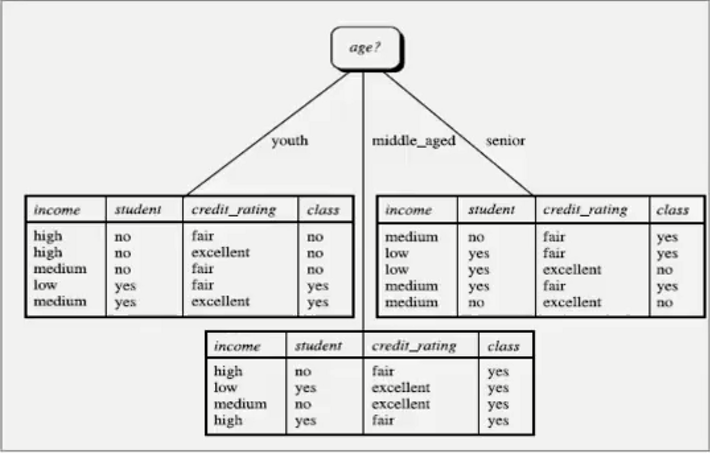
注：在训练集表中可以看到，age有三种分类，所以上图中以age为根节点的树中age下有三个分支

通过观察可知，middle_aged分支下class全部都是yes，所以没有必要在进行分支。而youth和senior分支下class还存在yes和no，需要进行递归处理。方法同上
不断重复这个过程，直到所有的叶子节点下class均为yes或者no
对算法的描述如下图：

3.5 信息增益的缺点及解决方法

信息增益缺点：信息增益偏向取值较多的特征
原因：当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益比较 偏向取值较多的特征。
解决方法：信息增益比

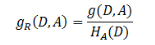
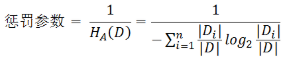
• 信息增益比本质： 是在信息增益的基础之上乘上一个惩罚参数。特征取值个数较多时，惩罚参数较小；特征取值个数较少时，惩罚参数较大。
• 惩罚参数：数据集D以特征A作为随机变量的熵的倒数，即：将特征A取值相同的样本划分到同一个子集中（数据集的熵是依据类别进行划分的）
• 信息增益比缺点：信息增益比偏向取值较少的特征 ，因为特征取值个数较少时，惩罚参数较大，由信息增益比 = 惩罚参数 * 信息增益知，取值较少的特征的信息增益比就越大。

3.6 其他算法

相同点：都是贪心算法，自上而下
不同点：属性选择 度量方法不同。C4.5(gain ratio),CART(gini index),ID3(Information Gain)
如何处理连续型变量的属性？设置阈值

4. 总结

优点：直观，便于理解，小规模数据集有效
缺点：处理连续型变量效果不好，类别较多时错误增长得较快，规模性一般

决策树相关文章

最后

以上就是结实小松鼠为你收集整理的机器学习之决策树的全部内容，希望文章能够帮你解决机器学习之决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。