照例,还是贴出大佬的博客地址:here。
决策树,我们可以简单的看作一个二叉树,在数据结构中我们都知道使用决策树可以很快的对一个数据进行二分查找,那么使用决策树进行预测(或者说分类)也是同理,只要使用数据建立了一颗二叉树,那么在下一个预测数据到达的时候,可以很快的对该数据进行分类。
1. 预备知识
1.1 熵
参考视频:here
熵是一个热力学概念的词,其物理意义是体系混乱程度的度量。在计算机中常用来表示随机变量的不确定性,定义如下:
H
(
p
)
=
−
∑
i
n
p
i
l
o
g
p
i
H(p) = -sum_i^np_i logp_i
H(p)=−i∑npilogpi
p
i
p_i
pi是一件事情发生的概率,其值我们都知道在0-1之间,那么,我们可以简单的定义一个事件的发生概率有两个,即:p和1-p,不妨来简单的绘制其图像:
此时的函数为:
y
=
−
(
x
l
o
g
x
+
(
1
−
x
)
l
o
g
(
1
−
x
)
)
y = -(xlogx+(1-x)log(1-x))
y=−(xlogx+(1−x)log(1−x))
即:
import numpy as np
import matplotlib.pyplot as plt
def getY(x):
return -(x * np.log(x) + (np.tile(1, x.shape)-x) * np.log(1-x))
x = np.linspace(0, 1, 200)
plt.plot(x, getY(x))
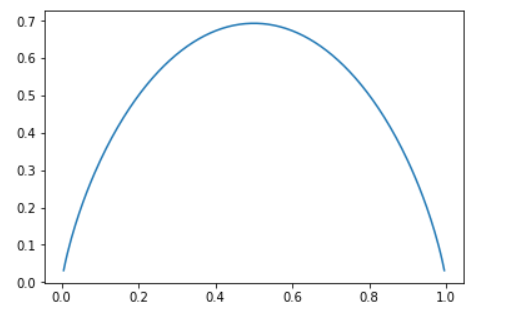
在
p
=
p=
p=0.5的时候,我们看到熵值最大,而在0.5的时候,我们知道事件的不确定性越高,也就是说熵值越大,其事件的不确定性程度也就越高,随机变量的不确定性就越大。
1.2 条件熵
条件熵 H ( X ∣ Y ) H(X|Y) H(X∣Y)表示在已知随机变量 Y Y Y的条件下,随机变量 X X X的不确定性。
????(X|Y)定义为在给定条件????下,X的条件概率分布的熵对Y的数学期望:
这里举个例子来表示,Y表示整个数据集,而X表示某一个特征,该特征的值可以分为三个类别,分别表示为
x
1
x_1
x1、
x
2
x_2
x2和
x
3
x_3
x3三类,那么我们计算在X这个特征下,这个数据集Y的熵,即条件熵,表示如下:
H
(
Y
∣
X
)
=
∑
i
=
1
n
p
(
x
)
H
(
Y
∣
X
=
x
)
=
∣
x
1
∣
∣
X
∣
H
(
Y
∣
X
=
x
1
)
+
∣
x
2
∣
∣
X
∣
H
(
Y
∣
X
=
x
2
)
+
∣
x
3
∣
∣
X
∣
H
(
Y
∣
X
=
x
3
)
begin{aligned} H(Y|X) &= sum_{i=1}^np(x) H(Y|X=x) \ &= frac{|x_1|}{|X|}H(Y|X=x_1) + frac{|x_2|}{|X|}H(Y|X=x_2) + frac{|x_3|}{|X|}H(Y|X=x_3) end{aligned}
H(Y∣X)=i=1∑np(x)H(Y∣X=x)=∣X∣∣x1∣H(Y∣X=x1)+∣X∣∣x2∣H(Y∣X=x2)+∣X∣∣x3∣H(Y∣X=x3)
不妨来举个栗子,如有下面的数据集:
| Id | 年龄段 | 性别 | 眼皮 | 喜欢吃 | 血型 | 有无高血压 |
|---|---|---|---|---|---|---|
| 1 | 0-20 | 男 | 单 | 肉 | AB | 没有 |
| 2 | 0-20 | 男 | 单 | 肉 | B | 没有 |
| 3 | 0-20 | 男 | 双 | 肉 | O | 有 |
| 4 | 20-50 | 男 | 单 | 菜 | AB | 有 |
| 5 | 50-100 | 男 | 单 | 都不 | O | 有 |
| 6 | 0-20 | 男 | 单 | 菜 | O | 有 |
假设有这么个数据集,在年龄段这个特征中,我们统计下可以知道可以分为3个类别,那么我们这里可以模拟计算下在已知数据集“年龄段”这个特征下,我们这个数据集的条件熵是多少。
这么说来可能比较抽象,换句话说,也就是了解下在这么多的特征中,那个特征可以很好的表示这个数据集
D
D
D本身的不确定性程度,即:在这里就是“年龄段
X
X
X”这个特征是否和患高血压有较强的关系。
不妨简单的计算下:
H
(
D
∣
X
)
=
∑
i
=
1
3
p
(
x
i
)
H
(
Y
∣
X
=
x
i
)
=
4
6
∗
H
(
Y
∣
X
=
x
(
0
−
20
)
)
+
1
6
∗
H
(
Y
∣
X
=
x
(
20
−
50
)
)
+
1
6
∗
H
(
Y
∣
X
=
x
(
50
−
100
)
)
begin{aligned} H(D|X) &= sum_{i=1}^3p(x_i) H(Y|X=x_i) \ &= frac{4}{6} * H(Y|X=x_{(0-20)}) + frac{1}{6} * H(Y|X=x_{(20-50)}) + frac{1}{6} * H(Y|X=x_{(50-100)}) \ end{aligned}
H(D∣X)=i=1∑3p(xi)H(Y∣X=xi)=64∗H(Y∣X=x(0−20))+61∗H(Y∣X=x(20−50))+61∗H(Y∣X=x(50−100))
而
H
(
Y
∣
X
=
x
(
0
−
20
)
)
H(Y|X=x_{(0-20)})
H(Y∣X=x(0−20))的计算,也就是在下面的子数据集下做计算即可:
| Id | 年龄段 | 性别 | 眼皮 | 喜欢吃 | 血型 | 有无高血压 |
|---|---|---|---|---|---|---|
| 1 | 0-20 | 男 | 单 | 肉 | AB | 没有 |
| 2 | 0-20 | 男 | 单 | 肉 | B | 没有 |
| 3 | 0-20 | 男 | 双 | 肉 | O | 有 |
| 6 | 0-20 | 男 | 单 | 菜 | O | 有 |
这个数据集的熵的计算就是在上面1.1中所介绍的计算方式,即:
y
=
−
(
x
l
o
g
x
+
(
1
−
x
)
l
o
g
(
1
−
x
)
)
y = -(xlogx+(1-x)log(1-x))
y=−(xlogx+(1−x)log(1−x))
这里没有发生的概率是
1
2
frac{1}{2}
21,那么该数据集的熵是:
y
=
−
2
∗
1
2
l
o
g
1
2
=
l
o
g
2
begin{aligned} y &= -2*frac{1}{2}logfrac{1}{2} \ &= log2 end{aligned}
y=−2∗21log21=log2
类似的,我们可以计算
H
(
Y
∣
X
=
x
(
20
−
50
)
)
H(Y|X=x_{(20-50)})
H(Y∣X=x(20−50)),即,
−
l
o
g
1
-log1
−log1
那么,我们可以接着写,即:
H
(
D
∣
X
)
=
∑
i
=
1
3
p
(
x
i
)
H
(
Y
∣
X
=
x
i
)
=
4
6
∗
H
(
Y
∣
X
=
x
(
0
−
20
)
)
+
1
6
∗
H
(
Y
∣
X
=
x
(
20
−
50
)
)
+
1
6
∗
H
(
Y
∣
X
=
x
(
50
−
100
)
)
=
2
3
∗
l
o
g
2
+
2
∗
(
−
l
o
g
1
)
=
0.46209812037329684
begin{aligned} H(D|X) &= sum_{i=1}^3p(x_i) H(Y|X=x_i) \ &= frac{4}{6} * H(Y|X=x_{(0-20)}) + frac{1}{6} * H(Y|X=x_{(20-50)}) + frac{1}{6} * H(Y|X=x_{(50-100)}) \ &= frac{2}{3} * log2 + 2 * (-log1) \ &= 0.46209812037329684 end{aligned}
H(D∣X)=i=1∑3p(xi)H(Y∣X=xi)=64∗H(Y∣X=x(0−20))+61∗H(Y∣X=x(20−50))+61∗H(Y∣X=x(50−100))=32∗log2+2∗(−log1)=0.46209812037329684
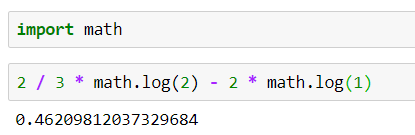
我们知道,熵是描述混乱程度的量,值越小说明其事件的确定性程度越高,所以应该是越小越好。所以我们,可以继续计算其余的特征值的条件熵,然后得出一个比较小的。
1.3 信息增益
但是,实际中在选择某个特征的时候,我们常使用的却是信息增益最大的那么特征。不妨看看信息增益的定义:
g
(
D
,
X
)
=
H
(
D
)
−
H
(
D
∣
X
)
g(D, X) = H(D) - H(D|X)
g(D,X)=H(D)−H(D∣X)
即,特征X在数据集D的信息增益,定义为数据集的熵减去特征X在数据集D下的条件熵。
在选取较好的特征的时候,我们需要计算这个数据集中的所有特征的信息增益,然后在比较这些特征下的信息增益即可。
2. 决策树
在上面我们知道了,使用信息增益可以帮助我们选择特征,以构建一颗决策树。那么思路就有了,也就是选择特征,然后构建一颗决策树,然后对于测试数据,就可以直接对比这棵树即可,就可以完成对未知数据的分类了。
按照惯例,这里给出原文的地址,here。以及数据集的下载地址。
数据集是这样一个文件:

2.1 熵计算
简单的数数,我们知道,这个数据集的交叉熵应该这样计算:

那么,不妨直接开始编写代码,不妨先定义一个计算数据集熵的函数,即:
# 计算数据集的熵值
def getEntropy(dataset):
_label_dict = dict()
for ele in dataset[:, -1]:
try:
_label_dict[ele] += 1
except:
_label_dict[ele] = 1
_sum = 0
for key in _label_dict.keys():
_prob = _label_dict[key] / len(dataset)
_sum += _prob * math.log(_prob)
return -1 * _sum
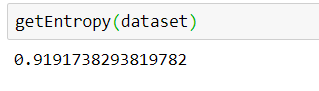
说明,我们计算数据集的熵的函数定义是没有问题的。
2.2 条件熵计算
那么,不妨简单的来定义下,计算条件熵,这里我们针对的特征列是第一列,如下:
第一列分3个类别,分别是:
category_1 = 8
category_2 = 8
category_3 = 8
对应的概率,分别是:
p_1 = 8 / 24
p_2 = 8 / 24
p_3 = 8 / 24
根据条件熵的计算公式,我们所求的为:
D_1 = 数据集前8行,表示为D[:8],同理,
D_2 = D[8:16]
D_3 = D[16:]
p_1 * H(D[:8]) + p_2 * H(D[8:16]) + p_3 * H(D[16:])
用这里定义好的计算数据集的条件熵的函数来表示,就是:
p_1 * getEntropy(dataset[:8]) + p_1 * getEntropy(dataset[8:16])
+ p_3 * getEntropy(dataset[16:])
那么,即:

所以,我们可以将之定义为一个函数,然后自己去计算这个所给特征列的条件熵,如下:
# 计算条件熵
def getConditionalEntropy(dataset, column):
# 1. 将指定特征列的特征分类,统计,然后计算概率
column_feature = dict()
for ele in dataset[:, column]:
try:
column_feature[ele] += 1
except:
column_feature[ele] = 1
print(column_feature)
# 2. 按照类别进行遍历,然后计算该子类别的分类的概率p
_sum = 0
for key in column_feature.keys():
# 当前类别的概率值
current_category_p = column_feature[key] / len(dataset)
# 遍历查找当前类别的所有元素,然后计算这个子数据集的熵
current_category_element_index = []
for _, ele in enumerate(dataset):
if ele[column] == key:
current_category_element_index.append(_)
sub_dataset = dataset[current_category_element_index, :]
_sum += current_category_p * getEntropy(sub_dataset)
return _sum
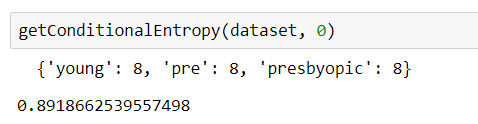
说明,我们的条件熵的计算也没有问题。
2.3 互信息计算
def get_most_max_index(_list):
# 下标数组
_index = list(range(len(_list)))
# 直接排序即可
for i in range(len(_list)):
for j in range(i+1, len(_list)):
if _list[i] > _list[j]:
# 元素
temp = _list[i]
_list[i] = _list[j]
_list[j] = temp
# 下标
temp = _index[i]
_index[i] = _index[j]
_index[j] = temp
return _index[-1], _index
def get_information_gains(dataset):
information_gains = []
# 待计算的特征下标
feature_indexs = list(range(len(dataset[0]) - 1))
dataset_entropy = getEntropy(dataset)
for feature_index in feature_indexs:
information_gain = dataset_entropy - getConditionalEntropy(dataset, feature_index)
information_gains.append(information_gain)
print(information_gains)
index, sorted_list = get_most_max_index(information_gains)
print("最优的特征的下标:", index)

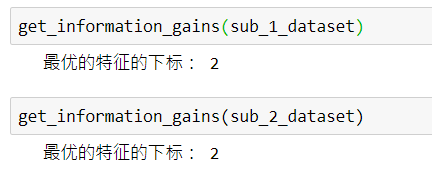
也就是,我们需要第四列的信贷情况作为我们的本次的最优特征。
然后,我们所需要的就是在计算机中构建这棵决策树了。不妨找找之前写的二叉树的代码,来借鉴下:
typedef int ElemType;
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild;
}*BiTree, BiTNode;
void CreateBiTreePreOrder(BiTree &T){
ElemType data;
cin>>data;
if(data==-1){
T=NULL;
}else{
T = new BiTNode();//(BiTree)malloc(sizeof(BiTNode));
}
if(!T){
return;
}else{
T->data = data;
CreateBiTreePreOrder(T->lchild);
CreateBiTreePreOrder(T->rchild);
}
}
简单的说,也就是可以递归的分别创建左右子树,直到Done。
理下思路,也就是找到最优的特征,然后,根据这个特征,将数据集分为几个类别,然后在这个类别上分别计算,类似于这种方式进行,如下:
- 第一次划分

即,划分成这两个子数据集:
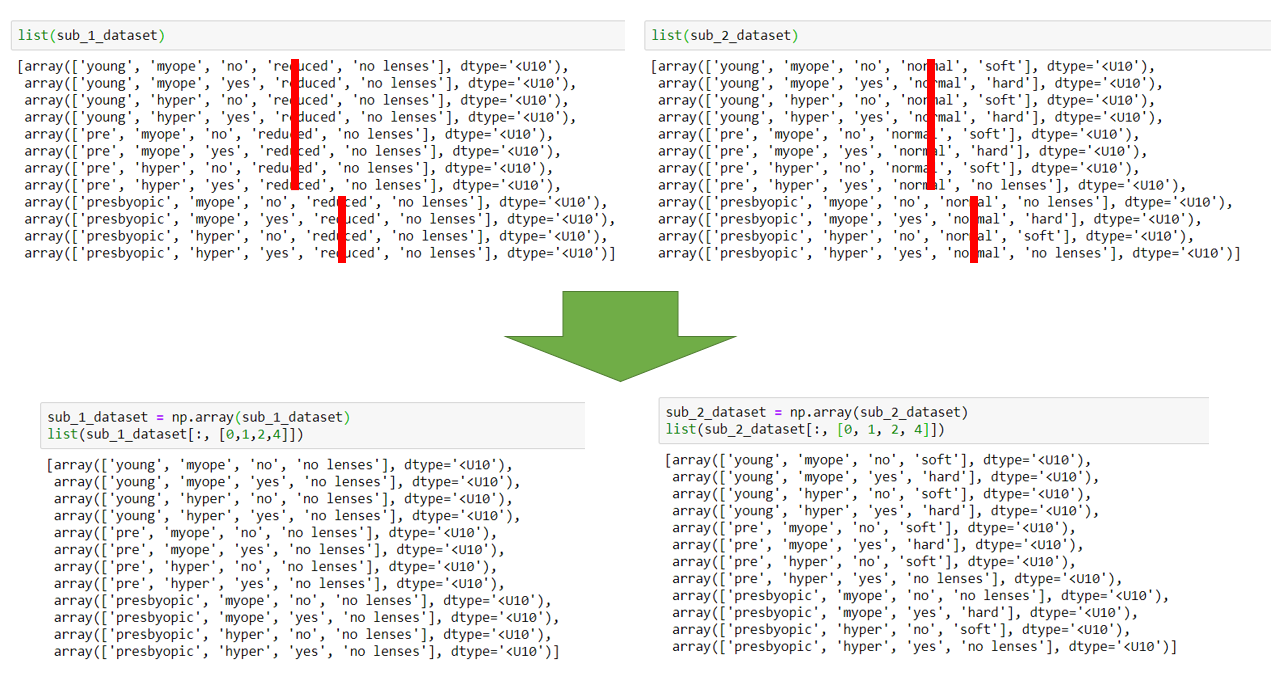
不妨对这两个子数据集,进行信息增益的计算,即:
那么,这棵树变成,:

然后,继续在划分的子数据集上,进行计算即可。
简单的写了下建立树的代码,这里直接给出完整代码:
import numpy as np
import math
# 获取数据
def getDataset(filename="lenses.txt"):
datas = []
with open(filename, mode="r", encoding="utf-8") as f:
lines = f.readlines()
for line in lines:
_line = line.split("t")
_line[4] = _line[4][:-1]
datas.append(_line)
return np.array(datas)
# 计算数据集的熵值
def getEntropy(dataset):
_label_dict = dict()
for ele in dataset[:, -1]:
try:
_label_dict[ele] += 1
except:
_label_dict[ele] = 1
_sum = 0
for key in _label_dict.keys():
_prob = _label_dict[key] / len(dataset)
_sum += _prob * math.log(_prob)
return -1 * _sum
# 计算条件熵
def getConditionalEntropy(dataset, column):
# 1. 将指定特征列的特征分类,统计,然后计算概率
column_feature = dict()
for ele in dataset[:, column]:
try:
column_feature[ele] += 1
except:
column_feature[ele] = 1
# 2. 按照类别进行遍历,然后计算该子类别的分类的概率p
_sum = 0
for key in column_feature.keys():
# 当前类别的概率值
current_category_p = column_feature[key] / len(dataset)
# 遍历查找当前类别的所有元素,然后计算这个子数据集的熵
current_category_element_index = []
for _, ele in enumerate(dataset):
if ele[column] == key:
current_category_element_index.append(_)
sub_dataset = dataset[current_category_element_index, :]
_sum += current_category_p * getEntropy(sub_dataset)
return _sum
def get_most_max_index(_list):
# 下标数组
_index = list(range(len(_list)))
# 直接排序即可
for i in range(len(_list)):
for j in range(i+1, len(_list)):
if _list[i] > _list[j]:
# 元素
temp = _list[i]
_list[i] = _list[j]
_list[j] = temp
# 下标
temp = _index[i]
_index[i] = _index[j]
_index[j] = temp
return _index[-1], _index
def get_information_gains(dataset):
information_gains = []
# 待计算的特征下标
feature_indexs = list(range(len(dataset[0]) - 1))
dataset_entropy = getEntropy(dataset)
for feature_index in feature_indexs:
information_gain = dataset_entropy - getConditionalEntropy(dataset, feature_index)
information_gains.append(information_gain)
index, sorted_list = get_most_max_index(information_gains)
return index
# 递归建立
def createTree(dataset, clomn_names, _tree = dict()):
if len(dataset) <= 1:
_tree[clomn_names[0]] = dataset[0][0]
return
else:
best_index = get_information_gains(dataset)
_tree[clomn_names[best_index]] = {}
best_clomn_options = set(list(dataset[:, best_index]))
for option in best_clomn_options:
_tree[clomn_names[best_index]][option] = {}
sub_dataset = []
for row in dataset:
if row[best_index] == option:
sub_dataset.append(list(row))
sub_dataset = np.array(sub_dataset)
clomn_indexs = list(range(len(clomn_names)))
clomn_indexs.remove(clomn_indexs[best_index])
sub_dataset = sub_dataset[:, clomn_indexs]
temp_clomn_names = clomn_names.copy()
temp_clomn_names.remove(temp_clomn_names[best_index])
createTree(sub_dataset, temp_clomn_names, _tree[clomn_names[best_index]][option])
clomn_names = ["年龄", "有工作", "有自己的房子", "信贷情况", "是否个给贷款"]
dataset = getDataset()
tree = {}
createTree(dataset, clomn_names, tree)
最后,查看下结果:

最后
以上就是独特乌冬面最近收集整理的关于决策树(一)的全部内容,更多相关决策树(一)内容请搜索靠谱客的其他文章。








发表评论 取消回复