基本概念
- 树状结构,可以很好的对数据进行分类
- 决策树的根节点到叶节点的每一条路径构建一条规则
- 具有互斥且完备的特点,即每一个样本均被且只能被一条路径所覆盖
- 只要提供的数据量足够庞大真实,通过数据挖掘模式,就可以构造决策树
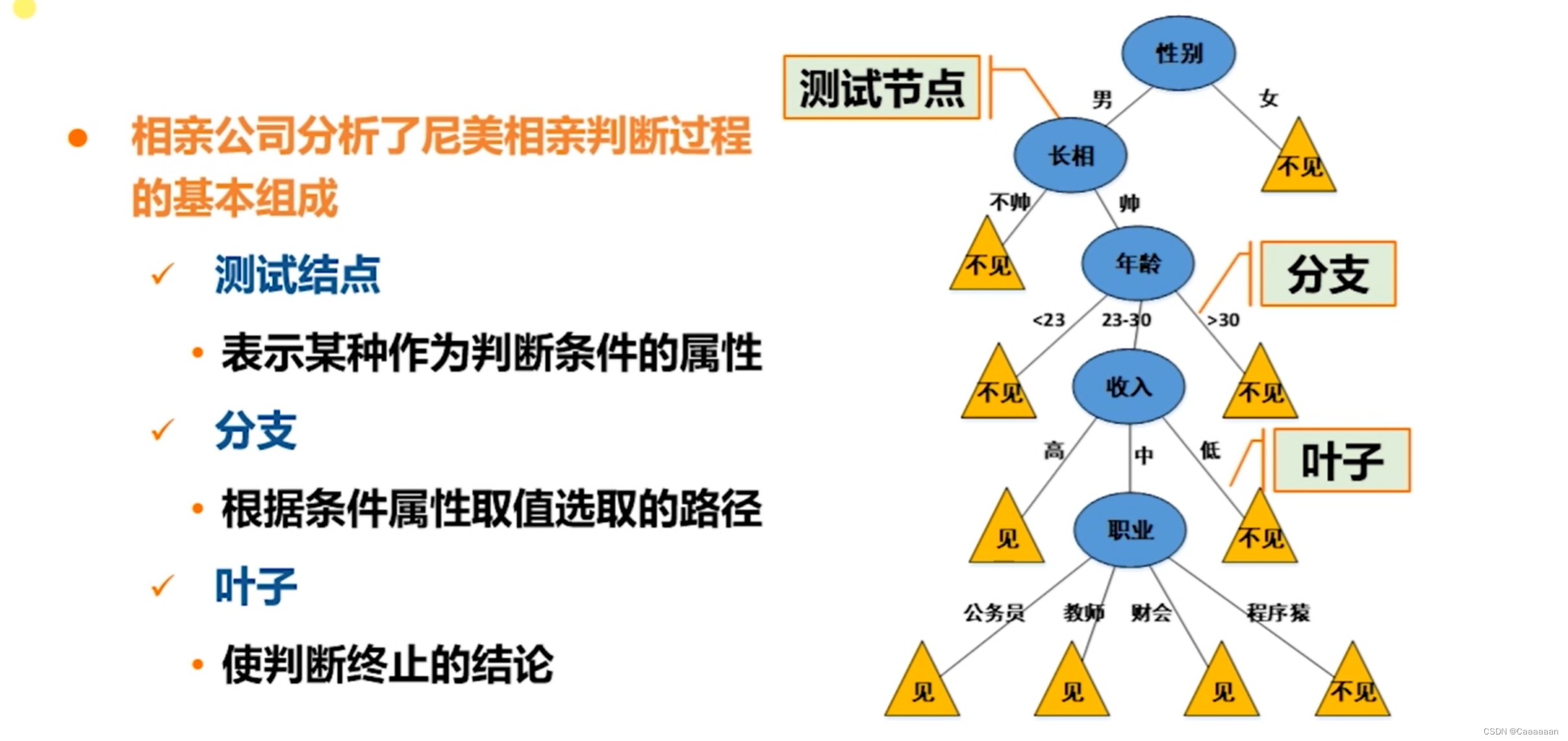
当决策属性的顺序不同时,就可以构建出不同的决策树
那么,哪种决策顺序是最好的
决策树构建
- 决策树归纳的设计问题
- 如何分裂训练记录
- 怎样为不同类型的属性指定测试条件
- 怎样评估每种测试条件
- 如何停止分裂过程
- 如何分裂训练记录
指定测试条件
要点一:属性的类型
- 标称、序数、连续
要点二:划分的路数
- 多路划分
- 二元划分
基于标称属性的分裂
-
多路划分:划分数(输出数)取决于该属性不同属性值的个数
例如:婚姻状态可以划分为 未婚、已婚、离婚
-
二元划分:划分数为2,这种划分需要考虑创建K个属性值的二元化分的所有有 2 k − 1 − 1 2^{k-1}-1 2k−1−1中方法
例如:婚姻状态划分为 {已婚,未婚}和{离婚}两类
或者:划分为{已婚,离婚}和{未婚}两类
基于序数属性的分裂
-
多路划分:划分数(输出数)取决于该属性不同属性值的个数
例如:把规模划分为 小、中、大
-
二元划分:划分数为2,这种划分需要考虑创建K个属性值的二元化分的所有有 2 k − 1 − 1 2^{k-1}-1 2k−1−1中方法
注意:对序数属性的分裂,要保留序数的有序性
即我们可以划分为{小,中}和{大} 或者 {小}和{中,大}
不能划分为{小,大}和{中}
基于连续属性的划分
-
二元划分:(A<v) or (A>=v)
考虑所有的划分点,选择一个最优划分点v
-
多路划分: v i ≤ A < v i + 1 ( i = 1 , . . . , k ) v_ileq A<v_{i+1}(i=1,...,k) vi≤A<vi+1(i=1,...,k)
即将连续数据离散化——等宽法,等频法,聚类等
评估测试条件
最佳划分
-
选择最佳划分的度量通常是根据划分后子结点纯性的程度
纯性的程度越高,类分布就越倾斜,划分结果就越好

Entropy基于熵
E n t r o p y ( s ) = − ∑ i = 1 C p i l o g ( p i ) p i 是数据属于第 i 个类别的概率 Entropy(s)=-sum_{i=1}^Cp_ilog(p_i)\ p_i是数据属于第i个类别的概率 Entropy(s)=−i=1∑Cpilog(pi)pi是数据属于第i个类别的概率
-
信息熵——
熵值是用来衡量数据的不确定性的一个数学的度量方法
-
熵值越高,数据越混乱
-
熵值越低,数据越纯
| c1 | 0 |
|---|---|
| c2 | 6 |
- 数据纯度高
E n t r o p y ( t ) = − ∑ j p ( j ∣ t ) l o g ( p ( j ∣ t ) ) p ( C 1 ) = 0 / 6 = 0 p ( C 2 ) = 6 / 6 = 1 E n t r o p y = − 0 l o g 0 − 1 l o g 1 = − 0 − 0 = 0 Entropy(t)=-sum_jp(j|t),log(p(j|t))\ p(C1)=0/6=0\ p(C2)=6/6=1\ Entropy=-0log0-1log1=-0-0=0\ Entropy(t)=−j∑p(j∣t)log(p(j∣t))p(C1)=0/6=0p(C2)=6/6=1Entropy=−0log0−1log1=−0−0=0

| C1 | 3 |
|---|---|
| C2 | 3 |
- 数据混乱
E n t r o p y ( t ) = − ∑ j p ( j ∣ t ) l o g ( p ( j ∣ t ) ) p ( C 1 ) = 3 / 6 = 1 / 2 p ( C 2 ) = 3 / 6 = 1 / 2 E n t r o p y = − 0.5 l o g 0.5 − 0.5 l o g 0.5 = 1 Entropy(t)=-sum_jp(j|t),log(p(j|t))\ p(C1)=3/6=1/2\ p(C2)=3/6=1/2\ Entropy=-0.5log0.5-0.5log0.5=1\ Entropy(t)=−j∑p(j∣t)log(p(j∣t))p(C1)=3/6=1/2p(C2)=3/6=1/2Entropy=−0.5log0.5−0.5log0.5=1
Hunt算法
设 D t D_t Dt是与节点t相关联的训练记录集,算法步骤如下:
- 如果 D t D_t Dt中所有的记录都属于同一个类 y t y_t yt,则t是叶节点,用 y t y_t yt标记
- 如果 D t D_t Dt中包含属于多个类的记录,则选择一个属性测试条件,将记录划分成较小的子集
- 对于测试条件的每个输出,创建一个子结点,并根据测试结果将 D t D_t Dt中的记录分布到子结点中。然后对于每个子结点,递归地调用该算法

-
我们先把具有还贷能力的记录拿出来,发现类标签都是No
即对应第一点, D t D_t Dt中的记录都属于同一类
-
然后,不具备还贷能力的,属于多个类的记录,因此选择一个属性测试条件——婚姻状况
然后发现,已经结婚的都是No,则结婚伸出来的是叶节点(有对应标签)
-
再在剩余的记录里,发现新的属性测试条件——收入情况
大于80k的都会做欺诈
(这个数值分类限定,可以通过回归或其他一些方式获得这个类别的界限)

算法特点
-
Hunt算法采用贪心策略构建决策树
在选择划分数据的属性是,采取一系列局部最优决策来构造决策树
信息增益算法ID3
基于Entropy基于熵
-
我们先不考虑任何一个特征,只考虑类标签,获得类标签的一个熵值
得到我们本身类标签是混乱的
E n t r o p y ( s ) = − 9 14 l o g 2 9 14 − 5 14 l o g 2 5 14 = 0.940 Entropy(s)=-frac{9}{14}log_2frac{9}{14}-frac{5}{14}log_2frac{5}{14}=0.940 Entropy(s)=−149log2149−145log2145=0.940

- 我通过选取的特征属性,将数据进行一个划分,观测熵值会不会发生变化
G a i n ( S , A ) = E n t r o p y ( S ) − ∑ v ∈ A ∣ S v ∣ ∣ S ∣ E n t r o p y ( S v ) ∙ 原始数据分类所需的期望信息 I n f o ( D ) = I ( 9 , 5 ) = − 9 14 l o g 2 9 14 − 5 14 l o g 2 5 14 = 0.940 ∙ 按照年龄分类所需的期望信息 期望信息 = 老年人占比 ∗ 老年人数据的信息熵 + 中年人占比 . . . I n f o a g e ( D ) = 5 14 I ( 2 , 3 ) + 4 14 I ( 0 , 4 ) + 5 14 I ( 3 , 2 ) = 5 14 ( − 2 5 l o g 2 2 5 − 3 5 l o g 2 3 5 ) + 4 14 ( − 0 4 l o g 2 0 4 − 4 4 l o g 2 4 4 ) + 5 14 ( − 3 5 l o g 2 3 5 − 2 5 l o g 2 2 5 ) = 0.694 Gain(S,A)=Entropy(S)-sum_{vin A}frac{|S_v|}{|S|}Entropy(S_v)\ bullet 原始数据分类所需的期望信息\ Info(D)=I(9,5)=-frac{9}{14}log_2frac{9}{14}-frac{5}{14}log_2frac{5}{14}=0.940\ bullet 按照年龄分类所需的期望信息\ 期望信息=老年人占比*老年人数据的信息熵+中年人占比...\ Info_{age}(D)=frac{5}{14}I(2,3)+frac{4}{14}I(0,4)+frac{5}{14}I(3,2)\ =frac{5}{14}(-frac{2}{5}log_2frac{2}{5}-frac{3}{5}log_2frac{3}{5})+\frac{4}{14}(-frac{0}{4}log_2frac{0}{4}-frac{4}{4}log_2frac{4}{4})+frac{5}{14}(-frac{3}{5}log_2frac{3}{5}-frac{2}{5}log_2frac{2}{5})\ =0.694 Gain(S,A)=Entropy(S)−v∈A∑∣S∣∣Sv∣Entropy(Sv)∙原始数据分类所需的期望信息Info(D)=I(9,5)=−149log2149−145log2145=0.940∙按照年龄分类所需的期望信息期望信息=老年人占比∗老年人数据的信息熵+中年人占比...Infoage(D)=145I(2,3)+144I(0,4)+145I(3,2)=145(−52log252−53log253)+144(−40log240−44log244)+145(−53log253−52log252)=0.694
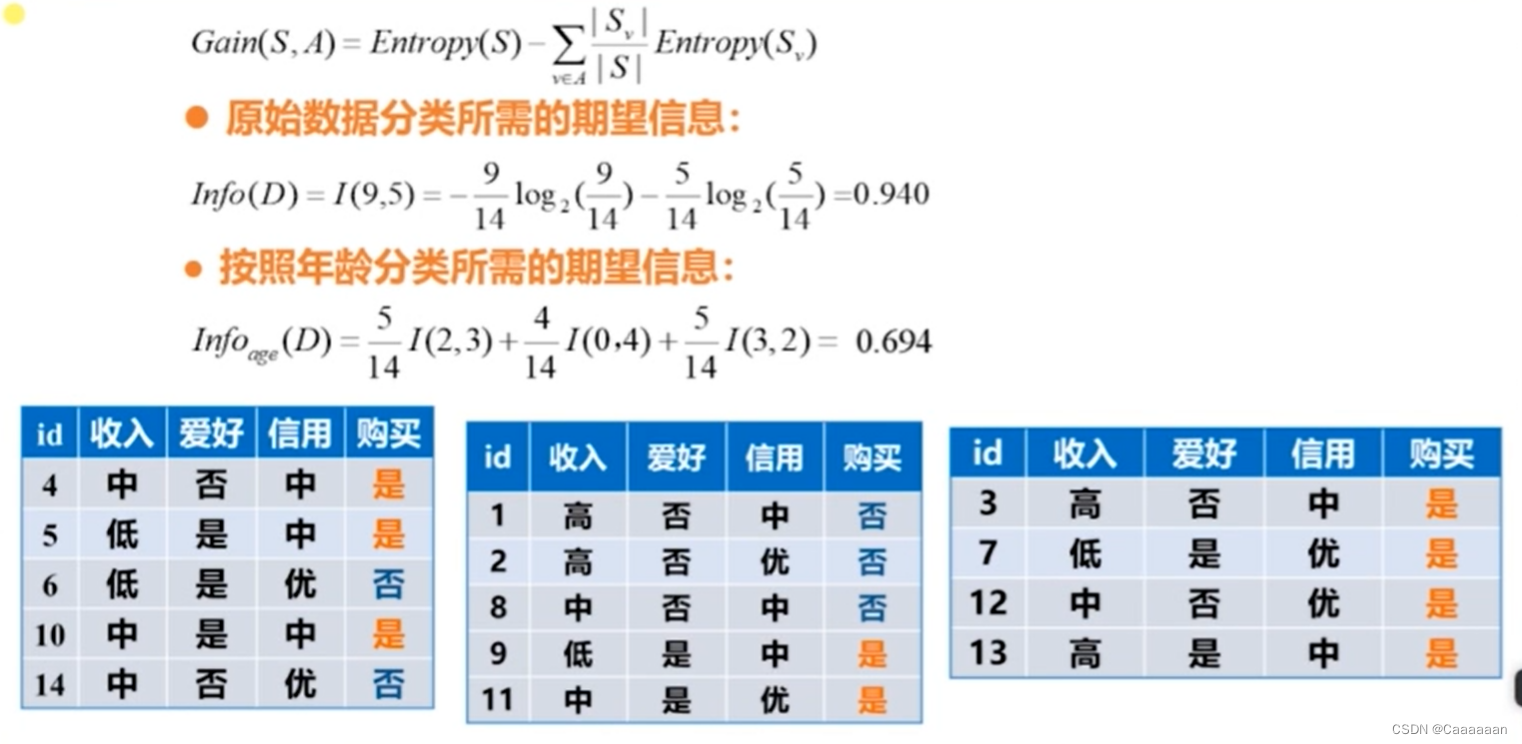
- 则按照年龄来划分,使得数据信息熵降低为了0.694
所谓信息增益Gain,就是原本的信息熵-划分之后的信息熵
即,在本次示例中,按照年龄分类所带来的信息熵是0.94-0.694=0.246
同理,我们得到
-
G a i n ( a g e ) = 0.246 Gain(age)=0.246 Gain(age)=0.246
-
G a i n ( i n c o m e ) = 0.029 Gain(income)=0.029 Gain(income)=0.029
-
G a i n ( f a n c y ) = 0.151 Gain(fancy)=0.151 Gain(fancy)=0.151
-
G a i n ( c r e d i t _ r a t i n g ) = 0.048 Gain(credit_rating)=0.048 Gain(credit_rating)=0.048
-
在信息增益算法ID3里面,我们通过信息增益最大的属性,作为根节点
-
信息增益从大到小,决策树从上到下,递归构造
-
直到数据都属于同一类,分裂停止
算法特点
- 要求数据都是离散的(才可以计算概率和信息熵)
计算纯度扩展
除了上述提及的Entropy信息熵,还有Gini指数和分类误差
GINI指数
给点结点 t 的 G i n i 值计算: G I N I ( t ) = 1 − ∑ j [ p ( j ∣ t ) ] 2 p ( j ∣ t ) 是在结点 t 中,类 j 发生的概率 给点结点t的Gini值计算:\ GINI(t)=1-sum_j[p(j|t)]^2\ p(j|t)是在结点t中,类j发生的概率 给点结点t的Gini值计算:GINI(t)=1−j∑[p(j∣t)]2p(j∣t)是在结点t中,类j发生的概率
- 当类分布均衡时,GINI值达到最大值
- 相反,当只有一个类时,GINI值达到最小值0,纯性越大
- GINI指数不需要计算对数,一定程度上可以降低计算开销
Classification Error
给点结点 t 的 C l a s s i f i c a t i o n E r r o r 值计算: E r r o r ( t ) = 1 − m a x P ( i ∣ t ) 给点结点t的Classification Error值计算:\ Error(t)=1-maxP(i|t)\ 给点结点t的ClassificationError值计算:Error(t)=1−maxP(i∣t)
- 当类分布均衡时,分类错误值达到最大
- 只有一个类时,分类错误值达到最小值0,纯性越大
连续变量处理
分割区间策略

- 对其进行一个排序,按照等宽法进行分类——即离散化

得到离散区间——收入高、收入中等、收入低
-
排序,然后从最小值开始建立分割区间,开始计算各自的信息增益
选择信息增益最大的一个分割区间作为最佳划分点
得到一个二路划分

分类案例
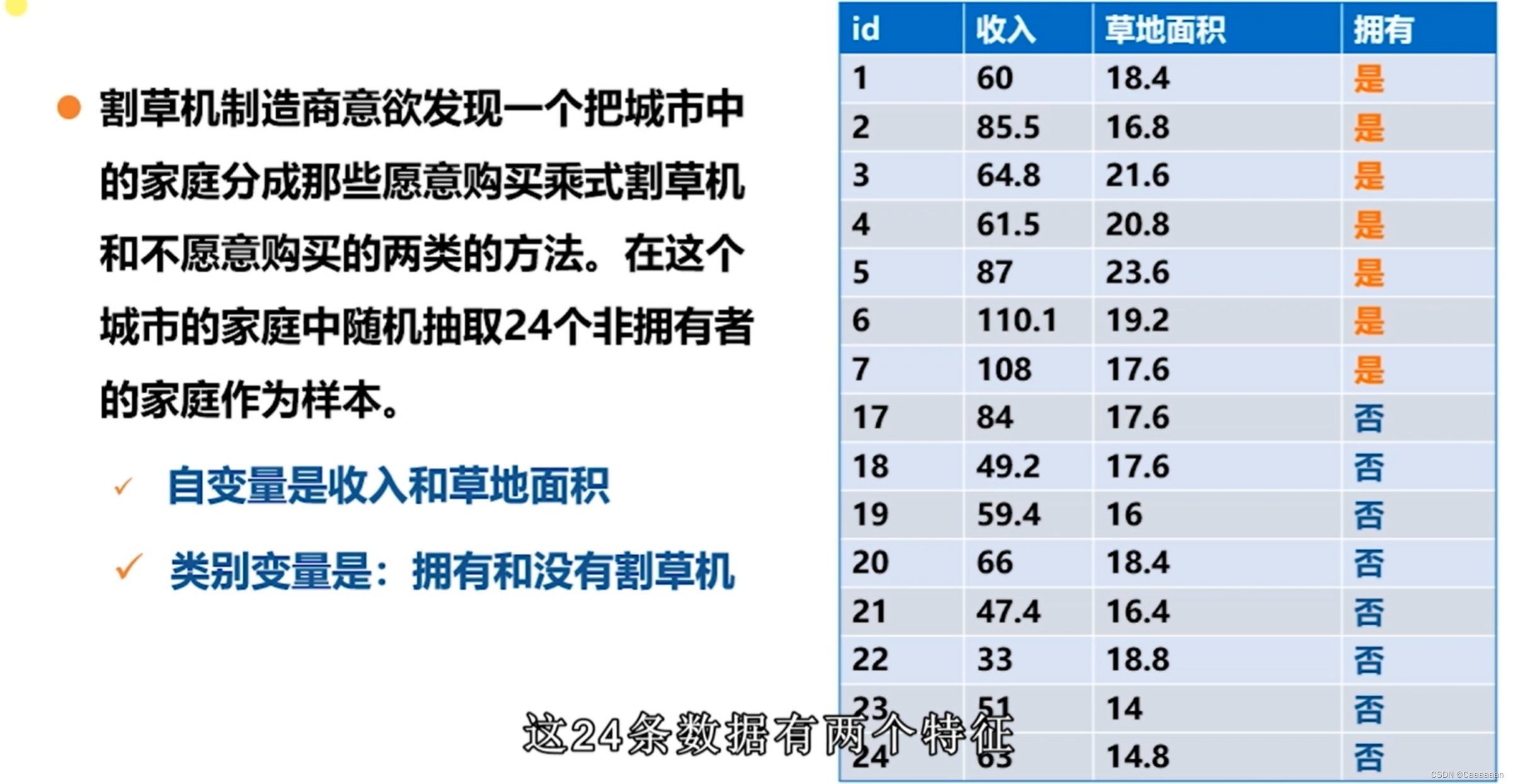
对应的特征都是连续变量
- 排序
- 选择某特征,寻找使得信息增益最大的分裂点
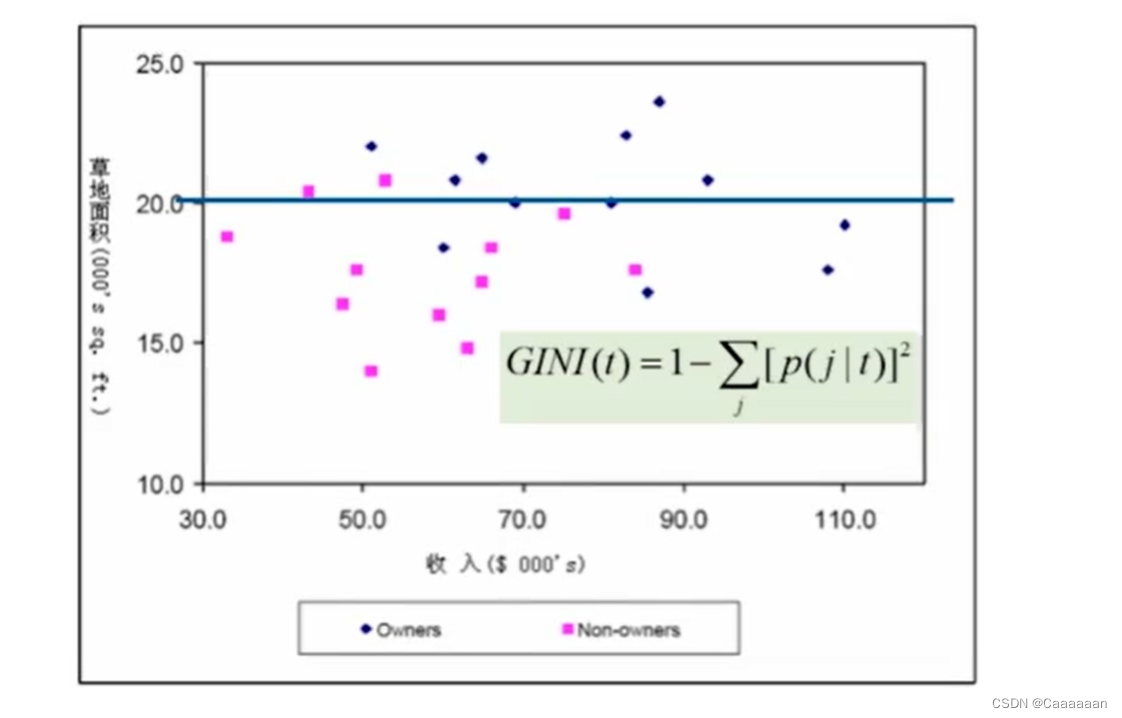
——图为根据草地面积寻找信息增益最大的分裂点
- 递归寻找,每一类里的属性差别
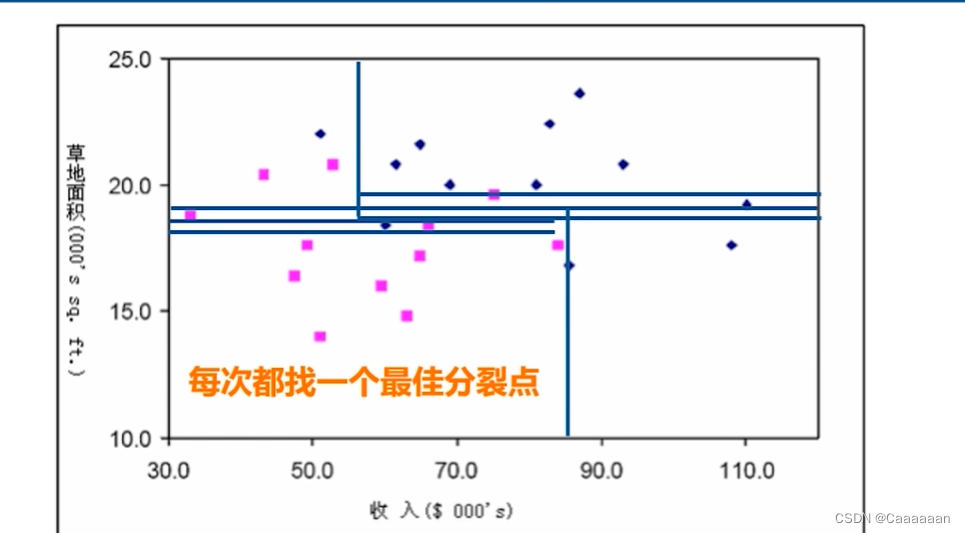
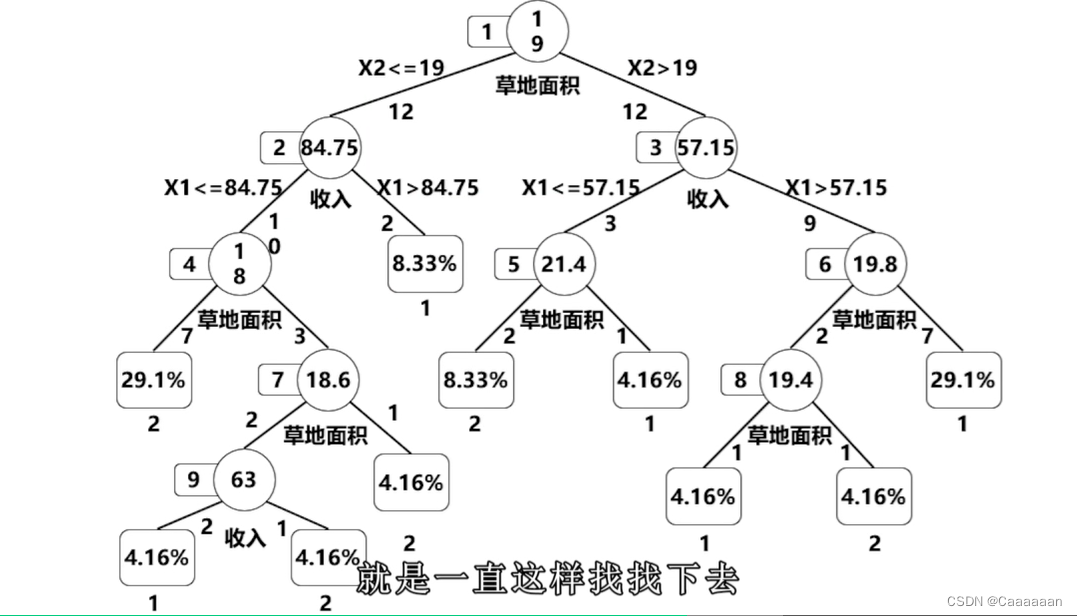
- 如此的过程是通过CART算法进行,本质上运用的是GINI指数
过拟合问题
- 复杂的决策时容易带来过拟合问题
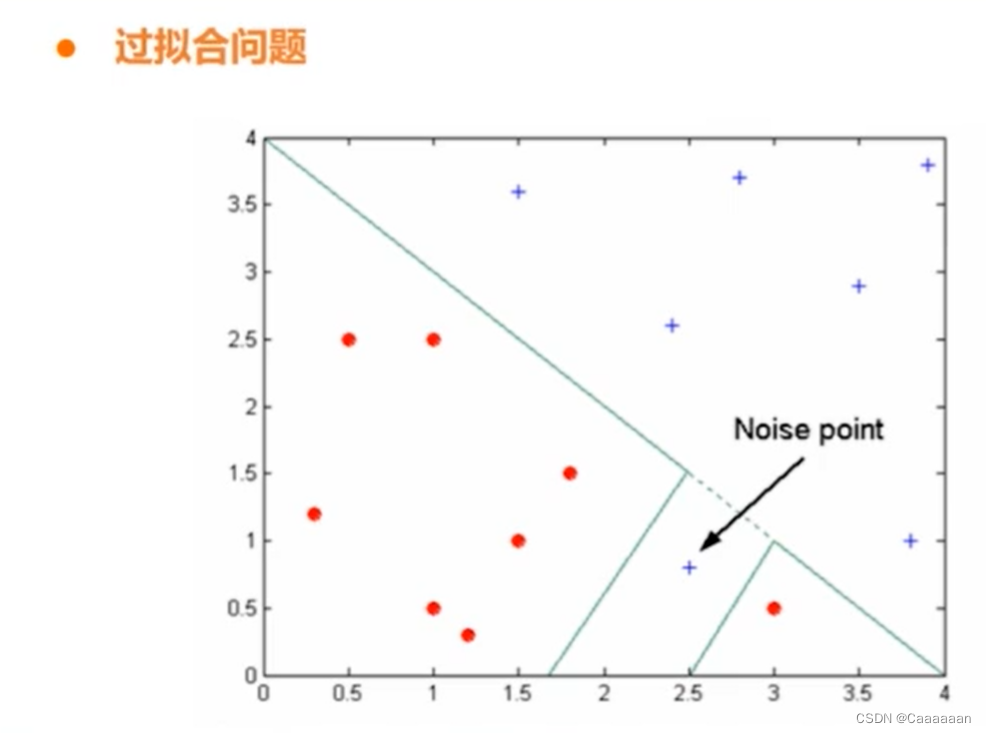
- 从图中可以看出,这个蓝点其实是个噪音点
- 但决策树的思路下,我们会在其附近划分出一片空间,认为是属于蓝色
- 但实质上,那片空间的点也应该属于红圈
- 这就叫做过拟合

剪枝方法
为了避免决策树过于复杂,我们通过剪枝才避免过拟合情况的发生
-
Prepruning:如果划分带来的信息增益、Gini指标等低于阈值或元组数目低于阈值,则停止这次划分
-
Postpruning:从完全生长的树中剪去树枝——得到一个逐步修剪树
度量分类器性能
事后剪枝,使用新的测试及,将错误率比较高的分支给删掉
-
过拟合是由于训练集少,模型过于复杂
-
欠拟合是由于训练集多,模型过于简单
决策树特点
-
决策树是一种构建分类模型的非参数方法
不像深度学习和神经网络,需要估算w权值
-
不需要昂贵的计算代价
只需要计算信息熵,信息增益等
-
决策树相对容易解释
-
决策树是学习离散值函数的典型代表
-
决策树对于噪声的干扰具有相当好的鲁棒性
通过事前剪枝或事后剪枝,将噪音点去除
-
冗余属性不会对决策树的准确率造成不利影响
因为决策树本质是,通过信息增益,优先选择最能够划分类别的属性
同时,冗余属性可能因为事前剪枝阈值的设定,压根不会进行考虑
-
决策时无法学习特征之间的线性关系:特征构造
最后
以上就是帅气摩托最近收集整理的关于分类之决策树分类基本概念决策树构建分类案例决策树特点的全部内容,更多相关分类之决策树分类基本概念决策树构建分类案例决策树特点内容请搜索靠谱客的其他文章。








发表评论 取消回复