机器学习——决策树

在现实生活中，我们会遇到各种选择，不论是选择男女朋友，还是挑选水果，都是基于以往的经验来做判断。如果把判断背后的逻辑整理成一个结构图，你会发现它实际上是一个树状图，这就是我们今天要讲的决策树。

决策树的工作原理

决策树基本上就是把我们以前的经验总结出来。如果我们要出门打篮球，一般会根据“天气”、“温度”、“湿度”、“刮风”这几个条件来判断，最后得到结果：去打篮球？还是不去？

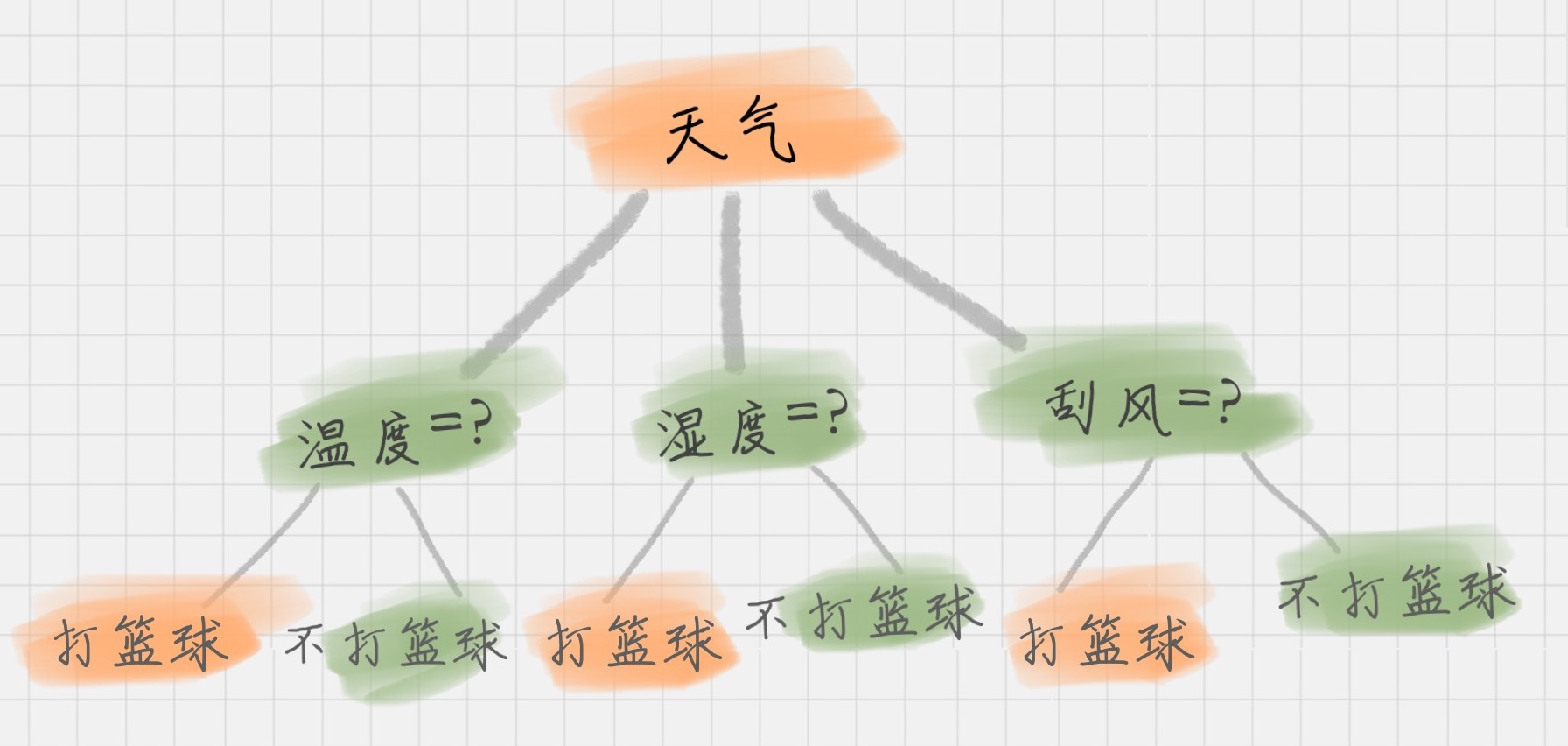
上面这个图就是一棵典型的决策树。我们在做决策树的时候，会经历两个阶段：构造和剪枝。

构造

构造就是生成一棵完整的决策树。简单来说，构造的过程就是选择什么属性作为节点的过程，那么在构造过程中，会存在三种节点：

1. 根节点：就是树的最顶端，最开始的那个节点。在上图中，“天气”就是一个根节点；
2. 内部节点：就是树中间的那些节点，比如说“温度”、“湿度”、“刮风”；
3. 叶子节点：就是树最底部的节点，也就是决策结果。

节点之间存在父子关系。比如根节点会有子节点，子节点会有子子节点，但是到了叶子节点就停止了，叶子节点不存在子节点。那么在构造过程中，你要解决三个重要的问题：

1. 选择哪个属性作为根节点；
2. 选择哪些属性作为子节点；
3. 什么时候停止并得到目标状态，即叶子节点。

剪枝

剪枝就是给决策树瘦身，这一步想实现的目标就是，不需要太多的判断，同样可以得到不错的结果。之所以这么做，是为了防止“过拟合”（Overfitting）现象的发生。

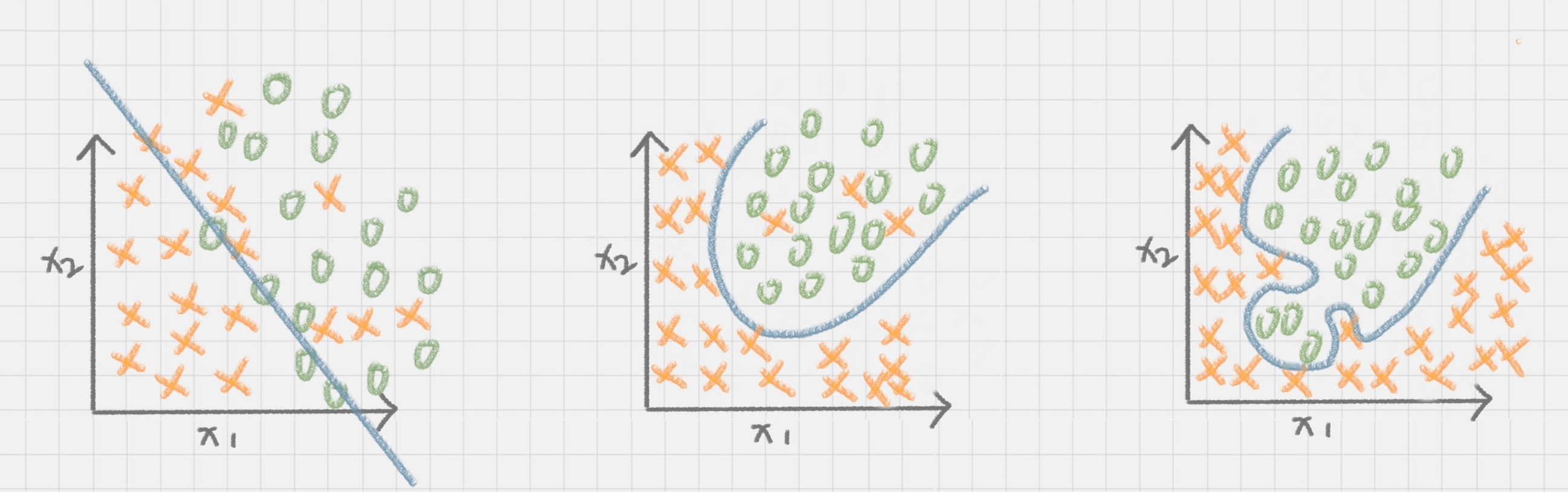
造成过拟合的原因：

一是因为训练集中样本量较小。如果决策树选择的属性过多，构造出来的决策树一定能够“完美”地把训练集中的样本分类，但是这样就会把训练集中一些数据的特点当成所有数据的特点，但这个特点不一定是全部数据的特点，这就使得这个决策树在真实的数据分类中出现错误，也就是模型的“泛化能力”差。

泛化能力：

指的分类器是通过训练集抽象出来的分类能力，你也可以理解是举一反三的能力。如果我们太依赖于训练集的数据，那么得到的决策树容错率就会比较低，泛化能力差。因为训练集只是全部数据的抽样，并不能体现全部数据的特点。

剪枝的方法：

• 预剪枝：在决策树构造时就进行剪枝。方法是，在构造的过程中对节点进行评估，如果对某个节点进行划分，在验证集中不能带来准确性的提升，那么对这个节点进行划分就没有意义，这时就会把当前节点作为叶节点，不对其进行划分。
• 后剪枝：在生成决策树之后再进行剪枝。通常会从决策树的叶节点开始，逐层向上对每个节点进行评估。如果剪掉这个节点子树，与保留该节点子树在分类准确性上差别不大；或者剪掉该节点子树，能在验证集中带来准确性的提升，那么就可以把该节点子树进行剪枝。方法是：用这个节点子树的叶子节点来替代该节点，类标记为这个节点子树中最频繁的那个类。

如何判断要不要去打篮球？

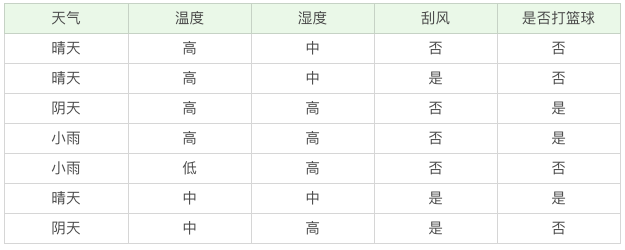
我们该如何构造一个判断是否去打篮球的决策树呢？再回顾一下决策树的构造原理，在决策过程中有三个重要的问题：将哪个属性作为根节点？选择哪些属性作为后继节点？什么时候停止并得到目标值？
显然将哪个属性（天气、温度、湿度、刮风）作为根节点是个关键问题，在这里我们先介绍两个指标：纯度和信息熵。

纯度

你可以把决策树的构造过程理解成为寻找纯净划分的过程。数学上，我们可以用纯度来表示，纯度换一种方式来解释就是让目标变量的分歧最小。
举个例子，假设有 3 个集合：

• 集合 1：6 次都去打篮球；
• 集合 2：4 次去打篮球，2 次不去打篮球；
• 集合 3：3 次去打篮球，3 次不去打篮球。

按照纯度指标来说，集合 1> 集合 2> 集合 3。因为集合1 的分歧最小，集合 3 的分歧最大。

信息熵

表示信息的不确定度。
在信息论中，随机离散事件出现的概率存在着不确定性。为了衡量这种信息的不确定性，信息学之父香农引入了信息熵的概念，并给出了计算信息熵的数学公式：$$Entropy(t)=-\Sigma p(i|t)lo{g}_{2}p(i|t)$$

p(i|t) 代表了i这一结果在条件t下出现的概率； $lo{g}_2$为取以 2 为底的对数。
这里我们并不详细介绍信息熵公式 ，而是说存在一种度量，它能帮我们反映出来这个信息的不确定度。当不确定性越大时，它所包含的信息量也就越大，信息熵也就越高。

举个例子，假设有 2 个集合：

• 集合 1：5 次去打篮球，1 次不去打篮球；
• 集合 2：3 次去打篮球，3 次不去打篮球。

在集合 1 中，有 6 次决策，其中打篮球是 5 次，不打篮球是 1 次。
那么在没有附加条件（即条件t为1–>全部，这里涉及到后续附加特征属性时，要做加权处理）的情况下，打篮球的概率是 5/6，不打篮球的概率是1/6，带入上述信息熵公式可以计算得出：$$Entropy(t)=-(5/6)lo{g}_2(5/6)-(1/6)lo{g}_2(1/6)=0.65$$

同样，集合 2 中，也是一共 6 次决策，打篮球与不打篮球的概率是3/6，那么信息熵为多少呢？我们可以计算得出：$$Entropy(t)=-(3/6)lo{g}_2(3/6)-(3/6)lo{g}_2(3/6)=1$$

从上面的计算结果中可以看出，信息熵越大，纯度越低。当集合中的所有样本均匀混合时，信息熵最大，纯度最低。

我们在构造决策树的时候，会基于纯度来构建。而经典的 “不纯度”的指标有三种，分别是：
信息增益（ID3 算法）、信息增益率（C4.5 算法） 以及 基尼指数（Cart 算法）。

1. ID3 算法：

信息增益指的就是划分可以带来纯度的提高，信息熵的下降。它的计算公式，是信息增益 = 划分前熵 - 划分后熵。在计算的过程中，我们会计算条件下每个分支的归一化信息熵，即用每个分支在该属性中出现的概率，来乘以该分支的信息熵。所以信息增益的公式可以表示为：
$$Gain(D,a)=Entropy(D)-\Sigma \frac{|D_i|}{|D|}Entropy(D_i)$$
Gain(D,a)中 D 是当前结点包含的所有结果（来自父节点某一分支）， a 是为划分这些结果所选的属性，Di 则是属性a下不同的分支所包含的结果

• 例如训练集中我们共有7组数据，其中3次结果是打篮球，4次是不打篮球
• 如果我们选择a = 刮风，即利用刮风来对这7次结果作进一步划分
• 那么D1为刮风 = 是，有 1 次打篮球，2 次不打篮球。
• 而D2为刮风 = 否，有 2 次打篮球，2 次不打篮球。

针对上例，D 节点以刮风为附加条件的信息增益为：
$$Gain(D,刮风)=Entropy(D)-(\frac{3}{7}Entropy(刮风=是)+\frac{4}{7}Entropy(刮风=否))$$
其中：

• $$Entropy(D)=-\frac{3}{7}lo{g}_2(\frac{3}{7})-\frac{4}{7}lo{g}_2(\frac{4}{7})\approx 0.985$$
• $$Entropy(刮风=是)=-\frac{1}{3}lo{g}_2(\frac{1}{3})-\frac{2}{3}lo{g}_2(\frac{2}{3})\approx 0.918$$
• $$Entropy(刮风=否)=-\frac{1}{2}lo{g}_2(\frac{1}{2})-\frac{1}{2}lo{g}_2(\frac{1}{2})=1$$

最终解得刮风作为节点属性时的节点增益：

• $$Gain(D,刮风)=0.985-(\frac{3}{7}\times 0.918+\frac{4}{7}\times 1)\approx 0.02$$

同理我们可以计算出其他属性作为节点属性时的信息增益，它们分别为：

• $$Gain(D,温度)=0.128$$
• $$Gain(D,湿度)=0.020$$
• $$Gain(D,天气)=0.020$$

我们能看出来温度作为属性的信息增益最大。因为 ID3 就是要选取信息增益最大属性作为节点，这样可以得到纯度高的决策树，所以我们将温度作为根节点。

我们在编号后用 + 代表去打篮球，- 代表不去打篮球，其决策树状图分裂为下图所示：

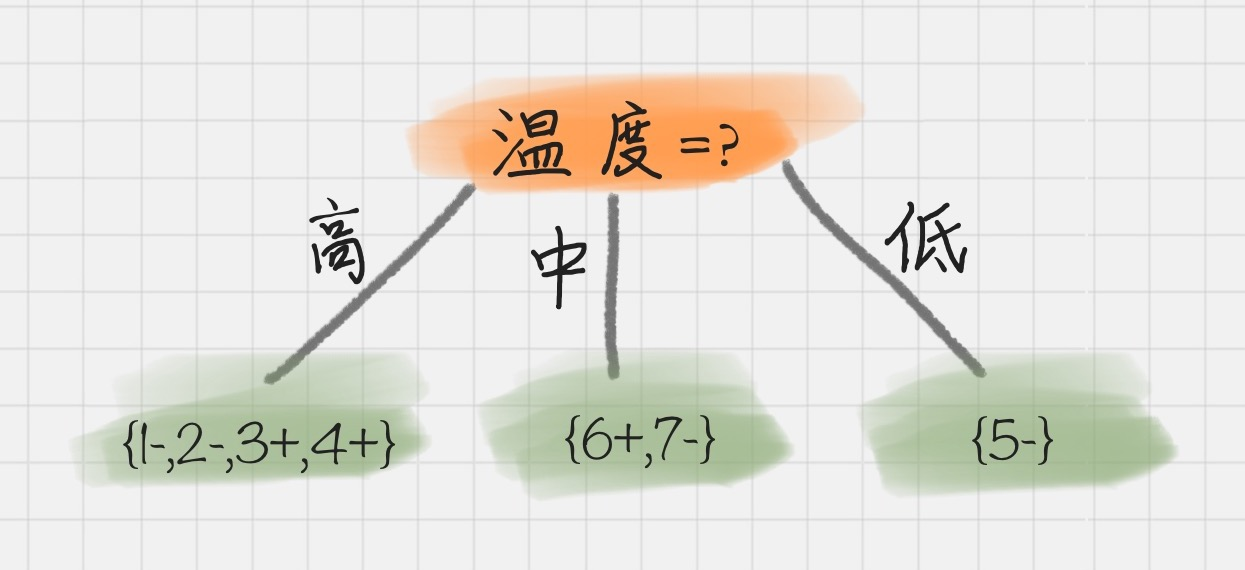
然后我们要对上图中每一个叶子节点再指定属性做进一步划分；
如对上图中第一个叶子节点，也就是 D1={1-,2-,3+,4+}做进一步划分，计算其不同属性（天气、湿度、刮风）作为节点属性时的信息增益，可以得到：

• $$Gain(D,天气)=0$$
• $$Gain(D,湿度)=0$$
• $$Gain(D,刮风)=0.0615$$

我们能看到刮风为 D1 的节点都可以得到最大的信息增益，这里我们选取刮风作为节点属性。
同理，我们再重复上面的计算步骤可以得到完整的决策树，结果如下：(晴天湿度为中，阴雨天湿度为高，湿度属性被天气属性覆盖了)

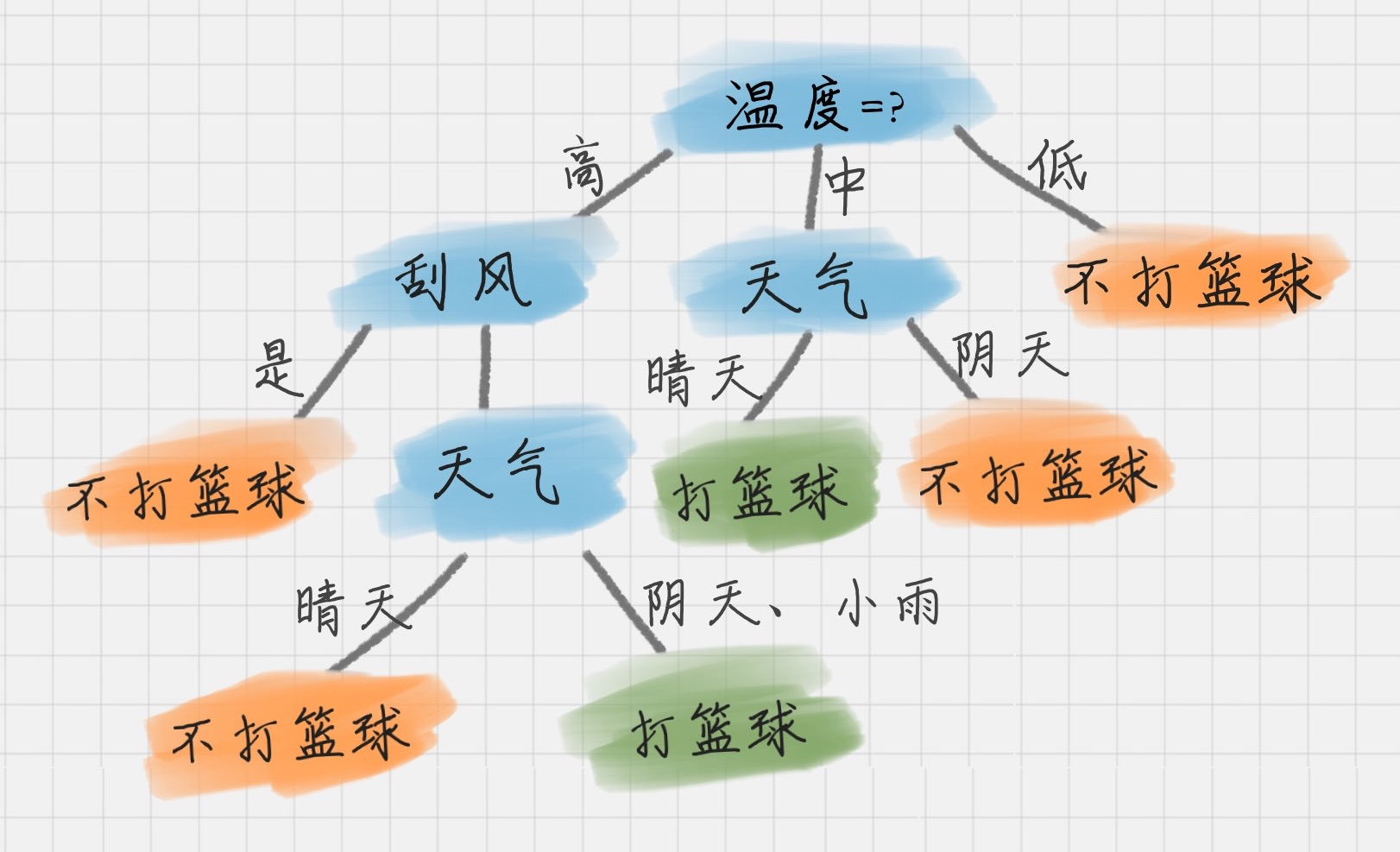
于是我们通过 ID3 算法得到了一棵决策树。ID3 的算法规则相对简单，可解释性强。同样也存在缺陷，比如我们会发现 ID3 算法倾向于选择取值（分支类别）比较多的属性。这是因为若分支增多，将导致其中每一个分支下对应的结果数量减少，从而可能提高某一结果出现的确定性，导致该分支的熵值较小，最终加权平均得到属性的熵值也很小；

• 例如我们把“编号”作为一个属性（一般情况下不会这么做，这里只是举个例子）；
• 由于编号中每一个取值都对应了一个确定的结果，所以当其作为节点属性时，每一个分支的熵值均为0，最终$\Sigma \frac{|D_i|}{|D|}Entropy(D_i)=0$，从而导致$Gain(D,编号)=1$，直接当选最优属性；
• 但实际上“编号”是无关属性的，它对“打篮球”的分类并没有太大作用。

所以 ID3 有一个缺陷就是，有些属性可能对分类任务没有太大作用，但是他们仍然可能会被选为最优属性。这种缺陷不是每次都会发生，只是存在一定的概率。在大部分情况下，ID3 都能生成不错的决策树分类。针对可能发生的缺陷，后人提出了新的算法进行改进。

2. C4.5 算法：

在 ID3 算法上进行了改进；

1）采用信息增益率：

因为 ID3 在计算的时候，倾向于选择取值多的属性。为了避免这个问题，C4.5 采用**信息增益率（也叫信息增益比）**的方式来选择属性。信息增益率 = 信息增益 / 所选属性信息熵。
当属性有很多值的时候，相当于被划分成了许多份，虽然信息增益变大了，但是对于 C4.5 来说，这个属性自身的信息熵 $Entropy(a)$ 也会变大，所以整体的信息增益率并不大。

我们来尝试计算一下各个属性的信息熵：

• $$Entropy(刮风)=-\frac{4}{7}lo{g}_2(\frac{4}{7})-\frac{3}{7}lo{g}_2(\frac{3}{7})=0.985$$
• $$Entropy(湿度)=-\frac{4}{7}lo{g}_2(\frac{4}{7})-\frac{3}{7}lo{g}_2(\frac{3}{7})=0.985$$
• $$Entropy(温度)=-\frac{4}{7}lo{g}_2(\frac{4}{7})-\frac{1}{7}lo{g}_2(\frac{1}{7})-\frac{2}{7}lo{g}_2(\frac{2}{7})=1.379$$
• $$Entropy(天气)=-\frac{3}{7}lo{g}_2(\frac{3}{7})-\frac{2}{7}lo{g}_2(\frac{2}{7})-\frac{2}{7}lo{g}_2(\frac{2}{7})=1.557$$

再根据各属性的信息增益Gain，可得信息增益比Gain ratio：

• $$Gai{n}_r(D,温度)=1.128÷1.379\approx 0.818$$
• $$Gai{n}_r(D,天气)=0.02÷1.557\approx 0.013$$
• $$Gai{n}_r(D,湿度)=0.02÷0.985\approx 0.020$$
• $$Gai{n}_r(D,刮风)=0.02÷0.985\approx 0.020$$

可以得到此时温度为最佳属性（温度存在一个分支的信息熵为1，影响较大，说明信息增益比也存在短板）

2）采用悲观剪枝：

ID3 构造决策树的时候，容易产生过拟合的情况。在 C4.5中，会在决策树构造之后采用悲观剪枝（PEP），这样可以提升决策树的泛化能力。

悲观剪枝是后剪枝技术中的一种，通过递归估算每个内部节点的分类错误率，比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝。这种剪枝方法不再需要一个单独的测试数据集。

3）离散化处理连续属性：

C4.5 可以处理连续属性的情况，对连续的属性进行离散化的处理。比如打篮球存在的“湿度”属性，不按照“高、中”划分，而是按照湿度值进行计算，那么湿度取什么值都有可能。该怎么选择这个阈值呢，C4.5 选择具有最高信息增益的划分所对应的阈值。

4）处理缺失值：

针对数据集不完整的情况，C4.5 也可以进行处理。

假如我们得到的是如下的数据，你会发现这个数据中存在两点问题：

• 第一个问题是，数据集中存在数值缺失的情况，如何进行属性选择？
• 第二个问题是，假设已经做了属性划分，但是样本在这个属性上有缺失值，该如何对样本进行划分？
  

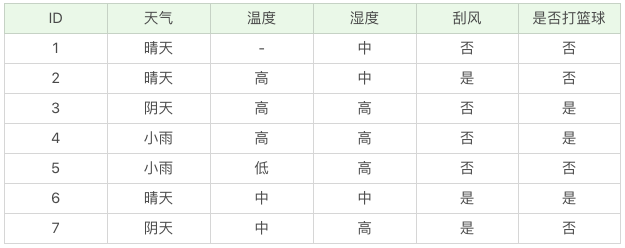
我们不考虑缺失的数值，可以得到：

• D’ = {2-,3+,4+,5-,6+,7-}，我们设 a=温度 则有：
• 温度 = 高：D1={2-,3+,4+}；
• 温度 = 中：D2={6+,7-}；
• 温度 = 低：D3={5-} 。

这里 + 号代表打篮球，- 号代表不打篮球。比如ID=2 时，决策是不打篮球，我们可以记录为 2-。

所以三个叶节点的信息熵可以结算为：

• $$Entropy(D1)=-\frac{1}{3}lo{g}_2(\frac{1}{3})-\frac{2}{3}lo{g}_2(\frac{2}{3})\approx 0.918$$
• $$Entropy(D2)=-\frac{1}{2}lo{g}_2(\frac{1}{2})-\frac{1}{2}lo{g}_2(\frac{1}{2})=1.0$$
• $$Entropy(D3)=0$$

这三个节点的归一化信息熵为：

• $$-\Sigma \frac{|D_i|}{|D^{\prime }|}Entropy(D_i)=-\frac{3}{6}\times 0.918+-\frac{2}{6}\times 1.0+-\frac{1}{6}\times 0=0.792$$

D’中共有3次去打篮球，3次不去打篮球，则：

• $$Entropy(D\prime )=-\frac{1}{2}lo{g}_2(\frac{1}{2})-\frac{1}{2}lo{g}_2(\frac{1}{2})=1.0$$

针对将属性选择为温度的信息增益为：

• $$Gain(D\prime ,温度)=Ent(D\prime )-0.792=1.0-0.792=0.208$$

D′的样本个数为 6，而 D 的样本个数为 7，所以无缺失值样本所占比例为 6/7，所以 Gain(D′，温度) 所占权重比例为6/7，所以：$$Gain(D,温度)=\frac{6}{7}\times 0.208+\frac{1}{7}\times 0=0.178$$

• 这样即使在温度属性的数值有缺失的情况下，我们依然可以计算信息增益，并对属性进行选择。

3. 比较总结：

• 信息熵表示的是数据中包含的信息量大小。信息熵越小，数据的纯度越高，也就是说数据越趋于一致（确定性强），这是我们希望的划分之后每个子节点的样子。
• 而信息增益 = 划分前熵 - 划分后熵，信息增益越大，则意味着使用属性 a 来进行划分所获得的 “纯度提升” 越大 ；也就是说，用属性 a 来划分训练集，得到的结果中纯度比较高。
• ID3 仅仅适用于二分类问题，ID3 仅仅能够处理离散属性。

本文转载自：https://www.cnblogs.com/molieren/articles/10664954.html
原作者文章中有一些小问题没说清的我做了处理，整个讲解的流程设计的很好????

最后

以上就是呆萌外套为你收集整理的机器学习方法——举例分析决策树机器学习——决策树的全部内容，希望文章能够帮你解决机器学习方法——举例分析决策树机器学习——决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。