决策树
- 什么是决策树
- 信息增益——熵,基尼指数
- 熵
- 基尼指数
- CART 算法模型实战
- 分类树
- 树的可视化
- 回归树
- 总结
什么是决策树
决策树是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果,类似于数据结构中的树。决策树是一个非常成熟的算法,最常用的三种决策树算法是ID3,C4.5,CART(Classification and Regression Tree)。这三种算法的区别是:ID3是利用信息增益来选择特征的。而C4.5,它是 ID3 的改进版,不是直接使用信息增益,而是引入“信息增益比”指标作为特征的选择依据。CART 算法是使用了基尼系数取代了信息熵来选择特征,它即可以用于分类,也可以用于回归问题,所以它的应用场景会比前两种算法更多。下面我们利用一棵CART二叉决策树来理解下决策树。
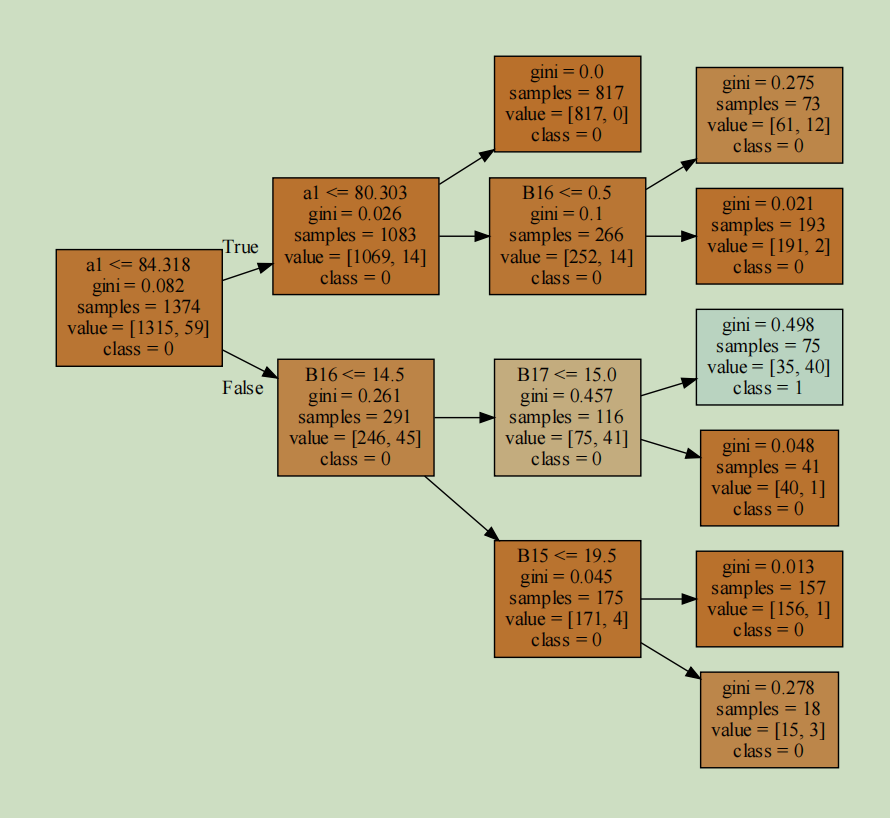
这棵CART二叉决策树预测时从根节点开始向每个非叶子字节执行一次某个特征的逻辑判断,当条件为真时走向右子树,否在走左子树;一直走到叶子结点时就可以知道被预测的标签。其中,每个结点还有三个属性,gini:该结点的信息熵值,上面的树选用的是基尼指数,也可以是熵(entropy);samples: 本子树一共包含了多少训练数据;value:本子树训练数据中各种标签类型的数据数量,例如[1315,59]说明第一类型的样本有1315条,第二类的样本有59条。
信息增益——熵,基尼指数
熵
熵,在热力学中是被用来衡量系统的不稳定的程度,而信息熵的概念是由信息论奠基人香农于1948年在论文《通信的数学原理》中提出的,它是用来量化数字信息的价值。其中信息熵的定义有以下公式
随
机
事
件
的
熵
=
H
(
P
1
,
P
2
,
.
.
.
,
P
n
)
=
−
∑
i
=
1
n
P
i
⋅
log
2
(
P
i
)
随机事件的熵=H(P_1,P_2,...,P_n)=-sum_{i=1}^nP_i cdotlog_2{(P_i)}
随机事件的熵=H(P1,P2,...,Pn)=−i=1∑nPi⋅log2(Pi)
其中
P
1
,
P
2
,
.
.
.
,
P
n
P_1,P_2,...,P_n
P1,P2,...,Pn是随机事件每种可能结果发生概率,所以必有
P
1
+
P
2
+
.
.
.
+
P
n
=
1
P_1+P_2+...+P_n=1
P1+P2+...+Pn=1,熵H()的结果是一个大于等于0的值,熵越高说明事件的不不确定性越大。而当有信息表明不确定性越大的事件结果时,说明该条信息价值越高。下面我们用一个列子来理解下这个信息熵。
有两件事情,第一件事(A)是知道下一次抛硬币的结果,另一件事(B)是知道下一次掷骰子的结果。那么事件A和B那个更有价值呢?我们用信息熵的公式计算下
事件A:
H
=
−
(
1
2
×
log
2
(
1
2
)
+
1
2
×
log
2
(
1
2
)
=
1
)
H=-(frac12timeslog_2{(frac12)}+frac12timeslog_2{(frac12)}=1)
H=−(21×log2(21)+21×log2(21)=1)
事件B:
H
=
1
6
×
log
2
(
1
6
)
+
.
.
.
.
≈
2.59
H=frac16timeslog_2{(frac16)+....}approx2.59
H=61×log2(61)+....≈2.59
显然事件B的信息价值更高。
基尼指数
基尼指数也是用来衡量信息价值的指标,既然有了完美理论依据的信息熵,为什么还会有基尼指数呢?其实是在计算机计算信息熵的计算中,
log
2
(
)
log_2()
log2()非常耗时,所有就出现了基尼指数:
随
机
事
件
的
熵
=
G
(
P
1
,
P
2
,
.
.
.
,
P
n
)
=
1
−
∑
i
=
1
n
P
i
2
随机事件的熵=G(P_1,P_2,...,P_n)=1-sum_{i=1}^nP_i^2
随机事件的熵=G(P1,P2,...,Pn)=1−i=1∑nPi2
这个公式有闭合的值域范围[0,1],数值越大表示事件越无序。虽然基尼指数衡量信息价值的能力逊于熵,但是它是由普通的乘法和加法组成,并且由封闭的取值范围,在实际开发中也经常使用。
CART 算法模型实战
CART 算法的使用场景更多,而且scikit-learn中sklean.tree包中实现了CART模型,分别用DecisionTreeClassifier和DecisionTreeRegressor实现了分类树和回归树。所有下面我们就用CART来实战,下面的数据集用的是数学建模比赛——2021年第二届“华数杯”全国大学生数学建模c题的数据,数据清洗就不展示了,有兴趣的可以去实战下数据清洗。数据下载地址,也可以在网盘下载清洗好的数据来实战
百度网盘链接:https://pan.baidu.com/s/1aj4wIElMwzLPWhuFEwZ8BQ
提取码:815c
分类树
# encoding = 'utf-8' python=3.76
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import mean_squared_error
from math import sqrt
from sklearn import tree
import graphviz
import pydotplus
import os
# 导入数据
data = pd.read_excel('C:\Users\新建文件夹\目标客户体验数据(清洗).xlsx')
test_data = pd.read_excel('C:\Users\新建文件夹\待判定的数据.xlsx')
# 清洗数据,筛选特征a1到a8和特征B13,B15,B16, B17
x_test = test_data.drop('是否会购买?', 1)
x_test1 = x_test.drop(['客户编号', '品牌编号 ', 'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B9', 'B10', 'B11', 'B12', 'B14'], 1)
x_data = data.drop('购买意愿', 1)
x_data1 = x_data.drop(['目标客户编号', '品牌类型', 'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B9', 'B10', 'B11', 'B12', 'B14'], 1)
y_data = data.loc[:, '购买意愿']
name_data = list(data.columns.values)
# 把清洗好的数据拆分成训练集和测试集
train_data, test_data, train_target, test_target = train_test_split(x_data1, y_data, test_size=0.3)
# 决策树
clf = tree.DecisionTreeClassifier(criterion="gini",
splitter="best",
max_depth=4,
min_samples_split=2,
min_samples_leaf=7,
min_weight_fraction_leaf=0.,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.,
min_impurity_split=None,
class_weight=None,
presort=False)
clf.fit(train_data, train_target.astype('int')) # 使用训练集训练模型
y_pred = clf.predict(test_data)
predict_results = clf.predict(x_test1) # 使用模型对待判定数据进行预测
scores = clf.score(test_data, test_target.astype('int'))
MSE = np.sum((y_pred-test_target)**2)/len(test_target)
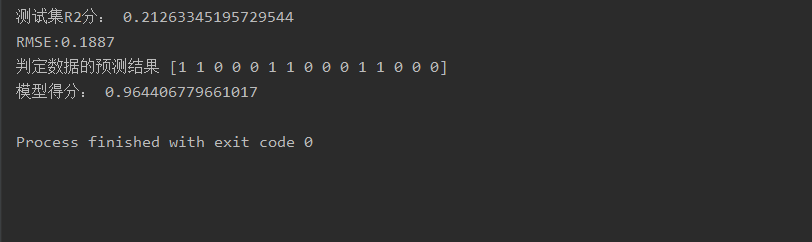
print("测试集R2分:", metrics.r2_score(test_target, y_pred.reshape(-1, 1)))
print('RMSE:{:.4f}'.format(sqrt(MSE))) # RMSE(标准误差)
print("判定数据的预测结果", predict_results)
print("模型得分:", scores)
树的可视化
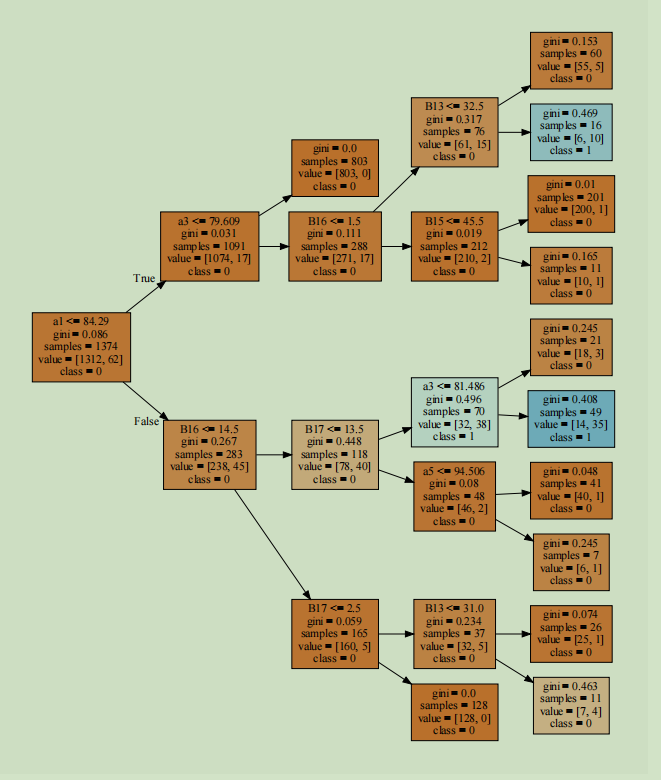
在实际应用中,选择决策树模型最主要的是模型易理解,可以快速分析各特征维度的重要程度。下面我们就把上面的树可视化下。首先,可是化树需要安装跨平台的图形库graphviz。在Windows中可以去官网下载安装程序下载地址,安装后记得要配置环境变量,控制面板——系统和安全——系统——高级系统设置——环境变量——系统变量——path。在Mac中可以直接$brew install graphviz。然后就可以直接使用export_graphviz()函数生成树的对象了
# 可视化树并保存
os.environ["PATH"] += os.pathsep + r'C:Program FilesGraphvizbin'
with open("tree.dot", 'w') as f:
f = tree.export_graphviz(clf, out_file=f)
dot_data = tree.export_graphviz(clf, out_file=None, feature_names=[u'a1', u'a2', u'a3', u'a4', u'a5', u'a6', u'a7', u'a8', u'B13', u'B15', u'B16', u'B17'],
class_names=[u'0', u'1'], filled=True, rotate=True)
graph = pydotplus.graph_from_dot_data(dot_data)
# 保存图像为pdf文件
graph.write_pdf("test1.pdf")
回归树
回归树的实战我们使用波士顿房价数据集。
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn import tree
# 导入数据集
boston = load_boston()
data = boston.data
target = boston.target
# 数据预处理
train_data, test_data, train_target, test_target = train_test_split(data, target, test_size=0.3)
Stand_X = StandardScaler() # 特征进行标准化
Stand_Y = StandardScaler() # 标签也是数值,也需要进行标准化
train_data = Stand_X.fit_transform(train_data)
test_data = Stand_X.transform(test_data)
train_target = Stand_Y.fit_transform(train_target.reshape(-1, 1)) # reshape(-1,1)指将它转化为1列,行自动确定
test_target = Stand_Y.transform(test_target.reshape(-1, 1))
# 决策树
clf = tree.DecisionTreeRegressor()
clf.fit(train_data, train_target)
y_pred = clf.predict(test_data)
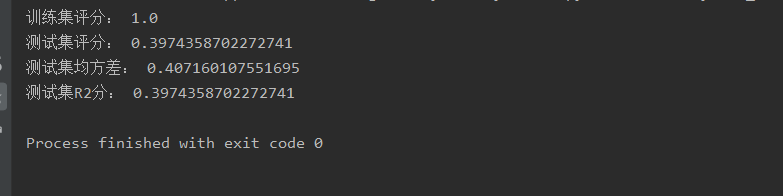
print("训练集评分:", clf.score(train_data, train_target))
print("测试集评分:", clf.score(test_data, test_target))
print("测试集均方差:", metrics.mean_squared_error(test_target, y_pred.reshape(-1, 1)))
print("测试集R2分:", metrics.r2_score(test_target, y_pred.reshape(-1, 1)))
总结
最后总结下模型的初始化参数
| 参数 | 解释 |
|---|---|
| criterion | 取值gini或者entropy,即使用基尼指数还是熵来计算信息增益 |
| splitter | 取值best或者random,作用是控制决策树中的随机选项,选择best时决策树在分枝时虽然随机,但是还是会优先选择更重要的特征进行分枝,random,决策树在分枝时会更加随机,树会因为含有更多的不必要信息而更深更大,并因这些不必要信息而降低对训练集的拟合。可以防止过拟合 |
| max_depth | 树的最大深度,限制树深度能够有效地限制过拟合 |
| min_samples_split | 继续分裂一个结点最少需要的训练样本数 |
| min_samples_leaf | 叶子结点最少含有的训练样本数 |
| max_leaf_nodes | 叶子结点的最大总数 |
| min_impurity_decrease | 用于计算叶子结点的最小纯度 |
| min_weight_fraction_leaf | 有了权重之后,这时候剪枝,就需要搭配min_ weight_fraction_leaf这个基于权重的剪枝参数来使用 |
| max_features | 分枝时考虑的特征个数 |
| random_state | 随机数种子,固定种子之后,训练的模型是一样的 |
| min_impurity_split | 不纯度必须大于这个值,不然不分裂 |
| class_weight | 标签权重,给某一类的标签更大的权重,当样本不均衡的时候,可以考虑使用 |
其中criterion,max_depth,min_samples_leaf,min_samples_split, max_leaf_nodes,min_impurity_decrease 这些参数主要围绕如何控制分裂结点特征的选取和防止过度拟合的训练后剪枝。
最后
以上就是坦率豌豆最近收集整理的关于机器学习之决策树(实战)的全部内容,更多相关机器学习之决策树(实战)内容请搜索靠谱客的其他文章。








发表评论 取消回复