决策树预剪枝：

决策树可以分成ID3、C4.5和CART。

算法目的：决策树的剪枝是为了简化决策树模型，避免过拟合。

剪枝类型：预剪枝、后剪枝

• 预剪枝：在构造决策树的同时进行剪枝。所有决策树的构建方法，都是在无法进一步降低熵的情况下才会停止创建分支的过程，为了避免过拟合，可以设定一个阈值，熵减小的数量小于这个阈值，即使还可以继续降低熵，也停止继续创建分支。但是这种方法实际中的效果并不好。
• 后剪枝是在决策树生长完成之后，对树进行剪枝，得到简化版的决策树。

  剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，熵的增加量是否小于某一阈值。如果确实小，则这一组节点可以合并一个节点，其中包含了所有可能的结果。后剪枝是目前最普遍的做法。
  后剪枝的剪枝过程是删除一些子树，然后用其叶子节点代替，这个叶子节点所标识的类别通过大多数原则(majority class criterion)确定。

预剪枝

•预剪枝就是在完全正确分类训练集之前，较早地停止树的生长。 具体在什么时候停止决策树的生长有多种不同的方法:
(1) 一种最为简单的方法就是在决策树到达一定高度的情况下就停止树的生长。
(2) 到达此结点的实例具有相同的特征向量，而不必一定属于同一类， 也可停止生长。
(3) 到达此结点的实例个数小于某一个阈值也可停止树的生长。

(4) 还有一种更为普遍的做法是计算每次扩张对系统性能的增益，如果这个增益值小于某个阈值则不进行扩展。

代码实现：

（省略基本信息熵等数学运算代码，见第一次实验）

数据集：
def createDataXG20():
    data = np.array([['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
                    , ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
                    , ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
                    , ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
                    , ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
                    , ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
                    , ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘']
                    , ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑']
                    , ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑']
                    , ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘']
                    , ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑']
                    , ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘']
                    , ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑']
                    , ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑']
                    , ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
                    , ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑']
                    , ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑']])
    label = np.array(['是', '是', '是', '是', '是', '是', '是', '是', '否', '否', '否', '否', '否', '否', '否', '否', '否'])
    name = np.array(['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'])
    return data, label, name

def splitXgData20(xgData, xgLabel):
    xgDataTrain = xgData[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16],:]
    xgDataTest = xgData[[3, 4, 7, 8, 10, 11, 12],:]
    xgLabelTrain = xgLabel[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16]]
    xgLabelTest = xgLabel[[3, 4, 7, 8, 10, 11, 12]]
    return xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest

# 创建预剪枝决策树
def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'):

    trainData = np.asarray(dataTrain)
    labelTrain = np.asarray(labelTrain)
    testData = np.asarray(dataTest)
    labelTest = np.asarray(labelTest)
    names = np.asarray(names)# 如果结果为单一结果
    if len(set(labelTrain)) == 1: 
        return labelTrain[0] # 如果没有待分类特征
    elif trainData.size == 0: 
        return voteLabel(labelTrain)# 其他情况则选取特征 
    bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method) # 取特征名称
    bestFeatName = names[bestFeat] # 从特征名称列表删除已取得特征名称
    names = np.delete(names, [bestFeat])# 根据最优特征进行分割
    dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat)# 预剪枝评估
    labelTrainLabelPre = voteLabel(labelTrain)
    labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size# 划分后的精度计算 
    if dataTest is not None: 
        dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat)# 划分前的测试标签正确比例
        labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size# 划分后 每个特征值的分类标签正确的数量
        labelTrainEqNumPost = 0
        for val in labelTrainSet.keys():
            labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0# 划分后 正确的比例
        labelTestRatioPost = labelTrainEqNumPost / labelTest.size 
# 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分
    if dataTest is None and labelTrainRatioPre == 0.5:
        decisionTree = {bestFeatName: {}}
        for featValue in dataTrainSet.keys():
            decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
                                      , None, None, names, method)
    elif dataTest is None:
        return labelTrainLabelPre 
    # 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回
    elif labelTestRatioPost < labelTestRatioPre:
        return labelTrainLabelPre
    else :
        # 根据选取的特征名称创建树节点
        decisionTree = {bestFeatName: {}}
        # 对最优特征的每个特征值所分的数据子集进行计算
        for featValue in dataTrainSet.keys():
            decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
                                      , dataTestSet.get(featValue), labelTestSet.get(featValue)
                                      , names, method)
    return decisionTree 

预剪枝测试：

# 分割为测试集和训练集
xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest = splitXgData20(xgData, xgLabel)
# 生成不剪枝的树
xgTreeTrain = createTree(xgDataTrain, xgLabelTrain, xgName, method = 'id3')
# 生成预剪枝的树
xgTreePrePruning = createTreePrePruning(xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest, xgName, method = 'id3')
# 画剪枝前的树
print("原树")
createPlot(xgTreeTrain)
# 画剪枝后的树
print("剪枝树")
createPlot(xgTreePrePruning)

输出结果对比：

   原

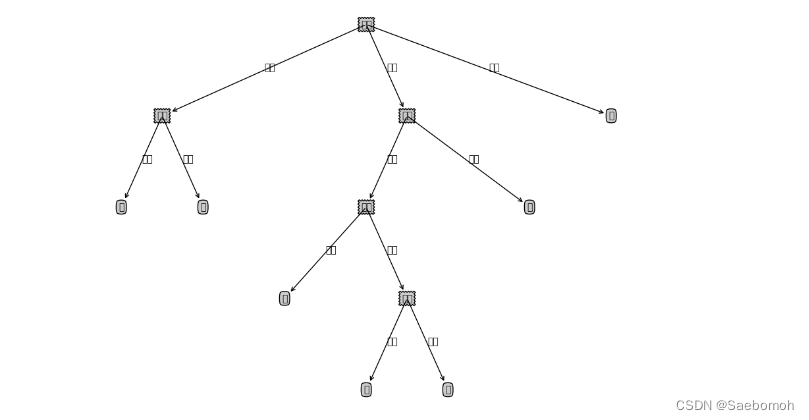
后：

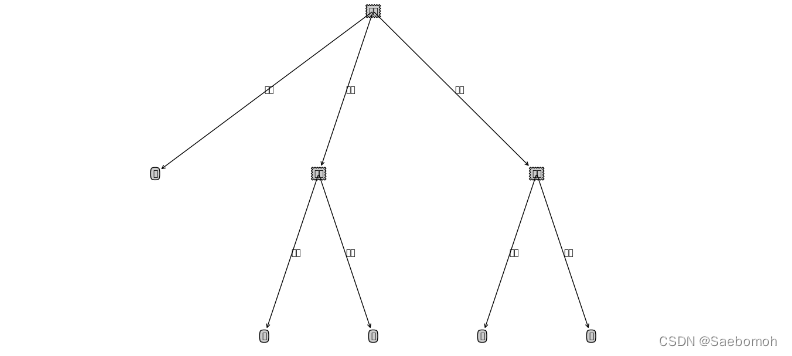
优点&缺点

•由于预剪枝不必生成整棵决策树，且算法相对简单， 效率很高， 适合解决大规模问题。但是尽管这一方法看起来很直接， 但是 怎样精确地估计何时停止树的增长是相当困难的。

•预剪枝有一个缺点， 即视野效果问题 。 也就是说在相同的标准下，也许当前的扩展会造成过度拟合训练数据，但是更进一步的扩展能够满足要求，也有可能准确地拟合训练数据。这将使得算法过早地停止决策树的构造。

如果利用可视化剪枝代码：

clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=0, min_samples_split=5)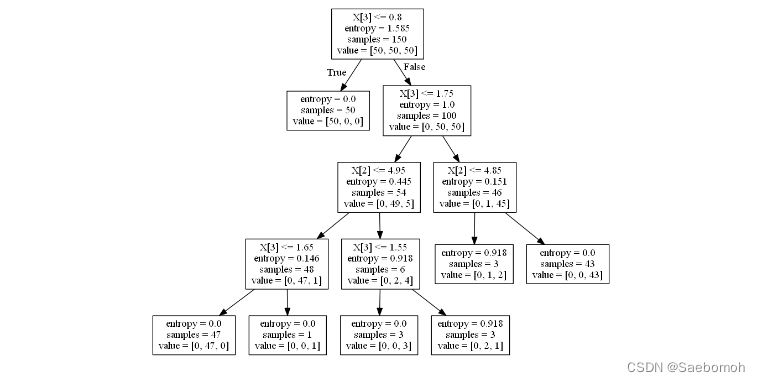

clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=0, min_samples_split=10)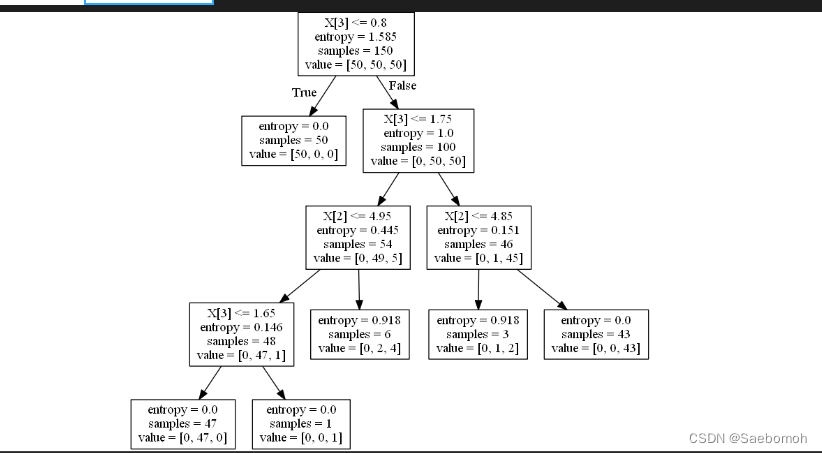

 可以知道min_samples_split的值越大，分支就越小，这就是进行了剪枝操作。

后剪枝：

后剪枝，在已生成过拟合决策树上进行剪枝，可以得到简化版的剪枝决策树

1、REP-错误率降低剪枝

2、PEP-悲观剪枝

3、CCP-代价复杂度剪枝

4、MEP-最小错误剪枝

完整代码：

import pandas as pd
import math
import treePlotter
import json
import collections
import treePlotter
from most_class_compute import most_class_computes


# 对离散变量划分数据集，取出该特征取值为value的所有样本
def splitDataSet(dataSet, axis, value):
    print"-----------------进入splitDataSet-------------------------------"
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            print"reducedFeatVec①=",json.dumps(reducedFeatVec,ensure_ascii=False)
            reducedFeatVec.extend(featVec[axis + 1:])
            print"reducedFeatVec②=",json.dumps(reducedFeatVec,ensure_ascii=False)
            retDataSet.append(reducedFeatVec)
    return retDataSet



def chooseBestFeatureToSplit(dataSet, labels):
    print"chooseBestFeatureToSplit=",json.dumps(dataSet,ensure_ascii=False)
    numFeatures = len(dataSet[0]) - 1#数据集中剩余的没有划分的特征的数量
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    bestSplitDict = {}
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        # 计算该特征下每种划分的信息熵
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = float(len(subDataSet)) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature   = i
    return bestFeature



def classify(inputTree, featLabels, testVec):
    #featLabels包含当前数据集的所有特征
    print"-------------进入classify函数-----------------"
    firstStr = list(inputTree.keys())[0]#这个是当前根节点的名称
    print"firstStr=",firstStr
    secondDict = inputTree[firstStr]#这个是当前根节点下面所有的树枝
    print"secondDict=",json.dumps(secondDict,ensure_ascii=False)
    featIndex = featLabels.index(firstStr)#
    for key in secondDict.keys():#遍历决策树模型的当前根节点下面的所有的树枝
        if testVec[featIndex] == key:#如果有一个树枝上的取值和测试向量"对应"上了,就继续递归"对应"
            if type(secondDict[key]).__name__ == 'dict':#如果当前的树枝连着一颗子树,因为如果是子树,那么字数的存储形式一定是dict类型
                classLabel = classify(secondDict[key], featLabels, testVec)#那么就进行递归判断
            else:
                classLabel = secondDict[key]#如果是叶子节点,那么测试数据的类别就是该叶子节点的内容
    print"classLabel=",classLabel
    print"type(classLabel)=",type(classLabel)
    return classLabel



def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]=0
        classCount[vote]+=1
    return max(classCount, key=classCount.get)


#这个用于预剪枝
def testing_feat(feat, train_data, test_data, labels):
    print"train_data=",json.dumps(train_data,ensure_ascii=False)
    class_list = [example[-1] for example in train_data]
    bestFeatIndex = labels.index(feat)
    train_data = [example[bestFeatIndex] for example in train_data]
    test_data = [(example[bestFeatIndex], example[-1]) for example in test_data]
    all_feat = set(train_data)
    error = 0.0
    for value in all_feat:
        class_feat = [class_list[i] for i in range(len(class_list)) if train_data[i] == value]
        major = majorityCnt(class_feat)
        for data in test_data:
            if data[0] == value and data[1] != major:
                error += 1.0
    # print 'myTree %d' % error
    return error


#这个函数用于预剪枝和后剪枝
def testingMajor(major, data_test):
    error = 0.0
    for i in range(len(data_test)):
        if major != data_test[i][-1]:
            error += 1
    # print 'major %d' % error
    return float(error) 


#这个函数专门用于"后剪枝"
def testing(myTree,data_test,labels):
    print"----------进入testing函数--------------"
    print"data_test=",json.dumps(data_test,ensure_ascii=False)

    print"labels=",json.dumps(labels,ensure_ascii=False)
    error=0.0    
    for i in range(len(data_test)):
        if classify(myTree,labels,data_test[i])!=data_test[i][-1]:#如果预测结果与验证数据的类别标签不一致
            error+=1    #那么错误数就+1
    print ('myTree %d' %error)
    return float(error)


#递归产生决策树**
def createTree(dataSet,labels,data_full,labels_full,test_data,mode):
    classList=[example[-1] for example in dataSet]
    # dataSet指的是当前的数据集,不是最初的数据集
    # classList指的是当前数据集的所有标签(不去重)

    #下面是递归截止条件
    if classList.count(classList[0])==len(classList):#这个意思是如果当前数据集中的所有数据都属于同一个类别
       return classList[0]
    if len(dataSet[0])==1:
       return majorityCnt(classList)

    #选择最佳分割特征
    #labels_copy = labels
    labels_copy = copy.deepcopy(labels)#深拷贝就是:labels_copy和lables撇清关系
    bestFeat=chooseBestFeatureToSplit(dataSet,labels)
    bestFeatLabel=labels[bestFeat]

    if mode == "unpru" or mode == "post":#因为后剪枝是"先建树-后剪枝"的思路,所以这里建了再说
        myTree = {bestFeatLabel: {}}
    elif mode == "prev":
        # 下面一句代码有2种理解方式
        #如果剪枝前的准确度大于剪枝后的准确度(第1种理解方式,与不等号左右对应)
        #如果剪枝前的错误数量小于剪枝后的错误数量(第2种理解方式,与不等号左右对应)
        #那么就保留该子树
        if testing_feat(bestFeatLabel, dataSet, test_data, labels_copy) < testingMajor(majorityCnt(classList),test_data):
            myTree = {bestFeatLabel: {}}
        else:
            return majorityCnt(classList)
            #这里的操作,相当于抹掉了前面的myTree的赋值操作,因为这里是直接返回一个叶子节点
            #也就是把根节点变成了叶子节点,实现了预剪枝操作

    featValues=[example[bestFeat] for example in dataSet]
    uniqueVals=set(featValues)
    #uniqueVals用来获得当前数据集的最佳分割属性剩余的取值有哪些

    del (labels[bestFeat])#删除根节点的已经用过的特征

    for value in uniqueVals:
    #遍历当前根节点的所有树枝,
    # 因为树枝就是当前分割节点对应的特征的取值,
    # 这些取值是剩余数据集的取值,
    # 并不是最初的所有可能的取值
    # 所以这里也会留下隐患,有些虚拟的叶子节点无法生成(虚拟叶子节点见上面的博客链接中)
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, data_full, labels_full,splitDataSet(test_data, bestFeat, value), mode=mode)

    if mode == "post":
        if testing(myTree, test_data, labels_copy)> testingMajor(majorityCnt(classList), test_data):
            return majorityCnt(classList)
            #实现后剪枝操作
            #无视当前的myThree,直接返回一个叶子节点,等效于实现了REP后剪枝

    return myTree

总结：

剪枝过程在决策树模型中占据着极其重要的地位。有很多研究表明 ，剪枝比树的生成过程更为关键。对于不同划分标准生成的过拟合决策树 ，在经过剪枝之后都能保留最重要的属性划分，因此最终的性能差距并不大 。 理解剪枝方法的理论， 在实际应用中根据不同的数据类型、规模，决定使用何种决策树以及对应的剪枝策略，灵活变通 ，找到最优选择。

参考文献：

1.王路ylu：决策树python

2.机器学习实战

3 谢小娇包教包会决策树之决策树剪枝

最后

以上就是无情山水为你收集整理的决策树第二部分预剪枝决策树预剪枝：预剪枝测试：优点&缺点后剪枝：完整代码：总结：参考文献：  的全部内容，希望文章能够帮你解决决策树第二部分预剪枝决策树预剪枝：预剪枝测试：优点&缺点后剪枝：完整代码：总结：参考文献：  所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。