LeetCode 773 LintCode 941 滑动谜题八数码问题单向bfs+双向bfs+A算法+IDA算法解法汇总一、细节说明二、具体解法

89 阅读 0 评论 59 点赞

我是靠谱客的博主害怕故事，这篇文章主要介绍LeetCode 773 LintCode 941 滑动谜题八数码问题单向bfs+双向bfs+A*算法+IDA*算法解法汇总一、细节说明二、具体解法，现在分享给大家，希望可以做个参考。

文章目录

@[toc]

一、细节说明
二、具体解法
1. bfs法
1.1 单向bfs
（1）hash法
（2）康托展开

1.2 双向bfs
（1）hash法
（2）康托展开

2. A算法
2.1 使用位置不同块数作为估计函数
（1）hash法
（2）康托展开

2.2 使用曼哈顿距离作为估计函数
（1）hash法
（2）康托展开

3. IDA算法
3.1 使用位置不同块数作为估计函数
3.2 使用曼哈顿距离作为估计函数

自己实现的LeetCode相关题解代码库：https://github.com/Yuri0314/Leetcode

自己实现的LintCode相关题解代码库：https://github.com/Yuri0314/LintCode

在这里插入图片描述

仔细看题之后发现这其实就是一道典型的八数码问题。如果把某一时刻谜板的摆放状态视为起始状态的话，那么该题即要求我们找到从该状态到最终摆放状态最短路径的步数长度，这是典型的隐式图搜索问题，可以使用多种方法求解，下面我一一进行说明。

一、细节说明

本题传入的摆放状态是二维数组的形式，因为有些解法需要对状态进行判重，所以转换为一种其他形式表示可能更为方便。

这里我们可以将其转换为一个字符串进行表示，例如：[[3,2,1],[5,0,4]]可以表示为"321504"，因此最终形式的状态表示为“123450”。在java中可以直接调用Arrays.deepToString方法将二维数组转换为字符串表示形式，但还需注意去除转换后字符串中的“[],”等符号

二、具体解法

1. bfs法

对于图搜索的问题，既可以使用bfs也可以使用dfs方法来解决，但本题要求只求最少的步数，那么使用bfs求得的解一定是步数最少的，而dfs则不一定，因此本题更宜使用bfs法

1.1 单向bfs

（1）hash法

把给定初始摆放状态作为起始点，终止状态作为目标点，每次通过将0尝试向上下左右4个方向移动来获得新的状态。此外，还需通过一个Set集合来防止走到之前已经走过的状态结点。

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        Queue<String> queue = new LinkedList<String>();
        Set<String> seen = new HashSet<String>();   // 用来判断当前摆放状态是否已经走过
        queue.add(start);
        seen.add(start);
        int steps = 0;
        while (!queue.isEmpty()) {
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                if (cur.equals("123450")) return steps;
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        if (seen.add(next)) queue.add(next);
                    }
                }
            }
            ++steps;
        }
        return -1;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        Queue<String> queue = new LinkedList<String>();
        Set<String> seen = new HashSet<String>();   // 用来判断当前摆放状态是否已经走过
        queue.add(start);
        seen.add(start);
        int steps = 0;
        while (!queue.isEmpty()) {
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                if (cur.equals("123450")) return steps;
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        if (seen.add(next)) queue.add(next);
                    }
                }
            }
            ++steps;
        }
        return -1;
    }
}

（2）康托展开

和hash法类似，此处只是将判重方式从Set集合改为一个布尔数组，使用康托展开计算每种数字排列对应的数值，然后将布尔数组中对应数值位置置为true以标识该状态结点已访问过。

康托展开是一个全排列到一个自然数的双射，常用于构建哈希表时的空间压缩。详细了解可查看说明

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        Queue<String> queue = new LinkedList<String>();
        boolean[] seen = new boolean[720];   // 用来判断当前摆放状态是否已经走过
        queue.add(start);
        seen[cantor(start)] = true;
        int steps = 0;
        while (!queue.isEmpty()) {
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                if (cur.equals("123450")) return steps;
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        int cantorNum = cantor(next);
                        if (!seen[cantorNum]) {
                            queue.add(next);
                            seen[cantorNum] = true;
                        }
                    }
                }
            }
            ++steps;
        }
        return -1;
    }

/**
     * 使用康托映射计算数字排列对应的数
     * @return
     */
    private int cantor(String s) {
        char[] chs = s.toCharArray();
        int ans = 0;
        for (int i = 0; i < 6; ++i) {
            int cnt = 0;
            for (int j = i + 1; j < 6; ++j)
                if (chs[i] > chs[j]) ++cnt;
            ans += cnt * factorial[5 - i];
        }
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        Queue<String> queue = new LinkedList<String>();
        boolean[] seen = new boolean[720];   // 用来判断当前摆放状态是否已经走过
        queue.add(start);
        seen[cantor(start)] = true;
        int steps = 0;
        while (!queue.isEmpty()) {
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                if (cur.equals("123450")) return steps;
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        int cantorNum = cantor(next);
                        if (!seen[cantorNum]) {
                            queue.add(next);
                            seen[cantorNum] = true;
                        }
                    }
                }
            }
            ++steps;
        }
        return -1;
    }

    /**
     * 使用康托映射计算数字排列对应的数
     * @return
     */
    private int cantor(String s) {
        char[] chs = s.toCharArray();
        int ans = 0;
        for (int i = 0; i < 6; ++i) {
            int cnt = 0;
            for (int j = i + 1; j < 6; ++j)
                if (chs[i] > chs[j]) ++cnt;
            ans += cnt * factorial[5 - i];
        }
        return ans;
    }
}

1.2 双向bfs

（1）hash法

除了普通的单向搜索外，bfs算法还可以转换为双向bfs来进行优化以提高算法效率。

二者最大的区别在于：单向bfs是只从起始点出发不断向四周扩展，直到找到终点为止；而双向bfs是从起始点和目标点同时出发，轮流扩展，直到二者出现交集发生相遇就停止。

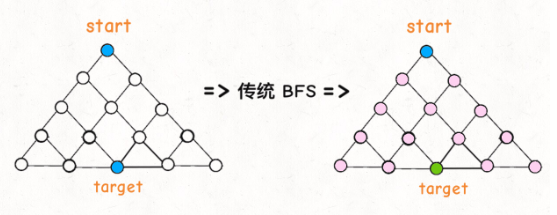
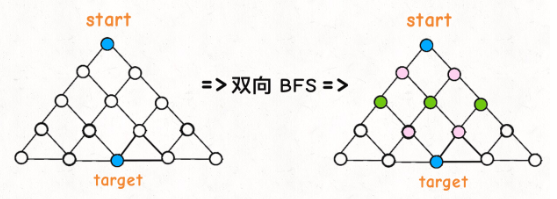
在这里插入图片描述

总体复杂度来说，与单向bfs没有区别，但是实际应用中确实能提升效率。

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        if (start.equals("123450")) return 0;
        Queue<String> queue1 = new LinkedList<String>();    // 从起点开始广搜的队列
        Queue<String> queue2 = new LinkedList<String>();    // 从终点开始广搜的队列
        Map<String, Boolean> seen = new HashMap<String, Boolean>();   // 用来判断当前摆放状态是否已经走过
        queue1.add(start); queue2.add("123450");
        seen.put(start, true); seen.put("123450", false);
        int steps = 0;
        boolean curQueue = true;
        while (!queue1.isEmpty() || !queue2.isEmpty()) {
            Queue<String> queue = curQueue ? queue1 : queue2;
            ++steps;
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        if (!seen.containsKey(next)) {
                            queue.add(next);
                            seen.put(next, curQueue);
                        }
                        else if (seen.get(cur) != seen.get(next))
                            return steps;
                    }
                }
            }
            curQueue = !curQueue;
        }
        return -1;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        if (start.equals("123450")) return 0;
        Queue<String> queue1 = new LinkedList<String>();    // 从起点开始广搜的队列
        Queue<String> queue2 = new LinkedList<String>();    // 从终点开始广搜的队列
        Map<String, Boolean> seen = new HashMap<String, Boolean>();   // 用来判断当前摆放状态是否已经走过
        queue1.add(start); queue2.add("123450");
        seen.put(start, true); seen.put("123450", false);
        int steps = 0;
        boolean curQueue = true;
        while (!queue1.isEmpty() || !queue2.isEmpty()) {
            Queue<String> queue = curQueue ? queue1 : queue2;
            ++steps;
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        if (!seen.containsKey(next)) {
                            queue.add(next);
                            seen.put(next, curQueue);
                        }
                        else if (seen.get(cur) != seen.get(next))
                            return steps;
                    }
                }
            }
            curQueue = !curQueue;
        }
        return -1;
    }
}

（2）康托展开

同单向bfs一样，同样需要判重，因此也同样可以将Set集合替换为康托展开。

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        if (start.equals("123450")) return 0;
        Queue<String> queue1 = new LinkedList<String>();    // 从起点开始广搜的队列
        Queue<String> queue2 = new LinkedList<String>();    // 从终点开始广搜的队列
        int[] seen = new int[720];   // 用来判断当前摆放状态是否已经走过
        queue1.add(start); queue2.add("123450");
        seen[cantor(start)] = 1; seen[cantor("123450")] = 2;
        int steps = 0;
        boolean curQueue = true;
        while (!queue1.isEmpty() || !queue2.isEmpty()) {
            Queue<String> queue = curQueue ? queue1 : queue2;
            ++steps;
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        int nextCantor = cantor(next);
                        if (seen[nextCantor] == 0) {
                            queue.add(next);
                            seen[nextCantor] = seen[cantor(cur)];
                        }
                        else if (seen[cantor(cur)] != seen[nextCantor])
                            return steps;
                    }
                }
            }
            curQueue = !curQueue;
        }
        return -1;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        String start = Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""); // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        if (start.equals("123450")) return 0;
        Queue<String> queue1 = new LinkedList<String>();    // 从起点开始广搜的队列
        Queue<String> queue2 = new LinkedList<String>();    // 从终点开始广搜的队列
        int[] seen = new int[720];   // 用来判断当前摆放状态是否已经走过
        queue1.add(start); queue2.add("123450");
        seen[cantor(start)] = 1; seen[cantor("123450")] = 2;
        int steps = 0;
        boolean curQueue = true;
        while (!queue1.isEmpty() || !queue2.isEmpty()) {
            Queue<String> queue = curQueue ? queue1 : queue2;
            ++steps;
            for (int sz = queue.size(); sz > 0; --sz) {
                String cur = queue.remove();
                int pos = cur.indexOf("0");
                int x = pos / colNum, y = pos % colNum;
                for (int[] move: moves) {
                    int newX = x + move[0], newY = y + move[1];
                    if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                        char[] chs = cur.toCharArray();
                        int newPos = newX * colNum + newY;
                        chs[pos] = chs[newPos];
                        chs[newPos] = '0';
                        String next = String.valueOf(chs);
                        int nextCantor = cantor(next);
                        if (seen[nextCantor] == 0) {
                            queue.add(next);
                            seen[nextCantor] = seen[cantor(cur)];
                        }
                        else if (seen[cantor(cur)] != seen[nextCantor])
                            return steps;
                    }
                }
            }
            curQueue = !curQueue;
        }
        return -1;
    }

    /**
     * 使用康托映射计算数字排列对应的数
     * @return
     */
    private int cantor(String s) {
        char[] chs = s.toCharArray();
        int ans = 0;
        for (int i = 0; i < 6; ++i) {
            int cnt = 0;
            for (int j = i + 1; j < 6; ++j)
                if (chs[i] > chs[j]) ++cnt;
            ans += cnt * factorial[5 - i];
        }
        return ans;
    }
}

2. A*算法

在一般的图搜索问题中，普通的bfs算法一般效率并不高，并且随着问题规模的不断变大，其难以搜到结果。究其原因，主要是因为bfs在搜索方向上是盲目的，随着BFS搜寻的深度加大，需要遍历的结点数量也会越来越多，而其中很多结点因为偏离了正确的方向其实是没必要访问的，它们无法导向最短的正确路径。

考虑到上述bfs方法存在的不足，A*算法对bfs方法进行了改进，使得搜索具有一定目标性，从而免去了对一些不必要的路径搜索。其想法也很简单，在BFS中当前结点 n 相对于起点的走过距离 g(n) 是已知的，但当前结点相对于目标结点需要的实际距离 *h(n) 是未知的，那么我们可以以某种方式对其进行估算得到 h(n)，然后总是选择估算总距离 f(n)=g(n)+h(n) 最小的路径，以缩小候选路径范围，从而快速找到最短路径。

A*算法的关键就在于这个h(n)函数的选择上，该函数也被称为启发式函数，根据它与离目标的实际 *h(n) 大小关系的不同，实现的A*算法也会演化成不同效率的算法。关于A*算法的更详细说明，可以参考说明。

在实现上，对bfs方法最大的修改在于将普通队列改为优先级队列，然后每次取出元素根据其估算距离f(n)进行选择弹出。此外，在判重上也需要进行修改，每次在对一个状态结点进行扩展时不仅需要判断扩展的状态是否已访问过，还需要判断其之前是被从哪个方向出发搜索的顺序访问过。

2.1 使用位置不同块数作为估计函数

（1）hash法

使用最简单的估计函数来估计当前状态与最终状态之间的距离。例如：[[3,2,1],[5,0,4]]除了2在其最终状态对应的位置上外，其余都不在（不考虑0），因此其估计距离为4。

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final String target = "123450";
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        Set<String> seen = new HashSet<String>();   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            if (cur.boardStr.equals(target)) return cur.steps;
            if (seen.contains(cur.boardStr)) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen.contains(nextStr)) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen.add(cur.boardStr);
        }
        return -1;
    }

private class State {
        String boardStr;
        int steps;
        int heuristic;
        /**
         * 使用当前状态与目标状态的对应位置不同块数计算
         * @param board
         * @param steps
         */
        State(String boardStr, int steps) {
            this.boardStr = boardStr;
            this.steps = steps;
            heuristic = 0;
            char[] boardChars = boardStr.toCharArray();
            char[] targetChars = target.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                if (boardChars[i] != targetChars[i]) ++heuristic;
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final String target = "123450";
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        Set<String> seen = new HashSet<String>();   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            if (cur.boardStr.equals(target)) return cur.steps;
            if (seen.contains(cur.boardStr)) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen.contains(nextStr)) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen.add(cur.boardStr);
        }
        return -1;
    }

    private class State {
        String boardStr;
        int steps;
        int heuristic;
        /**
         * 使用当前状态与目标状态的对应位置不同块数计算
         * @param board
         * @param steps
         */
        State(String boardStr, int steps) {
            this.boardStr = boardStr;
            this.steps = steps;
            heuristic = 0;
            char[] boardChars = boardStr.toCharArray();
            char[] targetChars = target.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                if (boardChars[i] != targetChars[i]) ++heuristic;
            }
        }
    }
}

（2）康托展开

类似，将判重集合用数组表示，用康托展开找到状态序列对应索引。

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    private final String target = "123450";
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        boolean[] seen = new boolean[720];   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            int cantorNum = cantor(cur.boardStr);
            if (cur.boardStr.equals(target)) return cur.steps;
            if (seen[cantorNum]) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen[cantor(nextStr)]) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen[cantorNum] = true;
        }
        return -1;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    private final String target = "123450";
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        boolean[] seen = new boolean[720];   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            int cantorNum = cantor(cur.boardStr);
            if (cur.boardStr.equals(target)) return cur.steps;
            if (seen[cantorNum]) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen[cantor(nextStr)]) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen[cantorNum] = true;
        }
        return -1;
    }

    /**
     * 使用康托映射计算数字排列对应的数
     * @return
     */
    private int cantor(String s) {
        char[] chs = s.toCharArray();
        int ans = 0;
        for (int i = 0; i < 6; ++i) {
            int cnt = 0;
            for (int j = i + 1; j < 6; ++j)
                if (chs[i] > chs[j]) ++cnt;
            ans += cnt * factorial[5 - i];
        }
        return ans;
    }

    private class State {
        String boardStr;
        int steps;
        int heuristic;
        /**
         * 使用当前状态与目标状态的对应位置不同块数计算
         * @param board
         * @param steps
         */
        State(String boardStr, int steps) {
            this.boardStr = boardStr;
            this.steps = steps;
            heuristic = 0;
            char[] boardChars = boardStr.toCharArray();
            char[] targetChars = target.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                if (boardChars[i] != targetChars[i]) ++heuristic;
            }
        }
    }
}

2.2 使用曼哈顿距离作为估计函数

（1）hash法

曼哈顿距离公式：

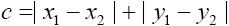
同样以[[3,2,1],[5,0,4]]举例，数字3应该在(0,2)的位置上，而其现在在(0,0)位置上，因此它的曼哈顿距离为2，同理可得最终的估计结果为：2+2+1+2=7

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[][] sheet={
        {0,0},{0,1},{0,2},
        {1,0},{1,1},{1,2}
    };
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        Set<String> seen = new HashSet<String>();   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            if (cur.boardStr.equals("123450")) return cur.steps;
            if (seen.contains(cur.boardStr)) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen.contains(nextStr)) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen.add(cur.boardStr);
        }
        return -1;
    }

private class State {
        String boardStr;
        int steps;
        int heuristic;
        /**
         * 使用曼哈顿距离计算
         * @param board
         * @param steps
         */
        State(String boardStr, int steps) {
            this.boardStr = boardStr;
            this.steps = steps;
            heuristic = 0;
            char[] boardChars = boardStr.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                int val = boardChars[i] - '0' - 1;
                heuristic += Math.abs(sheet[i][0] - sheet[val][0]) + Math.abs(sheet[i][1] - sheet[val][1]);
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[][] sheet={
        {0,0},{0,1},{0,2},
        {1,0},{1,1},{1,2}
    };
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        Set<String> seen = new HashSet<String>();   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            if (cur.boardStr.equals("123450")) return cur.steps;
            if (seen.contains(cur.boardStr)) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen.contains(nextStr)) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen.add(cur.boardStr);
        }
        return -1;
    }

    private class State {
        String boardStr;
        int steps;
        int heuristic;
        /**
         * 使用曼哈顿距离计算
         * @param board
         * @param steps
         */
        State(String boardStr, int steps) {
            this.boardStr = boardStr;
            this.steps = steps;
            heuristic = 0;
            char[] boardChars = boardStr.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                int val = boardChars[i] - '0' - 1;
                heuristic += Math.abs(sheet[i][0] - sheet[val][0]) + Math.abs(sheet[i][1] - sheet[val][1]);
            }
        }
    }
}

（2）康托展开

复制代码

class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    private final int[][] sheet={
        {0,0},{0,1},{0,2},
        {1,0},{1,1},{1,2}
    };
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        boolean[] seen = new boolean[720];   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            int cantorNum = cantor(cur.boardStr);
            if (cur.boardStr.equals("123450")) return cur.steps;
            if (seen[cantorNum]) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen[cantor(nextStr)]) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen[cantorNum] = true;
        }
        return -1;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class Solution {
    private final int[][] moves = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    private final int[] factorial = {1, 1, 2, 6, 24, 120};
    private final int[][] sheet={
        {0,0},{0,1},{0,2},
        {1,0},{1,1},{1,2}
    };
    public int slidingPuzzle(int[][] board) {
        int rowNum = board.length, colNum = board[0].length;
        Queue<State> heap = new PriorityQueue<State>((a, b) -> (a.steps + a.heuristic) - (b.steps + b.heuristic));
        boolean[] seen = new boolean[720];   // 用来判断当前摆放状态是否已经走过
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""), 0);    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        heap.add(start);
        while (!heap.isEmpty()) {
            State cur = heap.remove();
            int cantorNum = cantor(cur.boardStr);
            if (cur.boardStr.equals("123450")) return cur.steps;
            if (seen[cantorNum]) continue;
            int pos = cur.boardStr.indexOf("0");
            int x = pos / colNum, y = pos % colNum;
            for (int[] move: moves) {
                int newX = x + move[0], newY = y + move[1];
                if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                    char[] chs = cur.boardStr.toCharArray();
                    int newPos = newX * colNum + newY;
                    chs[pos] = chs[newPos];
                    chs[newPos] = '0';
                    String nextStr = String.valueOf(chs);
                    if (!seen[cantor(nextStr)]) {
                        State next = new State(nextStr, cur.steps + 1);
                        heap.add(next);
                    }
                }
            }
            seen[cantorNum] = true;
        }
        return -1;
    }

    /**
     * 使用康托映射计算数字排列对应的数
     * @return
     */
    private int cantor(String s) {
        char[] chs = s.toCharArray();
        int ans = 0;
        for (int i = 0; i < 6; ++i) {
            int cnt = 0;
            for (int j = i + 1; j < 6; ++j)
                if (chs[i] > chs[j]) ++cnt;
            ans += cnt * factorial[5 - i];
        }
        return ans;
    }

    private class State {
        String boardStr;
        int steps;
        int heuristic;
        /**
         * 使用曼哈顿距离计算
         * @param board
         * @param steps
         */
        State(String boardStr, int steps) {
            this.boardStr = boardStr;
            this.steps = steps;
            heuristic = 0;
            char[] boardChars = boardStr.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                int val = boardChars[i] - '0' - 1;
                heuristic += Math.abs(sheet[i][0] - sheet[val][0]) + Math.abs(sheet[i][1] - sheet[val][1]);
            }
        }
    }
}

3. IDA*算法

IDA*算法是A*算法和迭代加深算法的结合。

迭代加深算法是在dfs搜索算法的基础上逐步加深搜索的深度，它避免了广度优先搜索占用搜索空间太大的缺点，也减少了深度优先搜索的盲目性。它主要是在递归搜索函数的开头判断当前搜索的深度是否大于预定义的最大搜索深度，如果大于，就退出这一层的搜索，如果不大于，就继续进行搜索。这样最终获得的解必然是最优解。

而在A*算法中，我们通过使用合理的估价函数，然后在获得的子节点中选择fCost最小的节点进行扩展，以此完成搜索最优解的目的。但是A*算法中，需要维护open列表和close列表，需要对扩展出来的节点进行检测，忽略已经进入到close列表中的节点（也就是所谓的“已经检测过的节点”），另外也要检测是否与待扩展的节点重复，如果重复进行相应的更新操作。所以A*算法主要的代价花在了状态检测和选择代价最小节点的排序上，这个过程中占用的内存是比较大的，一般为了提高效率都是使用hash进行重复状态检测。

IDA*的基本思路是：首先将初始状态结点的H值设为阈值maxH，然后进行深度优先搜索，搜索过程中忽略所有H值大于maxH的结点（即剪枝）；如果没有找到解，则加大阈值maxH，再重复上述搜索，直到找到一个解。在保证H值的计算满足A*算法的要求下，可以证明找到的这个解一定是最优解。在程序实现上，IDA* 要比 A* 方便，因为不需要保存结点，不需要判重复，也不需要根据 H值对结点排序，占用空间小。而这里在IDA*算法中也使用合适的估价函数，来评估与目标状态的距离。

在一般的问题中是这样使用IDA*算法的，当前局面的估价函数值+当前的搜索深度 > 预定义的最大搜索深度时，就进行剪枝。

因为同样需要使用估计函数，我同样用了A*中的两种估计函数分别实现（设定的最大搜索深度为20，该值可以根据问题不同和需求不同进行修改，但如果设定太小小于了实际需要的最小步数，则无法找到最终解）。

3.1 使用位置不同块数作为估计函数

复制代码

class Solution {
    private int rowNum;
    private int colNum;
    private int bound;
    private int steps;
    private final int[][] moves = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
    private final String target = "123450";
    
    public int slidingPuzzle(int[][] board) {
        rowNum = board.length; colNum = board[0].length;
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""));    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        bound = start.cost; // 用当前状态的代价估计值来初始化最大界限深度
        steps = 0;
        while (!dfs(start, 0, 4) && bound < 20) ++bound;    // 限定最大搜索深度为20
        return bound < 20 ? steps : -1;
    }

private boolean dfs(State cur, int steps, int lastDir) {
        if (cur.cost + steps > bound) return false;
        if (cur.boardStr.equals(target)) {
            this.steps = steps;
            return true;
        } 
        int pos = cur.boardStr.indexOf("0");
        int x = pos / colNum, y = pos % colNum;
        for (int i = 0; i < 4; ++i) {
            if (i + lastDir == 3) continue; // 防止走回头路
            int newX = x + moves[i][0], newY = y + moves[i][1];
            if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                char[] chs = cur.boardStr.toCharArray();
                int newPos = newX * colNum + newY;
                chs[pos] = chs[newPos];
                chs[newPos] = '0';
                State next = new State(String.valueOf(chs));
                if (dfs(next, steps + 1, i)) return true;
            }
        }
        return false;
    }

private class State {
        String boardStr;
        int cost;
        /**
         * 使用当前状态与目标状态的对应位置不同块数计算
         * @param board
         * @param steps
         */
        State(String boardStr) {
            this.boardStr = boardStr;
            cost = 0;
            char[] boardChars = boardStr.toCharArray();
            char[] targetChars = target.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                if (boardChars[i] != targetChars[i]) ++cost;
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    private int rowNum;
    private int colNum;
    private int bound;
    private int steps;
    private final int[][] moves = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
    private final String target = "123450";
    
    public int slidingPuzzle(int[][] board) {
        rowNum = board.length; colNum = board[0].length;
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""));    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        bound = start.cost; // 用当前状态的代价估计值来初始化最大界限深度
        steps = 0;
        while (!dfs(start, 0, 4) && bound < 20) ++bound;    // 限定最大搜索深度为20
        return bound < 20 ? steps : -1;
    }

    private boolean dfs(State cur, int steps, int lastDir) {
        if (cur.cost + steps > bound) return false;
        if (cur.boardStr.equals(target)) {
            this.steps = steps;
            return true;
        } 
        int pos = cur.boardStr.indexOf("0");
        int x = pos / colNum, y = pos % colNum;
        for (int i = 0; i < 4; ++i) {
            if (i + lastDir == 3) continue; // 防止走回头路
            int newX = x + moves[i][0], newY = y + moves[i][1];
            if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                char[] chs = cur.boardStr.toCharArray();
                int newPos = newX * colNum + newY;
                chs[pos] = chs[newPos];
                chs[newPos] = '0';
                State next = new State(String.valueOf(chs));
                if (dfs(next, steps + 1, i)) return true;
            }
        }
        return false;
    } 

    private class State {
        String boardStr;
        int cost;
        /**
         * 使用当前状态与目标状态的对应位置不同块数计算
         * @param board
         * @param steps
         */
        State(String boardStr) {
            this.boardStr = boardStr;
            cost = 0;
            char[] boardChars = boardStr.toCharArray();
            char[] targetChars = target.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                if (boardChars[i] != targetChars[i]) ++cost;
            }
        }
    }
}

3.2 使用曼哈顿距离作为估计函数

复制代码

class Solution {
    private int rowNum;
    private int colNum;
    private int bound;
    private int steps;
    private final int[][] moves = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
    private final int[][] sheet={
        {0,0},{0,1},{0,2},
        {1,0},{1,1},{1,2}
    };
    
    public int slidingPuzzle(int[][] board) {
        rowNum = board.length; colNum = board[0].length;
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""));    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        bound = start.cost; // 用当前状态的代价估计值来初始化最大界限深度
        steps = 0;
        while (!dfs(start, 0, 4) && bound < 20) ++bound;    // 限定最大搜索深度为20，可更改
        return bound < 20 ? steps : -1;
    }

private boolean dfs(State cur, int steps, int lastDir) {
        if (cur.cost + steps > bound) return false;
        if (cur.boardStr.equals("123450")) {
            this.steps = steps;
            return true;
        } 
        int pos = cur.boardStr.indexOf("0");
        int x = pos / colNum, y = pos % colNum;
        for (int i = 0; i < 4; ++i) {
            if (i + lastDir == 3) continue; // 防止走回头路
            int newX = x + moves[i][0], newY = y + moves[i][1];
            if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                char[] chs = cur.boardStr.toCharArray();
                int newPos = newX * colNum + newY;
                chs[pos] = chs[newPos];
                chs[newPos] = '0';
                State next = new State(String.valueOf(chs));
                if (dfs(next, steps + 1, i)) return true;
            }
        }
        return false;
    }

private class State {
        String boardStr;
        int cost;
        /**
         * 使用曼哈顿距离计算
         * @param board
         * @param steps
         */
        State(String boardStr) {
            this.boardStr = boardStr;
            cost = 0;
            char[] boardChars = boardStr.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                int val = boardChars[i] - '0' - 1;
                cost += Math.abs(sheet[i][0] - sheet[val][0]) + Math.abs(sheet[i][1] - sheet[val][1]);
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
    private int rowNum;
    private int colNum;
    private int bound;
    private int steps;
    private final int[][] moves = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
    private final int[][] sheet={
        {0,0},{0,1},{0,2},
        {1,0},{1,1},{1,2}
    };
    
    public int slidingPuzzle(int[][] board) {
        rowNum = board.length; colNum = board[0].length;
        State start = new State(Arrays.deepToString(board).replaceAll("[\[\]\,\s]", ""));    // 将整个棋盘的当前摆放状态转换为一个字符串来存储表示
        bound = start.cost; // 用当前状态的代价估计值来初始化最大界限深度
        steps = 0;
        while (!dfs(start, 0, 4) && bound < 20) ++bound;    // 限定最大搜索深度为20，可更改
        return bound < 20 ? steps : -1;
    }

    private boolean dfs(State cur, int steps, int lastDir) {
        if (cur.cost + steps > bound) return false;
        if (cur.boardStr.equals("123450")) {
            this.steps = steps;
            return true;
        } 
        int pos = cur.boardStr.indexOf("0");
        int x = pos / colNum, y = pos % colNum;
        for (int i = 0; i < 4; ++i) {
            if (i + lastDir == 3) continue; // 防止走回头路
            int newX = x + moves[i][0], newY = y + moves[i][1];
            if (newX >= 0 && newX < rowNum && newY >= 0 && newY < colNum) {
                char[] chs = cur.boardStr.toCharArray();
                int newPos = newX * colNum + newY;
                chs[pos] = chs[newPos];
                chs[newPos] = '0';
                State next = new State(String.valueOf(chs));
                if (dfs(next, steps + 1, i)) return true;
            }
        }
        return false;
    } 

    private class State {
        String boardStr;
        int cost;
        /**
         * 使用曼哈顿距离计算
         * @param board
         * @param steps
         */
        State(String boardStr) {
            this.boardStr = boardStr;
            cost = 0;
            char[] boardChars = boardStr.toCharArray();
            for (int i = 0; i < 6; ++i) {
                if (boardChars[i] == '0') continue;
                int val = boardChars[i] - '0' - 1;
                cost += Math.abs(sheet[i][0] - sheet[val][0]) + Math.abs(sheet[i][1] - sheet[val][1]);
            }
        }
    }
}

最后

以上就是害怕故事最近收集整理的关于LeetCode 773 LintCode 941 滑动谜题八数码问题单向bfs+双向bfs+A*算法+IDA*算法解法汇总一、细节说明二、具体解法的全部内容，更多相关LeetCode内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：算法
浏览次数：89 次浏览
发布日期：2023-05-30 22:38:01
本文链接：https://www.kaopuke.com/article/k-p-k_14_ujogfz_13__23__22_5.html

LeetCode 773 LintCode 941 滑动谜题八数码问题单向bfs+双向bfs+A算法+IDA算法解法汇总一、细节说明二、具体解法

文章目录

一、细节说明

二、具体解法

1. bfs法

1.1 单向bfs

（1）hash法

（2）康托展开

1.2 双向bfs

（1）hash法

（2）康托展开

2. A*算法

2.1 使用位置不同块数作为估计函数

（1）hash法

（2）康托展开

2.2 使用曼哈顿距离作为估计函数

（1）hash法

（2）康托展开

3. IDA*算法

3.1 使用位置不同块数作为估计函数

3.2 使用曼哈顿距离作为估计函数

最后

评论列表共有 0 条评论

发表评论取消回复

LeetCode 773 LintCode 941 滑动谜题 八数码问题 单向bfs+双向bfs+A*算法+IDA*算法解法汇总一、 细节说明二、 具体解法

文章目录

一、 细节说明

二、 具体解法

1. bfs法

1.1 单向bfs

（1）hash法

（2）康托展开

1.2 双向bfs

（1）hash法

（2）康托展开

2. A*算法

2.1 使用位置不同块数作为估计函数

（1）hash法

（2）康托展开

2.2 使用曼哈顿距离作为估计函数

（1）hash法

（2）康托展开

3. IDA*算法

3.1 使用位置不同块数作为估计函数

3.2 使用曼哈顿距离作为估计函数

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

微信扫一扫：分享

LeetCode 773 LintCode 941 滑动谜题八数码问题单向bfs+双向bfs+A算法+IDA算法解法汇总一、细节说明二、具体解法

一、细节说明

二、具体解法

发表评论取消回复