1. 首页
  2. 文章中心
  3. 人工智能

混沌分形之迭代函数系统（IFS）

68 阅读 0 评论
我是靠谱客的博主 自然大碗，最近开发中收集的这篇文章主要介绍混沌分形之迭代函数系统（IFS），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

      IFS是分形的重要分支。它是分形图像处理中最富生命力而且最具有广阔应用前景的领域之一。这一工作最早可以追溯到Hutchinson于1981年对自相似集的研究。美国科学家M.F.Barnsley于1985年发展了这一分形构型系统，并命名为迭代函数系统（Iterated Function System，IFS），后来又由Stephen Demko等人将其公式化，并引入到图像合成领域中。IFS将待生成的图像看做是由许多与整体相似的（自相似）或经过一定变换与整体相似的（自仿射）小块拼贴而成。
算法：
1.设定一个起始点（x0，y0）及总的迭代步数。
2.以概率P选取仿射变换W，形式为
     X1=a*x0 + b*y0 + e
     Y1=c*x0 + d*y0 + f
或
     X1=(a * x0*cosf(c/180)) - (b * y0*sinf(d/180)) + e
     Y1=(a * x0*sinf(c/180)) + (b * y0*cosf(d/180)) + f
3.以W作用点（x0，y0），得到新坐标（x1，y1）。
4.令x0=x1，y0=y1。
5.在屏幕上打出（x0，y0）。
6.重返第2步，进行下一次迭代，直到迭代次数大于总步数为止。

（1）三角形

class IFSTriangle : public FractalEquation
{
public:
    IFSTriangle()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = 0.0f;
        m_ParamB = 0.5f;

        //'IFS码赋值
        m[0][0] = 0.5f; m[0][1] = 0; m[0][2] = 0;  m[0][3] = 0.5f;  m[0][4] = 0;     m[0][5] = 0;    m[0][6] = 0.333f;
        m[1][0] = 0.5f; m[1][1] = 0; m[1][2] = 0;  m[1][3] = 0.5f;  m[1][4] = 0.5f;  m[1][5] = 0;    m[1][6] = 0.333f;
        m[2][0] = 0.5f; m[2][1] = 0; m[2][2] = 0;  m[2][3] = 0.5f;  m[2][4] = 0.25f; m[2][5] = 0.5f; m[2][6] = 0.334f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float a, b, c, d, e, f;    //'仿射变幻中的系数

        float R = (float)rand()/RAND_MAX;

        if (R <= m[0][6]) 
        {
            a = m[0][0]; b = m[0][1]; c = m[0][2]; d = m[0][3]; e = m[0][4]; f = m[0][5];
        } 
        else if (R <= m[0][6] + m[1][6]) 
        {
            a = m[1][0]; b = m[1][1]; c = m[1][2]; d = m[1][3]; e = m[1][4]; f = m[1][5];
        } 
        else
        {
            a = m[2][0]; b = m[2][1]; c = m[2][2]; d = m[2][3]; e = m[2][4]; f = m[2][5];
        } 

        outX = (a * x) + (b * y) + e*FRACTAL_RADIUS;
        outY = (c * x) + (d * y) + f*FRACTAL_RADIUS;
        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}

    void SetParamA(float v)
    {
        m_ParamA = v;
        m[2][1] = v; 
    }

    void SetParamB(float v)
    {
        m_ParamB = v;
        m[2][0] = v; 
        m[0][3] = v; 
    }

private:
    float m[3][7];      // '存放IFS码
};

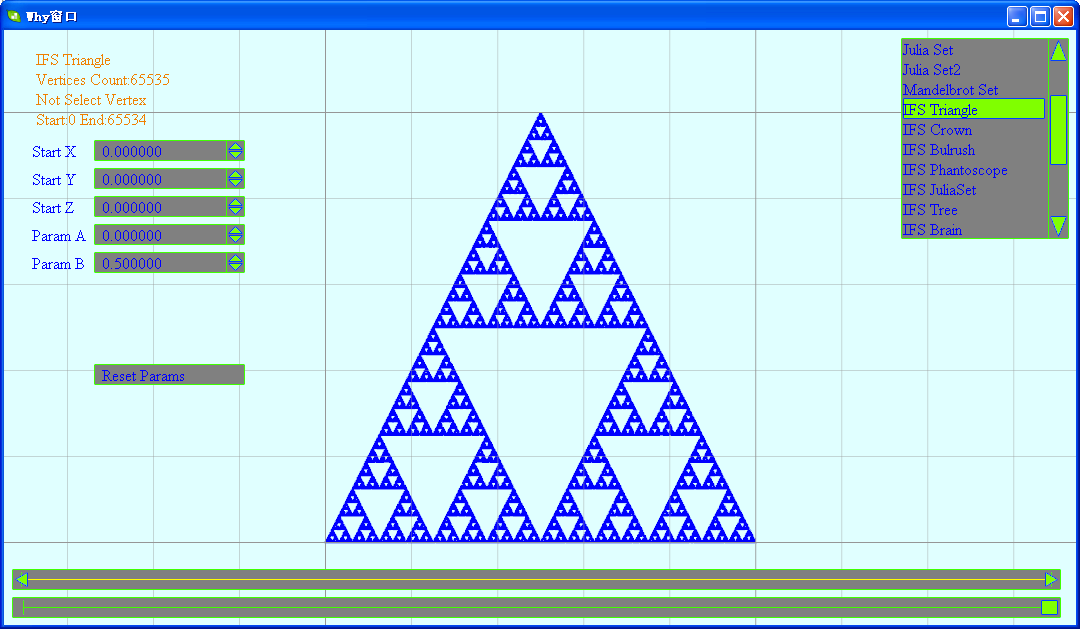
这里生成的是谢尔宾斯基三角形，但可以通过参数设置对其变形

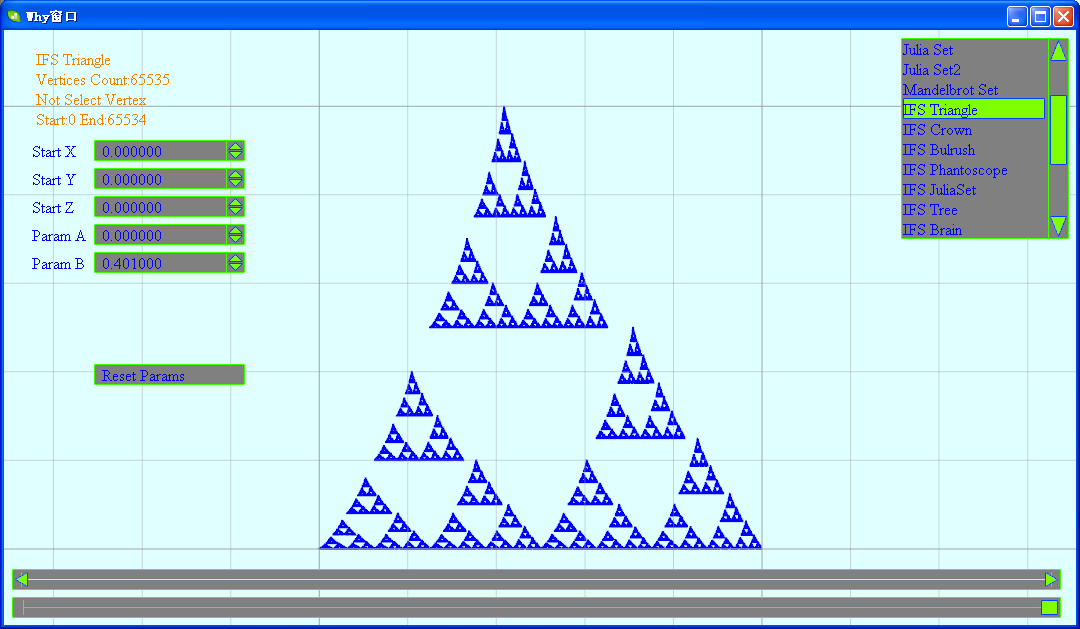
（2）皇冠

class IFSCrown : public FractalEquation
{
public:
    IFSCrown()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = 2.0f;

        //'IFS码赋值
        m[0][0] = 0.5f;   m[0][1] = 0.5f;   m[0][2] = 0;  m[0][3] = 0;  m[0][4] = 0;    m[0][5] = 0;   m[0][6] = 0.2f;
        m[1][0] = 0.5f;   m[1][1] = 0.5f;   m[1][2] = 0;  m[1][3] = 0;  m[1][4] = 0.5f; m[1][5] = 0;   m[1][6] = 0.2f;
        m[2][0] = 0.25f;  m[2][1] = 0.25f;  m[2][2] = 0;  m[2][3] = 0;  m[2][4] = 2.0f; m[2][5] = 2.0f;m[2][6] = 0.3f;
        m[3][0] = 0.25f;  m[3][1] = 0.25f;  m[3][2] = 0;  m[3][3] = 0;  m[3][4] = -1.0f;m[3][5] = 2.0f;m[3][6] = 0.3f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float a, b, c, d, e, f;    //'仿射变幻中的系数

        float R = (float)rand()/RAND_MAX;

        if (R <= m[0][6]) 
        {
            a = m[0][0]; b = m[0][1]; c = m[0][2]; d = m[0][3]; e = m[0][4]; f = m[0][5];
        } 
        else if (R <= m[0][6] + m[1][6]) 
        {
            a = m[1][0]; b = m[1][1]; c = m[1][2]; d = m[1][3]; e = m[1][4]; f = m[1][5];
        } 
        else if (R <= m[0][6] + m[1][6] + m[2][6]) 
        {
            a = m[2][0]; b = m[2][1]; c = m[2][2]; d = m[2][3]; e = m[2][4]; f = m[2][5];
        } 
        else 
        {
            a = m[3][0]; b = m[3][1]; c = m[3][2]; d = m[3][3]; e = m[3][4]; f = m[3][5];
        }

        outX = (a * x*cosf(c/180)) - (b * y*sinf(d/180)) + e*FRACTAL_RADIUS;
        outY = (a * x*sinf(c/180)) + (b * y*cosf(d/180)) + f*FRACTAL_RADIUS;
        outZ = z;
    }

    bool IsValidParamA() const {return true;}

    void SetParamA(float v)
    {
        m_ParamA = v;
        m[2][4] = v; 
        m[2][5] = v;
        m[3][4] = 1 - v;
        m[3][5] = v;
    }

private:
    float m[4][7];      // '存放IFS码
};

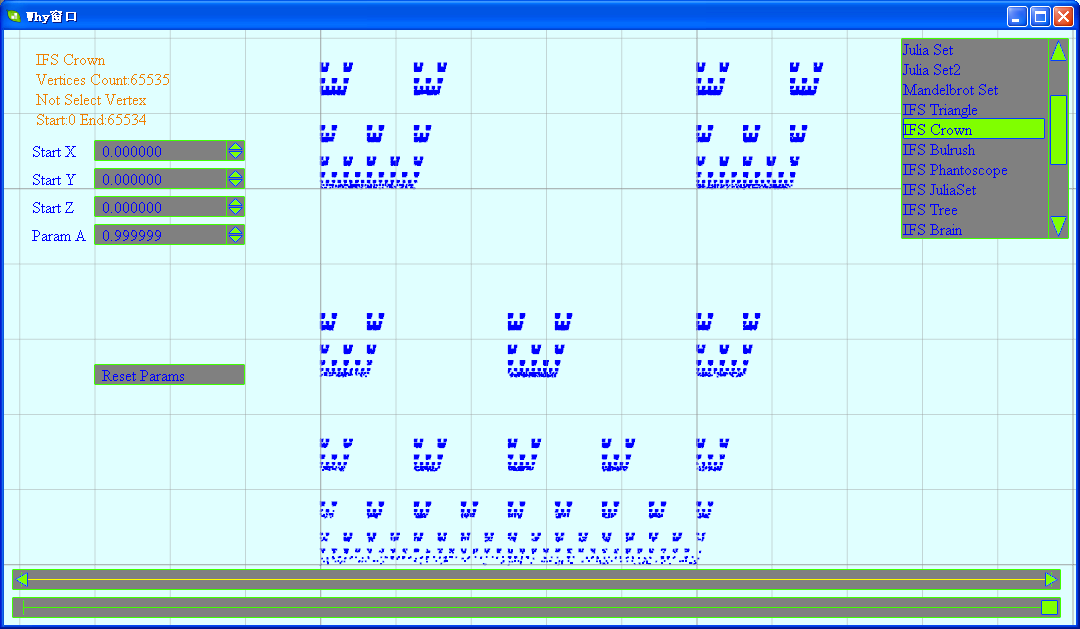
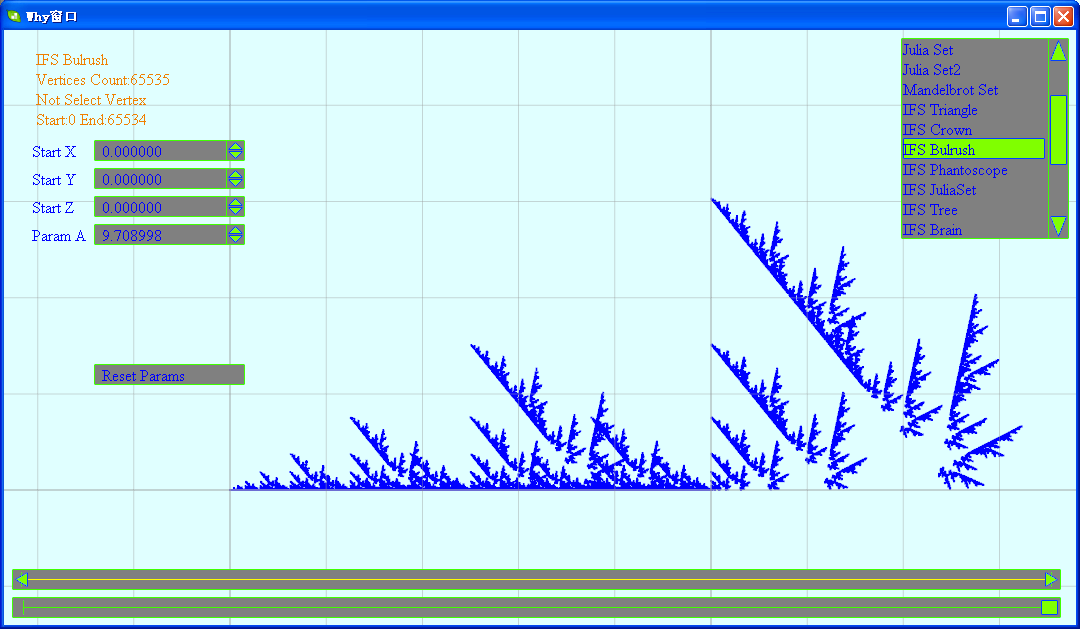
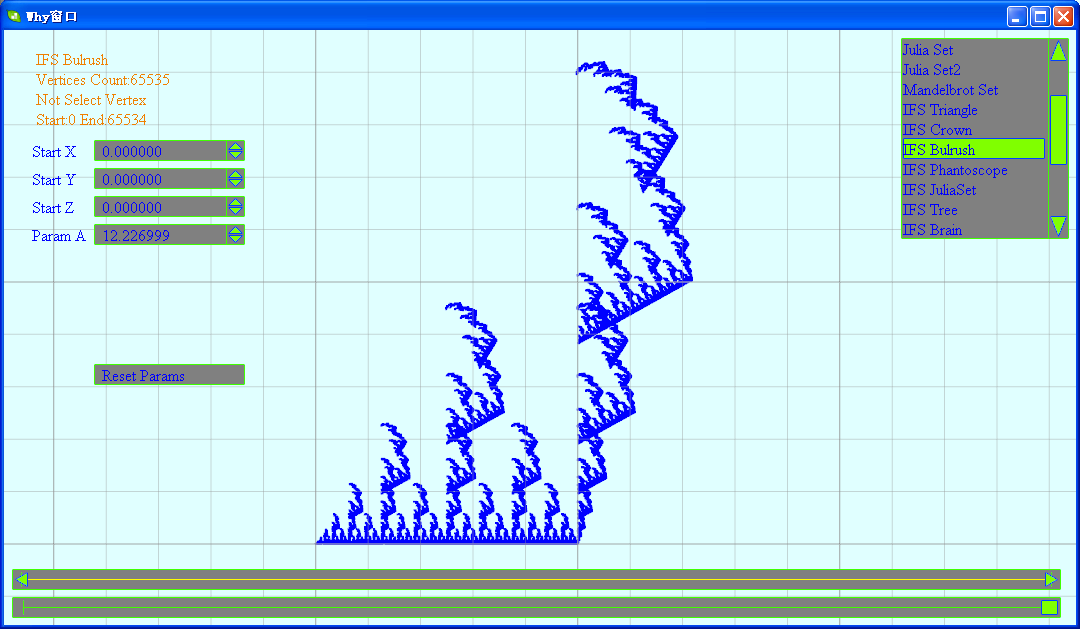
（3）芦苇

// 芦苇
class IFSBulrush : public FractalEquation
{
public:
    IFSBulrush()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = 10.0f;

        float k = m_ParamA*100.0f;

        //'IFS码赋值
        m[0][0] = 0.5f;  m[0][1] = 0.5f;  m[0][2] = 0;  m[0][3] = 0;  m[0][4] = 0;    m[0][5] = 0;        m[0][6] = 0.3f;
        m[1][0] = 0.5f;  m[1][1] = 0.5f;  m[1][2] = k;  m[1][3] = k;  m[1][4] = 1;    m[1][5] = k/1600;   m[1][6] = 0.3f;
        m[2][0] = 0.5f;  m[2][1] = 0.5f;  m[2][2] = 0;  m[2][3] = 0;  m[2][4] = 0.5f; m[2][5] = 0;        m[2][6] = 0.4f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float a, b, c, d, e, f;    //'仿射变幻中的系数

        float R = (float)rand()/RAND_MAX;

        if (R <= m[0][6]) 
        {
            a = m[0][0]; b = m[0][1]; c = m[0][2]; d = m[0][3]; e = m[0][4]; f = m[0][5];
        } 
        else if (R <= m[0][6] + m[1][6]) 
        {
            a = m[1][0]; b = m[1][1]; c = m[1][2]; d = m[1][3]; e = m[1][4]; f = m[1][5];
        } 
        else 
        {
            a = m[2][0]; b = m[2][1]; c = m[2][2]; d = m[2][3]; e = m[2][4]; f = m[2][5];
        } 

        outX = (a * x*cosf(c/180)) - (b * y*sinf(d/180)) + e*FRACTAL_RADIUS;
        outY = (a * x*sinf(c/180)) + (b * y*cosf(d/180)) + f*FRACTAL_RADIUS;
        outZ = z;
    }

    bool IsValidParamA() const {return true;}

    void SetParamA(float v)
    {
        m_ParamA = v;
        float k = m_ParamA*100.0f;
        m[1][2] = k;  
        m[1][3] = k;  
        m[1][5] = k/1600;
    }

private:
    float m[3][7];      // '存放IFS码
};

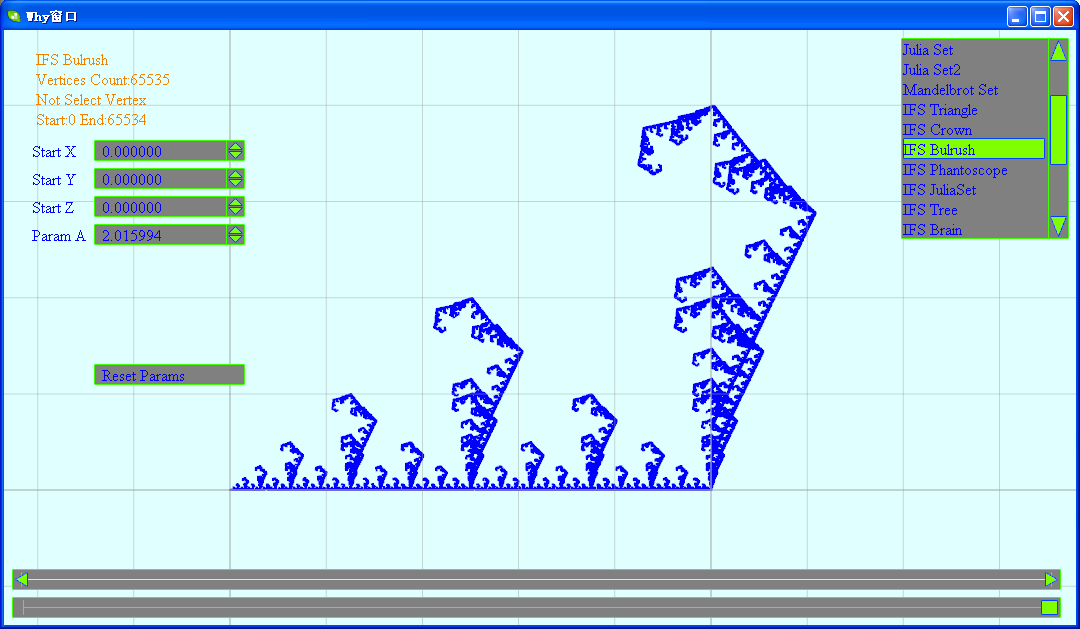
（4）万花筒

// 万花筒
class IFSPhantoscope : public FractalEquation
{
public:
    IFSPhantoscope()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = 2.0f;

        float k = m_ParamA*100.0f;

        //'IFS码赋值
        m[0][0] = 0.2f;  m[0][1] = 0.2f;  m[0][2] = 0;  m[0][3] = 0;  m[0][4] = 0.7f; m[0][5] = 0;     m[0][6] = 0.2f;
        m[1][0] = 0.2f;  m[1][1] = 0.2f;  m[1][2] = 0;  m[1][3] = 0;  m[1][4] =-0.7f; m[1][5] = 0;     m[1][6] = 0.2f;
        m[2][0] = 0.2f;  m[2][1] = 0.2f;  m[2][2] = 0;  m[2][3] = 0;  m[2][4] = 0;    m[2][5] = 0.7f;  m[2][6] = 0.2f;
        m[3][0] = 0.2f;  m[3][1] = 0.2f;  m[3][2] = 0;  m[3][3] = 0;  m[3][4] = 0;    m[3][5] = -0.7f; m[3][6] = 0.2f;
        m[4][0] = 0.85f; m[4][1] = 0.85f; m[4][2] = k;  m[4][3] = k;  m[4][4] = 0;    m[4][5] = 0;     m[4][6] = 0.2f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float a, b, c, d, e, f;    //'仿射变幻中的系数

        float R = (float)rand()/RAND_MAX;

        if (R <= m[0][6]) 
        {
            a = m[0][0]; b = m[0][1]; c = m[0][2]; d = m[0][3]; e = m[0][4]; f = m[0][5];
        } 
        else if (R <= m[0][6] + m[1][6]) 
        {
            a = m[1][0]; b = m[1][1]; c = m[1][2]; d = m[1][3]; e = m[1][4]; f = m[1][5];
        } 
        else if (R <= m[0][6] + m[1][6] + m[2][6]) 
        {
            a = m[2][0]; b = m[2][1]; c = m[2][2]; d = m[2][3]; e = m[2][4]; f = m[2][5];
        } 
        else if (R <= m[0][6] + m[1][6] + m[2][6] + m[3][6]) 
        {
            a = m[3][0]; b = m[3][1]; c = m[3][2]; d = m[3][3]; e = m[3][4]; f = m[3][5];
        } 
        else 
        {
            a = m[4][0]; b = m[4][1]; c = m[4][2]; d = m[4][3]; e = m[4][4]; f = m[4][5];
        }

        outX = (a * x*cosf(c/180)) - (b * y*sinf(d/180)) + e*FRACTAL_RADIUS;
        outY = (a * x*sinf(c/180)) + (b * y*cosf(d/180)) + f*FRACTAL_RADIUS;
        outZ = z;
    }

    bool IsValidParamA() const {return true;}

    void SetParamA(float v)
    {
        m_ParamA = v;
        float k = m_ParamA*100.0f;
        m[4][2] = k;  
        m[4][3] = k;
    }

private:
    float m[5][7];      // '存放IFS码
};

 

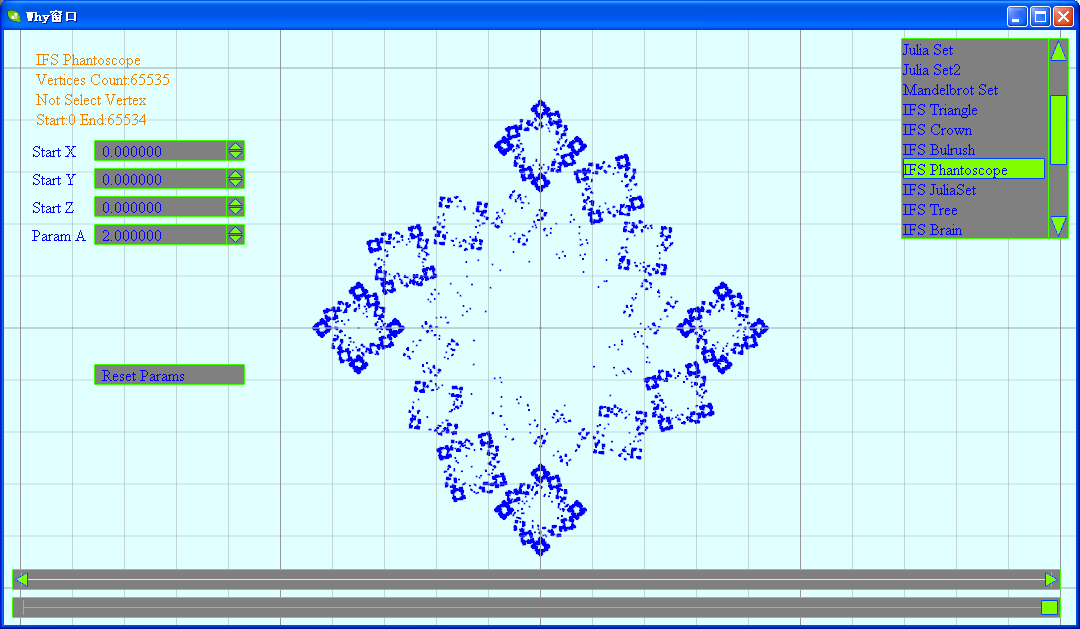
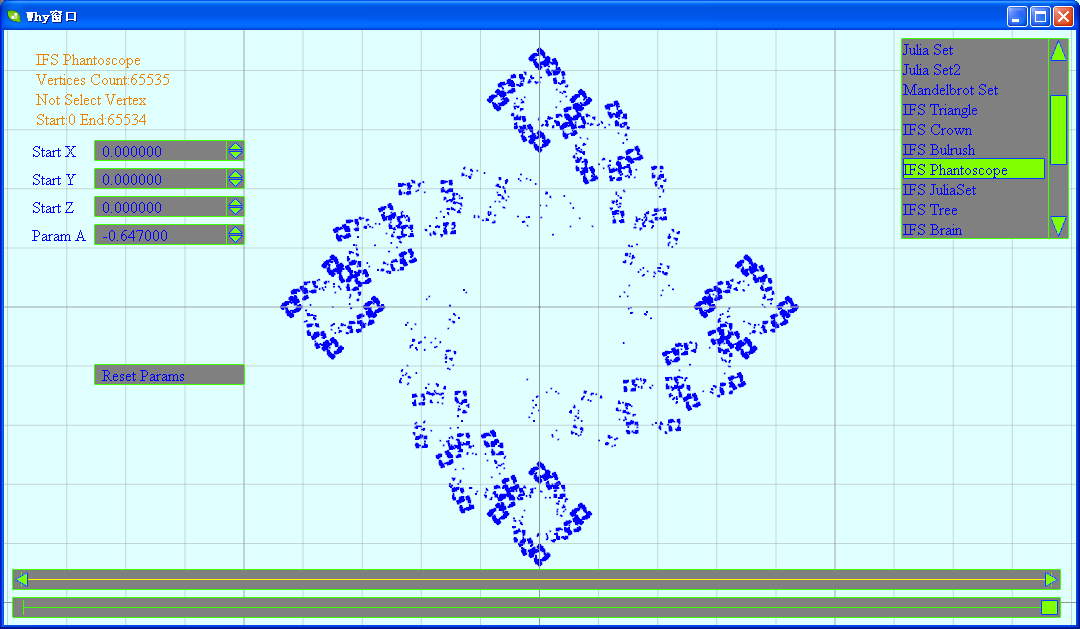
（5）Tree

class IFSTree : public FractalEquation
{
public:
    IFSTree()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        //'IFS码赋值
        m[0][0] = 0.195f;  m[0][1] =-0.488f; m[0][2] = 0.344f; m[0][3] = 0.433f; m[0][4] = 0.4431f; m[0][5] = 0.2452f; m[0][6] = 0.25f;
        m[1][0] = 0.462f;  m[1][1] = 0.414f; m[1][2] =-0.252f; m[1][3] = 0.361f; m[1][4] = 0.2511f; m[1][5] = 0.5692f; m[1][6] = 0.25f;
        m[2][0] =-0.058f;  m[2][1] =-0.07f;  m[2][2] = 0.453f; m[2][3] =-0.111f; m[2][4] = 0.5976f; m[2][5] = 0.0969f; m[2][6] = 0.25f;
        m[3][0] =-0.035f;  m[3][1] = 0.07f;  m[3][2] =-0.469f; m[3][3] =-0.022f; m[3][4] = 0.4884f; m[3][5] = 0.5069f; m[3][6] = 0.2f;
        m[4][0] =-0.637f;  m[4][1] = 0.0f;   m[4][2] = 0.0f;   m[4][3] = 0.501f; m[4][4] = 0.8562f; m[4][5] = 0.2513f; m[4][6] = 0.05f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float a, b, c, d, e, f;    //'仿射变幻中的系数

        float R = (float)rand()/RAND_MAX;

        if (R <= m[0][6]) 
        {
            a = m[0][0]; b = m[0][1]; c = m[0][2]; d = m[0][3]; e = m[0][4]; f = m[0][5];
        } 
        else if (R <= m[0][6] + m[1][6]) 
        {
            a = m[1][0]; b = m[1][1]; c = m[1][2]; d = m[1][3]; e = m[1][4]; f = m[1][5];
        } 
        else if (R <= m[0][6] + m[1][6] + m[2][6]) 
        {
            a = m[2][0]; b = m[2][1]; c = m[2][2]; d = m[2][3]; e = m[2][4]; f = m[2][5];
        } 
        else if (R <= m[0][6] + m[1][6] + m[2][6] + m[3][6]) 
        {
            a = m[3][0]; b = m[3][1]; c = m[3][2]; d = m[3][3]; e = m[3][4]; f = m[3][5];
        } 
        else 
        {
            a = m[4][0]; b = m[4][1]; c = m[4][2]; d = m[4][3]; e = m[4][4]; f = m[4][5];
        }

        outX = a*x + b*y + e;
        outY = c*x + d*y + f;
        outZ = z;
    }

private:
    float m[5][7];      // '存放IFS码
};

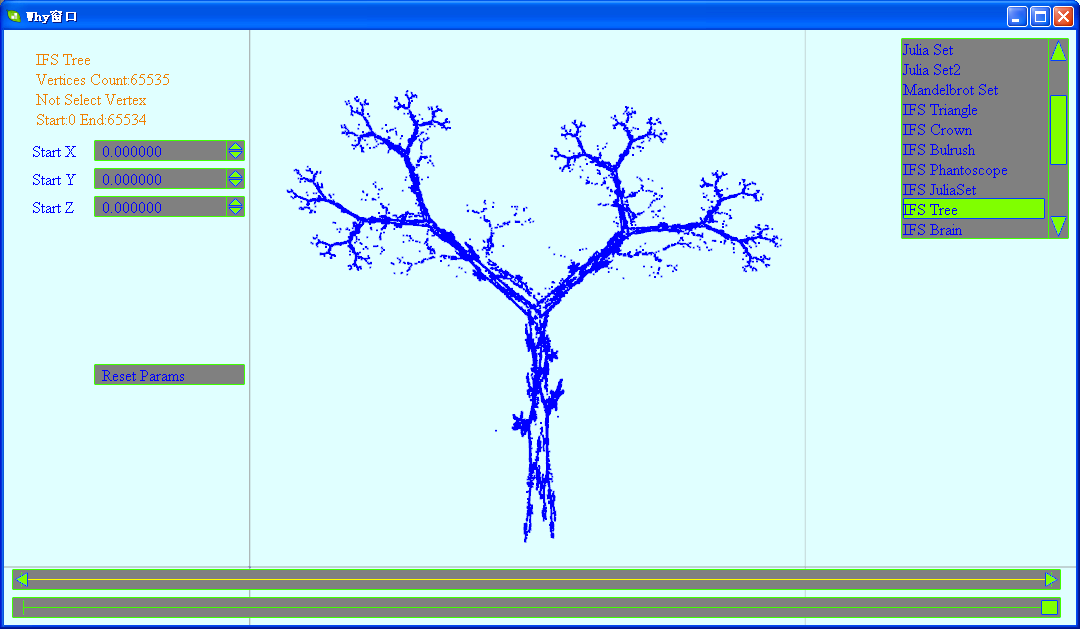
这个图形我很喜欢，所以还专门将其生成图像：

（6）大脑

class IFSBrain : public FractalEquation
{
public:
    IFSBrain()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        //'IFS码赋值
        //0.03  0       0       0.45    0   0     0.05;    
        //-0.03 0       0       -0.45   0   0.4   0.15;    
        //0.56  -0.56   0.56    0.56    0   0.4   0.4;      
        //0.56  0.56    -0.56   0.56    0   0.4   0.4;
        m[0][0] = 0.03f;  m[0][1] = 0.0f;   m[0][2] = 0.0f;  m[0][3] = 0.45f; m[0][4] = 0.0f; m[0][5] = 0.0f; m[0][6] = 0.05f;
        m[1][0] =-0.03f;  m[1][1] = 0.0f;   m[1][2] = 0.0f;  m[1][3] =-0.45f; m[1][4] = 0.0f; m[1][5] = 0.4f; m[1][6] = 0.15f;
        m[2][0] = 0.56f;  m[2][1] =-0.56f;  m[2][2] = 0.56f; m[2][3] = 0.56f; m[2][4] = 0.0f; m[2][5] = 0.4f; m[2][6] = 0.4f;
        m[3][0] = 0.56f;  m[3][1] = 0.56f;  m[3][2] =-0.56f; m[3][3] = 0.56f; m[3][4] = 0.0f; m[3][5] = 0.4f; m[3][6] = 0.4f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float a, b, c, d, e, f;    //'仿射变幻中的系数

        float R = (float)rand()/RAND_MAX;

        if (R <= m[0][6]) 
        {
            a = m[0][0]; b = m[0][1]; c = m[0][2]; d = m[0][3]; e = m[0][4]; f = m[0][5];
        } 
        else if (R <= m[0][6] + m[1][6]) 
        {
            a = m[1][0]; b = m[1][1]; c = m[1][2]; d = m[1][3]; e = m[1][4]; f = m[1][5];
        } 
        else if (R <= m[0][6] + m[1][6] + m[2][6]) 
        {
            a = m[2][0]; b = m[2][1]; c = m[2][2]; d = m[2][3]; e = m[2][4]; f = m[2][5];
        } 
        else
        {
            a = m[3][0]; b = m[3][1]; c = m[3][2]; d = m[3][3]; e = m[3][4]; f = m[3][5];
        } 

        outX = a*x + b*y + e;
        outY = c*x + d*y + f;
        outZ = z;
    }

private:
    float m[4][7];      // '存放IFS码
};

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

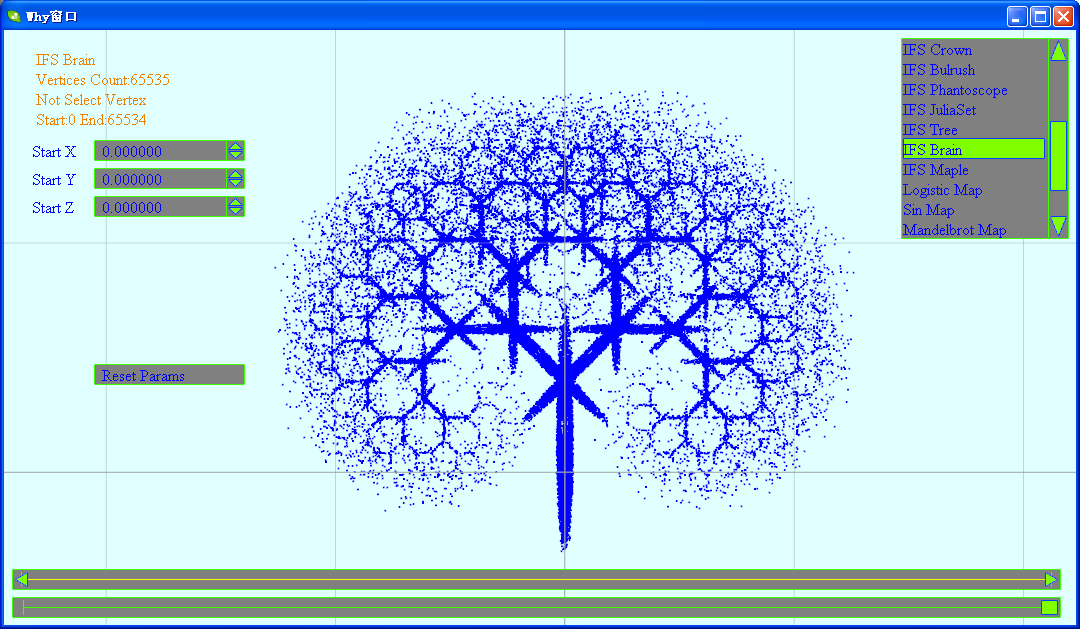
关于基类FractalEquation的定义及相关软件见：混沌与分形

最后

以上就是自然大碗为你收集整理的混沌分形之迭代函数系统（IFS）的全部内容，希望文章能够帮你解决混沌分形之迭代函数系统（IFS）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(45)

相关文章

迭代函数系统matlab实现,使用MATLAB实现随机分形树模拟
迭代函数系统matlab实现,使用MATLAB实现随机分形树模拟
强化学习经典算法笔记(一)：价值迭代算法Value Iteration强化学习经典算法笔记——价值迭代算法
强化学习经典算法笔记(一)：价值迭代算法Value Iteration强化学习经典算法笔记——价值迭代算法
Python核心编程三大神兽——迭代器、生成器 、以及装饰器
Python核心编程三大神兽——迭代器、生成器 、以及装饰器
matlab portfolio函数,Portfolio Optimization Examples
matlab portfolio函数,Portfolio Optimization Examples
混沌分形之迭代函数系统（IFS）
混沌分形之迭代函数系统（IFS）
变步长梯形法求积分matlab程序,变步长复化辛普森公式计算积分
变步长梯形法求积分matlab程序,变步长复化辛普森公式计算积分
matlab里的仿真模型块,搭建simulink模型（如何利用MATLAB/SIMULINK搭建简单的仿真模型）...
matlab里的仿真模型块,搭建simulink模型（如何利用MATLAB/SIMULINK搭建简单的仿真模型）...
Simulink仿真踩坑
Simulink仿真踩坑

评论列表共有 0 条评论

立即
投稿
返回
顶部