强化学习经典算法笔记——价值迭代算法
由于毕业设计做的是强化学习相关的内容,感觉有必要把强化学习经典算法实现一遍,加强对算法和编程的理解。所以从这一篇开始,每一篇实现一个算法,主要包括Value Iteration,Policy Iteration,Q Learning,Actor-Critic算法及其衍生的DDPG等。期间还会在代码中介绍OpenAI Gym中的游戏环境。
强化学习的基本概念不再赘述,可以参考《深入浅出强化学习:原理入门》。
正文开始。
简单介绍
对于简单的强化学习问题,可以用马尔科夫决策过程(Markov Decision Process,MDP)来建模。通过引入Value Function和Q Function,可以推导出用以解决MDP问题的贝尔曼方程:
V ∗ ( s ) = m a x a ∑ s ′ P s s ′ a [ R s s ′ a + γ ∑ a ′ Q π ( s ′ , a ′ ) ] V^*(s) = max_a sum_{s'} P_{ss'}^{a}[ R_{ss'}^a + gamma sum_{a'}Q^{pi}(s',a') ] V∗(s)=maxas′∑Pss′a[Rss′a+γa′∑Qπ(s′,a′)]
对于贝尔曼方程的求解,可以采取动态规划(Dynamic Programming)的方法。具体来说,动态规划有两个方法:
- 价值迭代 Value Iteration
- 策略迭代 Policy Iteration
本篇主要介绍Value Iteration,值迭代。
算法主要流程如下。
- 初始化Value Function,即对每个状态的价值都赋一个初始值,一般是0
- 计算每一个状态-动作pair 的值,也就是 Q ( s , a ) Q(s,a) Q(s,a)
- 每一个状态 s t s_t st下都有一个动作空间 a t ∈ A a_t in A at∈A,选 m a x a t Q ( s t , a t ) max_{a_t} Q(s_t,a_t) maxat Q(st,at),即最大的Q值作为当前状态的价值,更新Value Function
- 返回第2步,直至Value Function收敛。
编程实现
下面用一个Gym里的小游戏FrozenLake实现值迭代算法。FrozenLake是一个状态空间完全可见,状态之间的转移规律也比较清晰的有模型可依的MDP问题,很适合用值迭代算法来求解。
FrozenLake游戏的状态空间很简单,是一个 4 × 4 4times4 4×4的矩阵,每个位置有一个字母:
- S,Starting Point,起始位置,安全
- F,Frozen Surface,冻结的湖面,安全
- H,Hole,洞,来到这个位置游戏失败,得-1分
- G,Goal,游戏终点,来到这个位置,得1分
SFFF
FHFH
FFFH
HFFG
游戏的动作空间也很简单。只有四个option,分别是0,1,2,3,代表朝四个方向运动。当然,游戏中向左运动的命令不一定100%被执行,而是有一定概率“被风吹到”其他地方,增加了游戏的随机性。
3
^
|
0< —— o —— > 2
|
v
1
需要注意的是,在左侧边界(矩阵的最左列)是没法向左移动的,有一定概率(较大)保持原地,有较小概率向下移动;在上侧边缘(矩阵的第一行)没法向上走,较大概率原地不动,较小概率向右移动,右侧和下侧亦然。
在最后收敛的policy中,我们可以看到,agent很聪明地利用了这个特点来达到最后的目的地。
首先导入必要的package。
import gym
import numpy as np
env = gym.make('FrozenLake-v0')
env.reset() # 初始化游戏环境
编写价值迭代函数主体,代码中给了详细的注释,在这里就不多解释了。
def value_iteration(env, gamma = 0.8, no_of_iterations = 2000):
'''
值迭代函数,目的是准确评估每一个状态的好坏
'''
# 状态价值函数,向量维度等于游戏状态的个数
value_table = np.zeros(env.observation_space.n)
threshold = 1e-20
for i in range(no_of_iterations):
updated_value_table = np.copy(value_table)
for state in range(env.observation_space.n): # state = 0,1,2,3,...,15
# 在某个状态下,采取4种动作后,分别的reward,Q_value长度=4
Q_value = []
for action in range(env.action_space.n): # action = 0,1,2,3
# 采取不同action转移到不同的状态,也对应不同的reward
next_states_rewards = []
for next_sr in env.P[state][action]: # 在当前state和action的情况下,把可能转移的状态遍历一遍
# next_sr = (0.3333333333333333, 8, 0.0 , False)
# next_sr = (状态转移概率, 下一个状态,得到reward的概率,游戏是否结束)
trans_prob, next_state, reward_prob, _ = next_sr
# 下一状态t的动作状态价值 = 转移到t状态的概率 × ( env反馈的reward + γ × t状态的当前价值 )
next_states_rewards.append((trans_prob * (reward_prob + gamma * updated_value_table[next_state])))
# 将某一动作执行后,所有可能的t+1状态的价值加起来,就是在t状态采取a动作的价值
Q_value.append(np.sum(next_states_rewards))
# Q_value长度为4(上下左右),选Q_value的最大值作为该状态的价值
value_table[state] = max(Q_value)
# 如果状态价值函数已经收敛
if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
print ('Value-iteration converged at iteration# %d.' %(i+1))
break
return value_table
等到Value Function收敛之后,也就是说,我们认为Value Function可以很好地估计每一个游戏状态是好是坏了。这时遍历每个状态,把当前状态下,具有最高价值的动作选出来,以后每次来到这个状态,就执行这个动作。因此我们编写一个extract_policy函数。
def extract_policy(value_table, gamma = 1.0):
'''
在一个收敛的、能够对状态进行准确评估的状态值函数的基础上,推导出策略函数,即在每一个状态下应该采取什么动作最优的
'''
# policy代表处于状态t时应该采取的最佳动作是上/下/左/右,policy长度16
policy = np.zeros(env.observation_space.n)
for state in range(env.observation_space.n):
# 将价值迭代的过程再走一遍,但是不再更新value function,而是选出每个状态下对应最大价值的动作
Q_table = np.zeros(env.action_space.n) # len=4
for action in range(env.action_space.n):
for next_sr in env.P[state][action]:
#
trans_prob, next_state, reward_prob, _ = next_sr
#
Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
# 选最优价值的动作
policy[state] = np.argmax(Q_table)
return policy
最后依次执行两个函数,得到收敛后的最优策略。
optimal_value_function = value_iteration(env=env)
print('nthe best value function:n',optimal_value_function,'n')
optimal_policy = extract_policy(optimal_value_function, gamma=1.0)
print('the best policy:n',optimal_policy)
输出结果:
Value-iteration converged at iteration# 148.
the best value function:
[0.01543434 0.0155907 0.0274401 0.01568006 0.02685373 0.
0.05978021 0. 0.05841341 0.13378315 0.1967357 0.
0. 0.2465377 0.54419553 0. ]
the best policy:
[1. 3. 2. 3. 0. 0. 0. 0. 3. 1. 0. 0. 0. 2. 1. 0.]
完整代码如下。
import gym
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 0 -> 左
# 1 -> 下
# 2 -> 右
# 3 -> 上
# 3
# ^
# |
# 0< —— o —— > 2
# |
# v
# 1
# 动作空间=4,分别是上下左右移动,同时湖面上可能刮风,使agent随机移动
# S Starting point,safe
# F Frozen surface,safe
# H Hole,end of game,bad
# G Goal,end of game,good
# 状态空间=16,4x4的矩阵
# SFFF
# FHFH
# FFFH
# HFFG
# 在左侧边缘,无法向左移动,要么原地不动,要么向下移动
# 在上侧边缘,无法向上移动,要么原地不动,要么向右移动
env = gym.make('FrozenLake-v0')
env.reset()
def value_iteration(env, gamma = 1.0, no_of_iterations = 2000):
'''
值迭代函数,目的是准确评估每一个状态的好坏
'''
# 状态价值函数,向量维度等于游戏状态的个数
value_table = np.zeros(env.observation_space.n)
# 随着迭代,记录算法的收敛性
error = [] # 价值函数的差
index = [] # 价值函数的第一个元素
threshold = 1e-20
for i in range(no_of_iterations):
updated_value_table = np.copy(value_table)
for state in range(env.observation_space.n): # state = 0,1,2,3,...,15
# 在某个状态下,采取4种动作后,分别的reward,Q_value长度=4
Q_value = []
for action in range(env.action_space.n): # action = 0,1,2,3
# 采取不同action转移到不同的状态,也对应不同的reward
next_states_rewards = []
for next_sr in env.P[state][action]: # 在当前state和action的情况下,把可能转移的状态遍历一遍
# next_sr = (0.3333333333333333, 8, 0.0 , False)
# next_sr = (状态转移概率, 下一个状态,得到reward的概率,游戏是否结束)
trans_prob, next_state, reward_prob, _ = next_sr
# 下一状态t的动作状态价值 = 转移到t状态的概率 × ( env反馈的reward + γ × t状态的当前价值 )
next_states_rewards.append((trans_prob * (reward_prob + gamma * updated_value_table[next_state])))
# 将某一动作执行后,所有可能的t+1状态的价值加起来,就是在t状态采取a动作的价值
Q_value.append(np.sum(next_states_rewards))
# Q_value长度为4(上下左右),选Q_value的最大值作为该状态的价值
value_table[state] = max(Q_value)
index.append(value_table[0])
# 如果状态价值函数已经收敛
error.append(np.sum(np.fabs(updated_value_table - value_table)))
if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
print ('Value-iteration converged at iteration# %d.' %(i+1))
break
# 画出价值函数的收敛曲线
plt.figure(1)
plt.plot(error)
# 画出价值函数第一个元素的值的收敛情况
plt.figure(2)
plt.plot(index)
return value_table
def extract_policy(value_table, gamma = 1.0):
'''
在一个收敛的、能够对状态进行准确评估的状态值函数的基础上,推导出策略函数,即在每一个状态下应该采取什么动作最优的
'''
# policy代表处于状态t时应该采取的最佳动作是上/下/左/右,policy长度16
policy = np.zeros(env.observation_space.n)
for state in range(env.observation_space.n):
# 将价值迭代的过程再走一遍,但是不再更新value function,而是选出每个状态下对应最大价值的动作
Q_table = np.zeros(env.action_space.n) # len=4
for action in range(env.action_space.n):
for next_sr in env.P[state][action]:
#
trans_prob, next_state, reward_prob, _ = next_sr
#
Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
# 选最优价值的动作
policy[state] = np.argmax(Q_table)
return policy
optimal_value_function = value_iteration(env=env)
print('nthe best value function:n',optimal_value_function,'n')
optimal_policy = extract_policy(optimal_value_function, gamma=1.0)
print('the best policy:n',optimal_policy)
下图是经过1373次迭代,新旧value table之差的收敛情况。
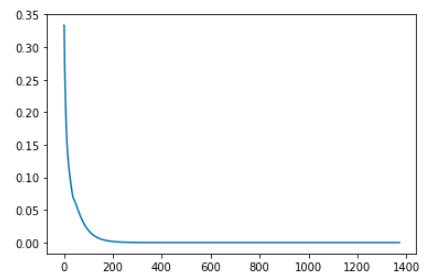
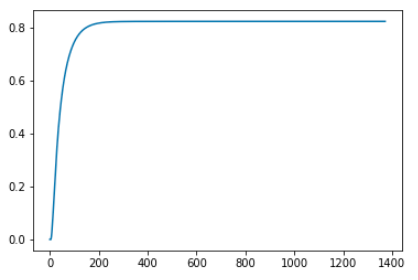
这张图是对value table的第一个元素,也就是第一个状态的价值,在1373次迭代过程中的变化情况。两张图都显示了算法已经收敛。
将16个状态的最终价值列出来,会发现算法对安全和危险的地方是有基本的判断的,体现在状态价值上就是,靠近H的地方相应的价值也就低,H价值为0。
0.82352941 0.82352941 0.82352941 0.82352941
0.82352941 0. 0.52941176 0.
0.82352941 0.82352941 0.76470588 0.
0. 0.88235294 0.94117647 0.
对应于
SFFF
FHFH
FFFH
HFFG
最后
以上就是忧郁钻石最近收集整理的关于强化学习经典算法笔记(一):价值迭代算法Value Iteration强化学习经典算法笔记——价值迭代算法的全部内容,更多相关强化学习经典算法笔记(一):价值迭代算法Value内容请搜索靠谱客的其他文章。








发表评论 取消回复