设计时序逻辑电路
功能要求:用JK触发器和逻辑门设计一个七进制的同步加法计数器
首先分析题目,可以知道七进制计数器有7个不同的状态,需要3个触发器(触发器有两个状态)
2
3
≥
7
2^3 ge 7
23≥7
第一步 状态转换图
得到计数器输出端
Q
2
,
Q
1
,
Q
0
Q2,Q1,Q0
Q2,Q1,Q0的状态转换图如下所示: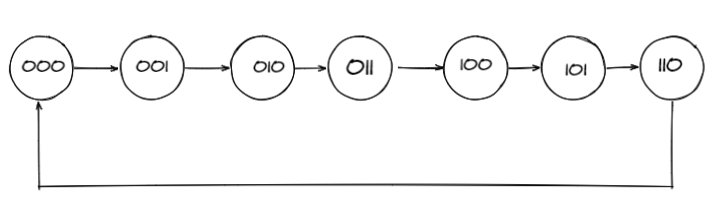
第二步 次态转换图
-
总的次态转换图如下所示:
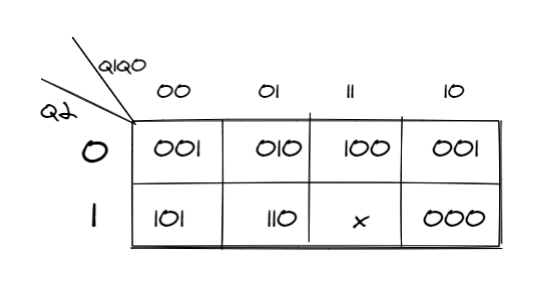
-
各位输出分卡诺图如下所示:
-
Q
0
Q_0
Q0的次态
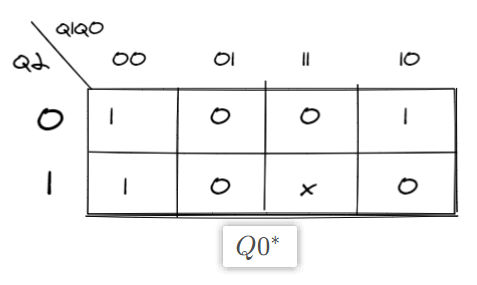
-
Q
1
的
次
态
Q1的次态
Q1的次态
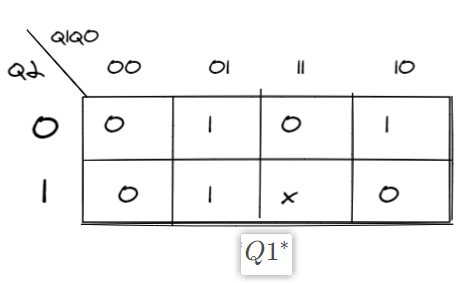
-
Q
2
Q2
Q2的次态
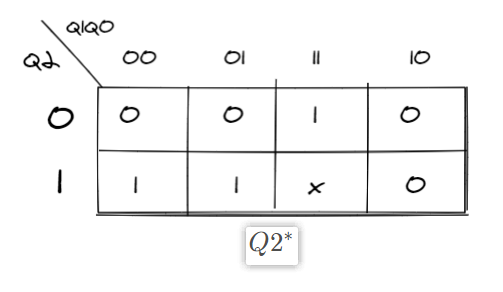
-
Q
0
Q_0
Q0的次态
第三步 状态方程
写状态方程时重点在于我们使用的是JK触发器,所以有意的写成JK触发器特性方程的形式
ps:JK触发器相关知识复习点击此处跳转
- Q 0 n + 1 = Q 1 n ‾ Q 0 n ‾ + Q 2 n ‾ Q 0 n ‾ = Q 2 n ‾ Q 1 n ‾ Q 0 n ‾ = Q 2 n ‾ Q 1 n ‾ ⋅ Q 0 n ‾ = Q 2 n ‾ Q 1 n ‾ ⋅ Q 0 n ‾ + 0 ⋅ Q 0 n Q_0^{n+1}=overline{{Q_1^{n}}} overline{{Q_0^{n}}}+overline{{Q_2^{n}}} overline{{Q_0^{n}}}=overline{{Q_2^{n}}} overline{{Q_1^{n}}} overline{{Q_0^{n}}}=overline{{Q_2^{n}}}overline{{Q_1^{n}}} cdot overline{{Q_0^{n}}}=overline{{Q_2^{n}}}overline{{Q_1^{n}}}cdot overline{{Q_0^{n}}}+0cdot {{Q_0^{n}}} Q0n+1=Q1n Q0n+Q2n Q0n=Q2n Q1n Q0n=Q2nQ1n⋅Q0n=Q2nQ1n⋅Q0n+0⋅Q0n
- Q 1 n + 1 = Q 0 n ⋅ Q 1 n ‾ + Q 2 n ‾ Q 0 n ‾ ⋅ Q 1 n ‾ Q_1^{n+1}={{Q_0^{n}}}cdot overline{{Q_1^{n}}}+overline{{Q_2^{n}}} overline{{Q_0^{n}}}cdotoverline{{Q_1^{n}}} Q1n+1=Q0n⋅Q1n+Q2n Q0n⋅Q1n
- Q 2 n + 1 = Q 1 n Q 0 n ⋅ Q 2 n ‾ + Q 1 n ‾ ⋅ Q 2 n Q_2^{n+1}={{Q_1^{n}}}{{Q_0^{n}}}cdot overline{{Q_2^{n}}}+ overline{{Q_1^{n}}}cdot {{Q_2^{n}}} Q2n+1=Q1nQ0n⋅Q2n+ Q1n⋅Q2n
第四步 驱动方程
根据三个触发器的状态方程,和采用的JK触发器特性方程联合(注:
Q
n
+
1
=
J
Q
n
+
K
′
Q
n
Q^{n+1}=JQ^n+K'Q^n
Qn+1=JQn+K′Qn),求出相应的驱动方程
J
0
=
Q
2
n
Q
1
n
‾
K
0
′
=
0
⇒
K
0
=
1
J_0=overline{{{Q_2^n}}{{Q_1^{n}}} }qquad K_0'=0Rightarrow K_0=1
J0=Q2nQ1nK0′=0⇒K0=1
J
1
=
Q
0
n
K
1
=
Q
2
n
‾
Q
0
n
‾
‾
J_1={{Q_0^{n}}} qquad K_1=overline{overline{{{Q_2^{n}}}} overline{{{Q_0^{n}}}}}
J1=Q0nK1=Q2n Q0n
J
2
=
Q
1
n
Q
0
n
K
2
=
Q
1
n
J_2={{Q_1^n}}{{Q_0^{n}}} qquad K_2={{Q_1^{n}}}
J2=Q1nQ0nK2=Q1n
第五步 根据驱动方程画电路图
根据驱动方程画出电路图如下所示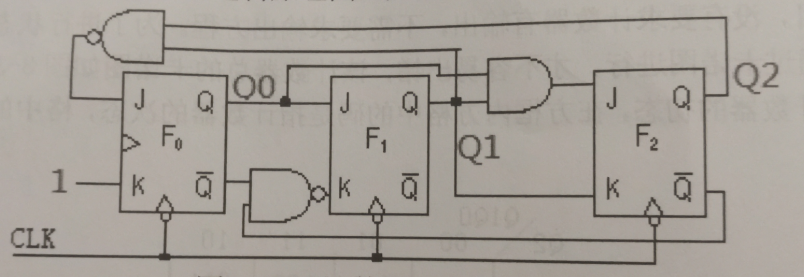
第六步 检查自启动
检查自启动先检查状态转换图的无效状态码"“111"”,接下来将这个码作为电路的初始状态代入,发现’’‘111’’'的次态是"“000"”,000正好是状态循环圈中的一部分。
所以电路能够自启动。
下面是自启动状态转换图: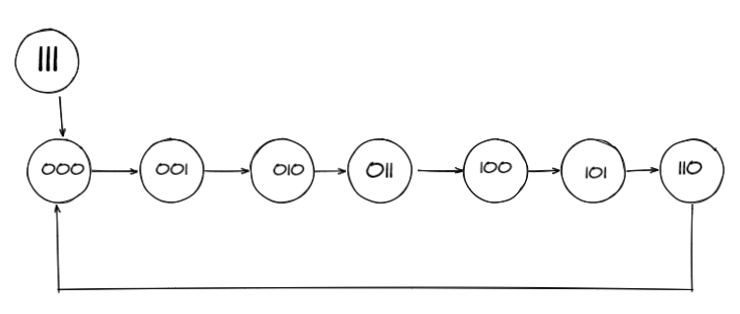
时序逻辑电路的设计这样就结束啦!
最后
以上就是壮观柠檬最近收集整理的关于时序逻辑电路设计方法和步骤设计时序逻辑电路的全部内容,更多相关时序逻辑电路设计方法和步骤设计时序逻辑电路内容请搜索靠谱客的其他文章。








发表评论 取消回复