我是靠谱客的博主 活力画板,这篇文章主要介绍Python关于频谱图以及功率谱密度纵坐标和原振动加速度之间的关系首先是关于快速傅里叶变换的 然后是功率谱密度的(周期图法),现在分享给大家,希望可以做个参考。
首先是关于快速傅里叶变换的
x = np.arange(0, 1, 1/1400)
#设置需要采样的信号,频率分量有200,400和600
S=7*np.sin(2*np.pi*200*x) + 5*np.sin(2*np.pi*400*x)+3*np.sin(2*np.pi*600*x)
y_1 = S
T=1/1400
t = [i*T for i in range(len(y_1))]
t = np.array(t)
complex_array = fft.fft(y_1)
plt.figure(figsize=(20, 20))
plt.subplot(211)
plt.grid(linestyle=':')
plt.plot(t, y_1, label='S') # y是1000个相加后的正弦序列
plt.xlabel("t(毫秒)")
plt.ylabel("S(t)幅值")
plt.legend()
plt.figure(figsize=(20, 20))
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅(能量大小)
pows = np.abs(complex_array)
plt.subplot(212)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()
#峰值的直流分量为除以N,后面的都是除以N/2,分辨率等于Fs/N,Fn=(n-1)*Fs/N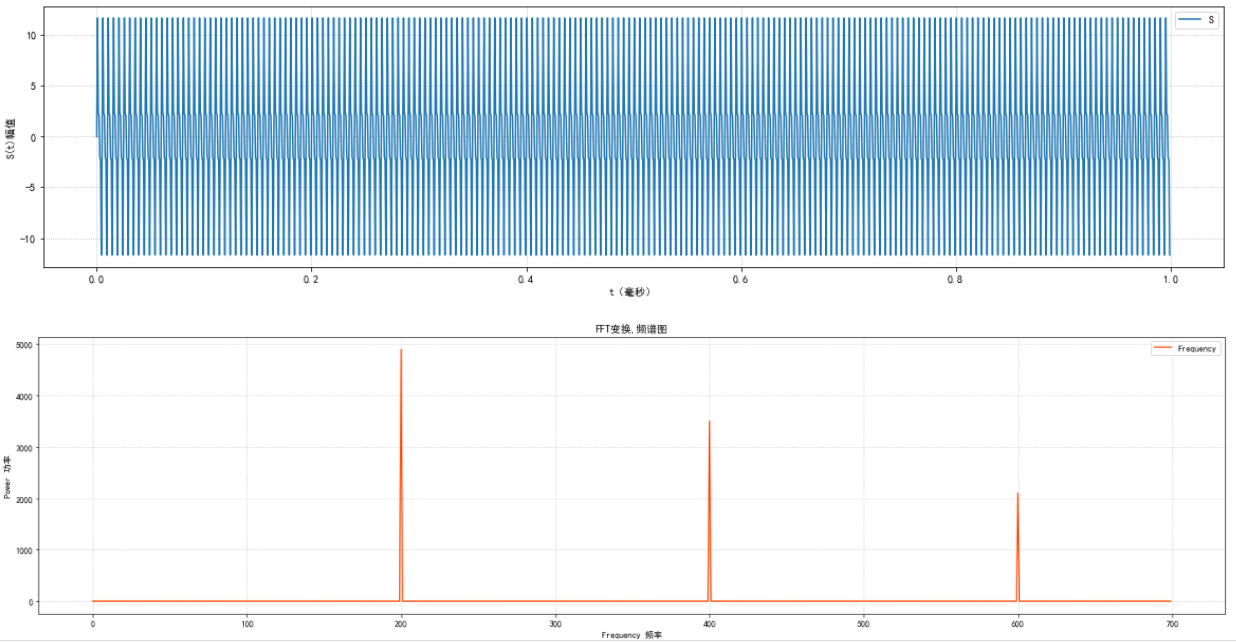
比如这个变换,对应200Hz的的功率为4900w,4900/(N/2)=4900/(1400/2)=7,刚好也就对了
第一个峰值(频率位置)的模是A1的N倍,N为采样点,本例中为N=1400,此例中没有,因为信号没有常数项A1
第二个峰值(频率位置)的模是A2的N/2倍,N为采样点,
第三个峰值(频率位置)的模是A3的N/2倍,N为采样点,
第四个峰值(频率位置)的模是A4的N/2倍,N为采样点,详见使用python(scipy和numpy)实现快速傅里叶变换(FFT)最详细教程_MIss-Y的博客-CSDN博客
然后是功率谱密度的(周期图法)
我同时用fft和周期图法做了一个频谱分析
fs=1000;
N=1000;
n=np.arange(1000);
t=n/fs;
x=np.sin(2*np.pi*100*t);
#直接法,periodogram函数得到的功率谱密度
[Pxx_period,f_period]=periodogram(x,fs=1000);
plt.subplot(211)
plt.plot(Pxx_period, f_period)
y_1 = x
T=1/1000
t = [i*T for i in range(len(x))]
t = np.array(t)
complex_array = fft.fft(y_1)
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅(能量大小)
pows = np.abs(complex_array)
plt.subplot(212)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()结果如下
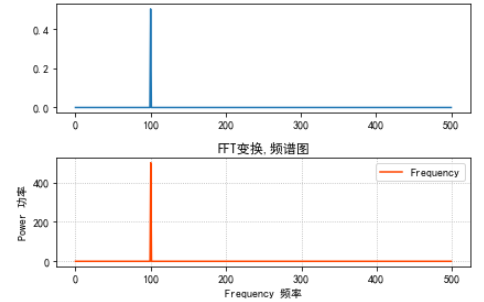
0.5*1000=500^2/500,也就是功率谱密度乘以fs得到功率谱。这个功率谱的图与对信号做fft后取信号模方除以N/2的图比较,这就是两者的转换关系,可以再举一个例子
fs = 10e3
N = 1e5
amp = 2
freq = 1234.0
time = np.arange(N) / fs
x = amp*np.sin(2*np.pi*freq*time)
f, Pxx_den = signal.periodogram(x, fs)
plt.subplot(211)
plt.plot(f, Pxx_den)
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
y_1 = x
T=1/10000
t = [i*T for i in range(len(x))]
t = np.array(t)
complex_array = fft.fft(y_1)
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅(能量大小)
pows = np.abs(complex_array)
plt.subplot(212)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()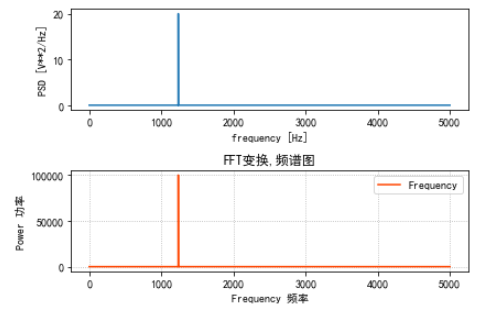
fs = 10000,N=100000,fft峰值为100000,周期图为20,可以计算100000^2/50000 = 20*10000可以看到刚好相等,也就是满足这么一个关系,然后我们再利用fft与加速度之间的关系,我们就可以得到一个功率谱密度的峰值与加速度之间的关系,
功率谱密度 = 加速度的平方*N/2再除以fs
功率谱密度的分辨率等于fs/N,个数为N/2+1个,应该是因为是单边谱的原因
fft的分辨率等于fs/N
最后
以上就是活力画板最近收集整理的关于Python关于频谱图以及功率谱密度纵坐标和原振动加速度之间的关系首先是关于快速傅里叶变换的 然后是功率谱密度的(周期图法)的全部内容,更多相关Python关于频谱图以及功率谱密度纵坐标和原振动加速度之间内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复