matlab自相关函数autocorr_随机过程的自相关函数与功率谱（转载）

100 阅读 0 评论 66 点赞

我是靠谱客的博主坚强樱桃，最近开发中收集的这篇文章主要介绍matlab自相关函数autocorr_随机过程的自相关函数与功率谱（转载），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

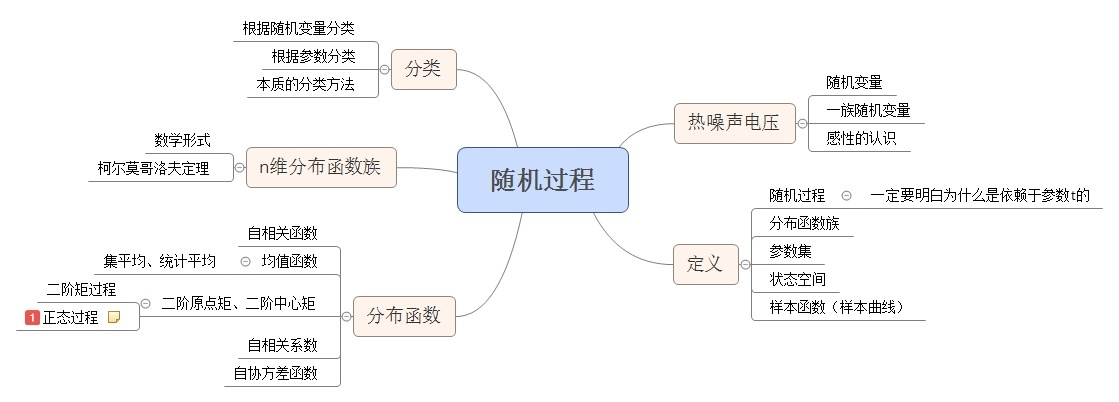
随机过程的自相关函数与功率谱

1. 自相关函数

要说自相关函数，这里得先从统计里的相关函数定义讲起。在统计里，两个随机变量X，Y的相关函数定义如下：

也就是两个随机变量协方差除以标准差之积。如果

X是一个时间的随机变量序列，将不同时间起始点的两个序列 Xt和 Xs看成两个随机变量，上面的相关函数（1）可以表示为：

如果

X是一个二阶稳态过程，即均值和方差不随时间变化。（这里涉及到随机过程的定义，可以去搜一下纯随机过程，平稳随机过程）

此时，相关函数只是时间差τ=s-t的函数，则公式（2）可以重写为：

这是统计学上的相关函数。

我们把式（4）中期望展开来看，也就是当随机序列有样本时：

上式其实是两个向量的内积表达式，即：

事实上，自相关函数在统计上，反映了同一随机序列在不同时刻取值之间的相关程度。而在信号处理中，一个向量的自相关函数以卷积的形式表达：

其中，当是

复函数时，

是

的复共轭。当

是实函数时，

。

可以看出和统计中的形式相似，所以信号处理中的自相关函数，同样反映的是同一个信号在不同时刻取值间的相关程度。若信号呈周期性，则当

取相应的的周期值时，自相关函数可以去的最大值。因此，可以通过自相关函数来分析信号的周期性。

在图像处理中，常应用到的是标准化互相关函数（Normalized Cross-Correlation，NCC）。比如，NCC在图像模板模板匹配时可用于度量匹配距离。 NCC表达形式，或本质和统计里的相关函数一致。

当有

，

两幅图像，如果其均值和方差分别为

和

,NCC为:

图像减掉均值，就具有了亮度不变性，然后在除以标准差，就具有了对比度不变性，就是说NCC度量距离具有在亮度和对比度变化下的稳定性。

2. 功率谱

功率谱有时也称为能量谱（power spectrum），或又称为功率密度谱（power density spectrum）或谱密度（spectral density 或power spectral density）

如果一个信号的功率谱为

，则该信号的总能量为

，其中

为信号的频率。

即对所有频率下的能量积分（或求和），就是信号的总能量。从这里也可以看出，功率谱表达的是信号某个频率下所拥有的能量。事实上，功率谱和直方图有很大的想私信。当直方图用于统计一个信号，每个频率区间中的能量时，其意义就和功率谱一致。

如何计算信号的功率谱呢？维纳-辛钦定理（Wiener-KhinchineTheorem）给出了一种计算方法，用文字表述，一个信号的功率谱密度就是该信号相关函数的傅里叶变换：

其中

是信号

的傅里叶变换，

是

的复共轭。

所以，当知道一个信号的傅里叶变换时，也可以直接求出该信号的功率谱。

至于维纳辛钦定理的证明，这里贴一个网上的版本。

3. 白噪声

有了功率谱的概念，就可以谈谈白噪音（White noise）了。

每个信号f(t)只有唯一的功率谱，虽然反过来未必成立。但功率谱是信号的一种属性。有这种属性，再加上别的一些属性，就可以用于区分信号了。比如在图像处理里，将图像函数看做一个信号函数，对图像某一区块其进行上述标准化互相关函数中讲到的亮度和对比度不变性处理后，进行傅里叶变换，并最后算出图像功率谱，于是就有了一个很好的以频率表达的可用于模板匹配的模板属性。这就是图像处理中所说的，把对图像处理的时空域内思考，转化到频域。可以使一些在时空域较难处理的问题，在频域里找到直观简便的解决方案。

白噪声（这里白噪声的解释可以参见百度百科），是一种功率谱密度为常数的随机信号或随机过程。功率谱密度为常数，也就是说，信号在各个频率上的能量相同。由于白光是不同频率的各色光混杂而成，所以同样在不同频率下具有相等能量的噪音被称为“白”的。

但是功率谱密度为常数又说明了什么呢？

如上所述，功率谱可由自相关函数的傅里叶变换得到。自相关函数可以反映一个函数的周期性。那么自相关函数经傅里叶变换后的功率谱也一样。而且，周期和频率原本就是一回事。如果某函数的频率谱在某个频率下取得很大的值，那么说明此函数具有一定的周期性。而对于白噪声而言，频率谱在所有频率下取值相同，就是说能量和频率没有关系，也就是说，能量和周期没有关系。所以白噪声不具有周期性。

既然自相关函数已经可以表达这个意思了，为什么还要再傅里叶变换一下，来表达同一个意思？事实上，从上面维纳-辛钦定理可以看出，信号的频率谱可以直接由信号的傅里叶变换得到，而快速傅里叶变换（FFT）能提供一个高效的计算手段。这往往比计算自相关函数要更高效和直接。

继续说白噪声。如果白噪声描述的是时间信号，那不具有周期性就是说，信号强度和时间不相关。

回忆卡尔曼滤波（Kalman Filter）的三个应用假设：

1.系统是线性的。

2.系统状态噪音是白噪音

3.系统状态噪音是高斯形式。

卡尔曼滤波中状态变量的后验概率可以表示如下：

其中

为t时刻的观察值，

为t时候的预测值，

为t时刻的估计值，也就是我们需要的值。事实上，这并不能算一个完全正确的贝叶斯推断公式，但是出于说明卡尔曼约束这样一个目的而言，我们权且用那个这样一个示意式来说明问题。

上式中，预测值

是有t-1时刻的估计值线性变换后得到的，使用了

卡尔曼滤波的第一个假设，系统是线性的。而

可表达t时刻下在真实值（或估计值）

条件下观测到

时的不确定度，即

似然率（likeihood）。所以，

是由t-1时刻状态得到的，而

是有t时刻状态得到的。而两者只有在独立的情况下，才能表达成这样一种直接相乘的形式。即

只有当随机变量X，Y独立时才成立。

和

互相独立，这就用了

卡尔曼滤波的第二个假设，系统状态噪音（不确定度）是白噪音，即，和时间不相关。

当然，卡尔曼滤波的最后表达式的得出是基于卡尔曼滤波的第三个假设，系统状态噪音（或不确定度uncertainly）是高斯形式。因为高斯函数和高斯函数相乘后，仍是一个高斯函数，并且该高斯函数的参数可以由原高斯函数完全给出。于是系统状态的后验概率就可以根据预测量及观测量的不确定度完全给出。

原文链接：http://www.360doc.com/content/16/0905/20/26322521_588652168.shtml

由于排版问题，重新整理放在这里。（侵删）