1.首先进行定义分析
频谱:频谱是频率谱密度的简称,是频率的分布曲线。复杂振荡分解为振幅不同和频率不同的谐振荡,这些谐振荡的幅值按频率排列的图形叫做频谱。频谱将对信号的研究从时域引入到频域,从而带来更直观的认识。
功率谱:功率谱是功率谱密度函数的简称,是在有限信号的情况下,单位频带范围内信号功率的变换状况,功率随频率而变化,即信号功率在频域的分布状况,从而表现成为功率谱,它是专门对功率能量的可用有限信号进行分析所表现的能量。它含有频谱的一些幅度信息,不过相位信息被舍弃掉了。
功率谱表示了信号功率随着频率的变化关系。 常用于功率信号(区别于能量信号)的表述与分析,其曲线(即功率谱曲线)一般横坐标为频率,纵坐标为功率。由于功率没有负值,所以功率谱曲线上的纵坐标也没有负数值,功率谱曲线所覆盖的面积在数值上等于信号的总功率(能量)。
对比分析:
相比之下,频谱极为不严格,主要是体现信号的平均变换,要求的只是一段时间平均量。
所以经常说在频谱信号不同的情况下,它的功率谱很可能是一样的。
2、方式
功率谱是对信号研究,不过它是从能量的方面来对信号研究的。
而频谱也是用来形容信号的,只是的表示方式变了,从时域转变成了频域表示,也就是说一种信号的表示方式不同而已。
功率谱与频谱和的区别归根结底就是信号、功率、能量三者之间的关联
3、计算
功率谱的计算需要信号先做自相关,然后再进行FFT运算。
频谱的计算则是将信号直接进行FFT就行了
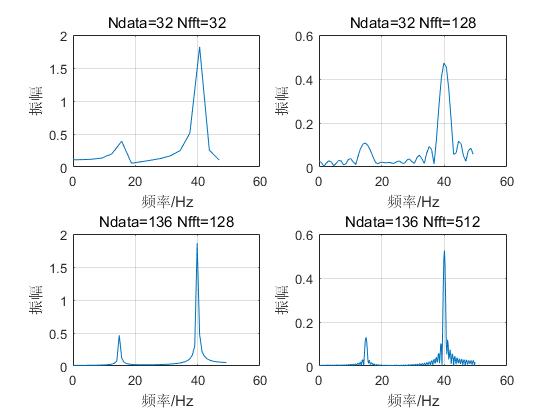
4.1频谱程序test
clf;fs=100; %采样频率
Ndata=32; %数据长度
N=32; %FFT的数据长度
n=0:Ndata-1;t=n/fs; %数据对应的时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %时间域信号
y=fft(x,N); %信号的Fourier变换
mag=abs(y); %求取振幅
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,1),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=32 Nfft=32');grid on;
Ndata=32; %数据个数
N=128; %FFT采用的数据长度
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=32 Nfft=128');grid on;
Ndata=136; %数据个数
N=128; %FFT采用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,3),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=136 Nfft=128');grid on;
Ndata=136; %数据个数
N=512; %FFT所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,4),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=136 Nfft=512');grid on;
%所有的去基线漂移的方法以及用pWelch方法求功率谱
clear
load('I:20190502datatestlfp4.mat');
sig_raw=lfp4;
NLen=length(sig_raw);
fs=1000;%采样频率,可从软件上设定
Ts=1/fs;%时间间隔为采样频率的倒数
n=0:1/fs:1;
nfft=1024;
window=hanning(250);
noverlap=20; %数据无重叠
range='onesided'; %频率间隔为[0 Fs/2],只计算一半的频率
%方法1:低通
%思路为低通得到趋势线,然后做差
fmaxd=5;%截止频率为3Hz
fmaxn=fmaxd/(fs/2);
[b,a]=butter(1,fmaxn,'low');
dd=filtfilt(b,a,lfp4);%通过5Hz低通滤波器的信号
Y1=lfp4-dd; %去除这一段信号,得到去基线漂移的信号
%绘图
figure()
subplot(3,1,1),plot(lfp4,'b');xlabel('原始信号');
subplot(3,1,2),plot(dd,'b');xlabel('趋势线');
subplot(3,1,3),plot(Y1,'b');xlabel('去除基线漂移的信号')
title('lowpass');
x1=Y1;
[Pxx_1,f_1]=pwelch(x1,window,noverlap,nfft,fs,range);
figure()
plot(f_1,Pxx_1);
xlim([0 100]);
xlabel('Frequency (Hz)');
title('Welch Power Spectral Density Estimate');
ylabel('Power/frequency (dB/Hz)');
grid on;
%method2 highpass
[bbw,abw]=cheby1(4,0.5,1.5/180,'high');
Y2=filtfilt(bbw,abw,lfp4);
figure()
subplot(2,1,1),plot(lfp4);xlabel('原始信号');
subplot(2,1,2),plot(Y2);xlabel('去除基线漂移的信号');
title('highpass');
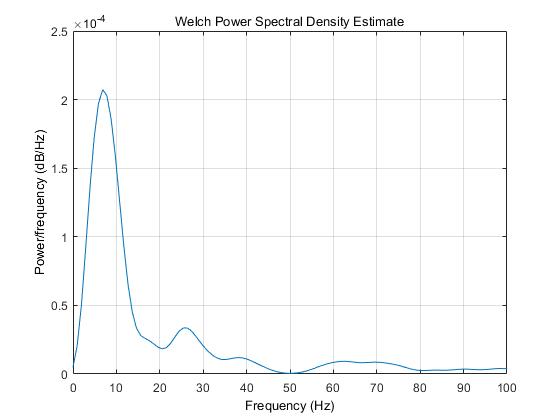
[Pxx_2,f_2]=pwelch(Y2,window,noverlap,nfft,fs,range);
figure()
plot(f_2,Pxx_2);
xlim([0 100]);
xlabel('Frequency (Hz)');
title('Welch Power Spectral Density Estimate');
ylabel('Power/frequency (dB/Hz)');
grid on;
%wavelet
x=lfp4;
y3 = DeBaseline_Wavelet(x);
figure()
subplot(211)
plot(x);
subplot(212);
plot(y3);
title('wavelet');
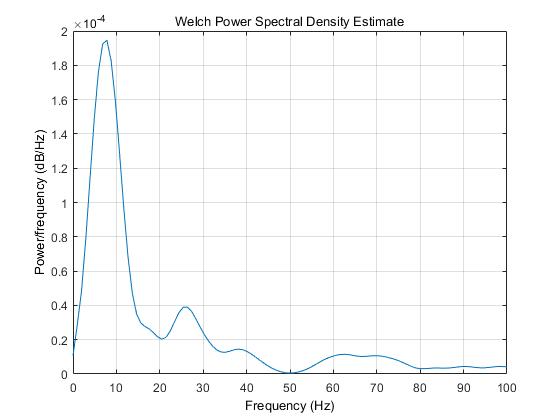
[Pxx_3,f_3]=pwelch(y3,window,noverlap,nfft,fs,range);
figure()
plot(f_3,Pxx_3);
xlim([0 100]);
xlabel('Frequency (Hz)');
title('Welch Power Spectral Density Estimate');
ylabel('Power/frequency (dB/Hz)');
grid on;
function y = DeBaseline_Wavelet(x)
s = x;
maxlev=7; %分解6尺度
wavename ='coif5'; %小波函数名称(需根据信号定)
[C,L] = wavedec(s,maxlev,wavename);
%提取分解后逼近系数和细节系数
A7=appcoef(C,L,wavename,7);
D1=detcoef(C,L,1);
D2=detcoef(C,L,2);
D3=detcoef(C,L,3);
D4=detcoef(C,L,4);
D5=detcoef(C,L,5);
D6=detcoef(C,L,6);
D7=detcoef(C,L,7);
%将第一尺度置零
D1= zeros(1,length(D1))'; %去掉高频噪声
D2= zeros(1,length(D2))';
A7=zeros(1,length(A7));
C2 = [A7,D7',D6',D5',D4',D3',D2',D1']; %新的系数
y = (waverec(C2,L,wavename))'; %重构去基线后信号
end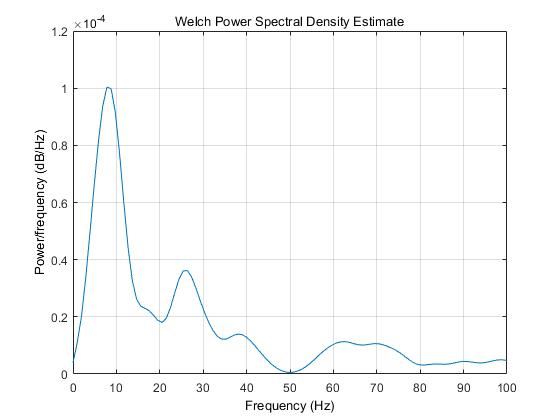
最后
以上就是殷勤金毛最近收集整理的关于频谱与功率谱的全部内容,更多相关频谱与功率谱内容请搜索靠谱客的其他文章。








发表评论 取消回复