matlab实验——信号和噪声产生及其功率谱分析

前言

本文的主要内容是利用matlab实现信号和噪声产生及其功率谱分析。

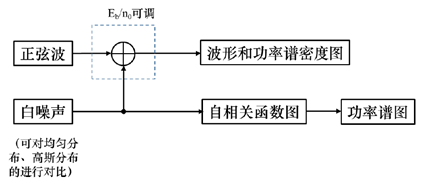
高斯白噪声：功率谱密度服从均匀分布，幅度分布服从高斯分布。
均匀白噪声：功率谱密度服从均匀分布，幅度分布服从均匀分布。
功率谱的计算需要信号先做自相关，然后再进行FFT运算。
频谱的计算则是将信号直接进行FFT就行了。
维纳-辛钦定理：任意一个均值为常数的广义平稳随机过程的功率谱密度是其自相关函数的傅立叶变换 。

一、高斯白噪声自相关函数及功率谱

1.matlab代码

%产生高斯白噪声
normal=0.1*randn(1,201); %产生均值为0,方差为0.01的高斯白噪声
[r,lags]=xcorr(normal); %做自相关
subplot(2,1,1);plot(lags,r);grid on;xlabel("高斯白噪声做自相关");
f=fftshift(fft(r));%频谱校正
x=(0:length(f)-1)*200/length(f)-100; %x轴
y=abs(f);
subplot(2,1,2);plot(x,y,'g');grid on;
axis([-100 100 -50 50]);xlabel("高斯白噪声功率谱");

2.运行结果

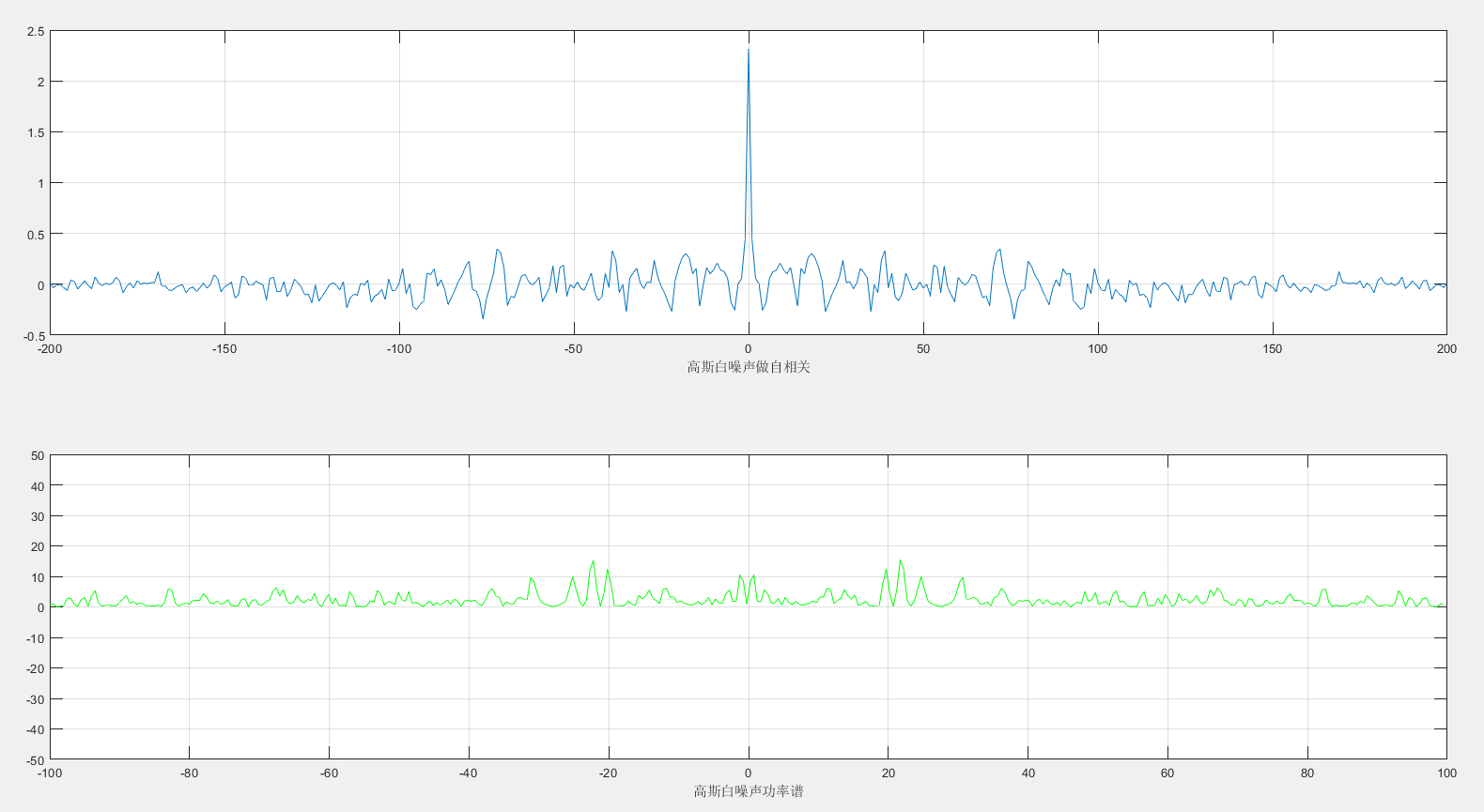
二、均匀白噪声自相关函数及功率谱

1.matlab代码

%产生均匀白噪声
uniform=-0.2+0.4*rand(1,201); %产生强度在-0.2到0.2之间的均匀白噪声
[r,lags]=xcorr(uniform); %做自相关
subplot(2,1,1);plot(lags,r);grid on;xlabel("均匀白噪声做自相关");
f=fftshift(fft(r));%频谱校正
x=(0:length(f)-1)*200/length(f)-100; %x轴
y=abs(f);
subplot(2,1,2);plot(x,y,'g');grid on;
axis([-100 100 -50 50]);xlabel("均匀白噪声功率谱");

2.运行结果

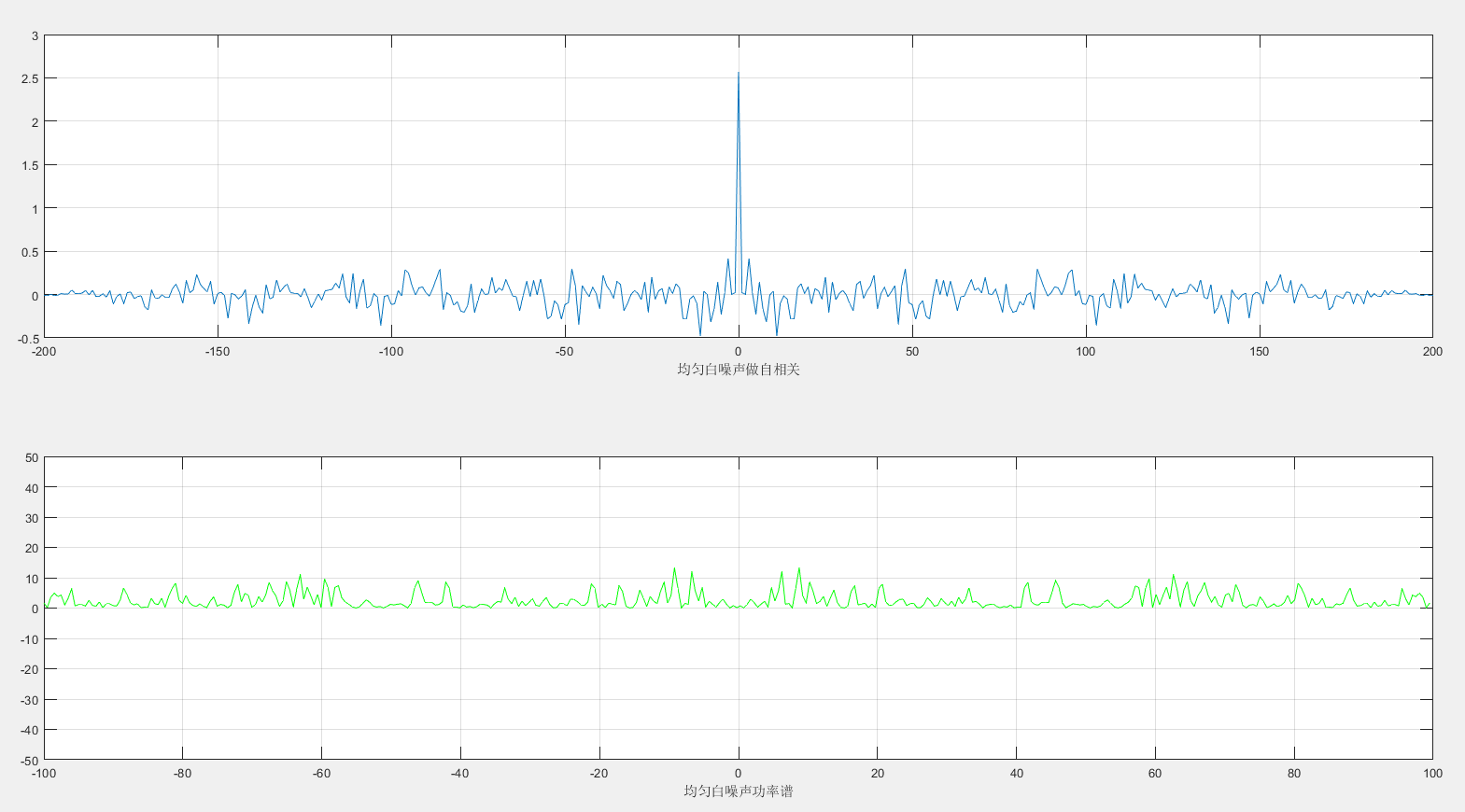
三、正弦波与高斯白噪声叠加

1.matlab代码

%产生正弦波
figure;
x=0:0.01:2;
y1=sin(10*pi*x);
subplot(3,1,1);plot(x,y1,'b');grid on;xlabel("正弦波的波形");
%产生高斯白噪声
normal=0.1*randn(1,201); %这里的长度必须与x的长度相同
subplot(3,1,2);plot(x,normal,'g');grid on;xlabel("高斯白噪声的波形");
y2=y1+normal; %将正弦波与高斯白噪声叠加
subplot(3,1,3);plot(x,y2,'r');grid on;xlabel("正弦波与高斯白噪声叠加后的波形");

figure;
fs=100;N=1024;%采样频率和数据点数
n=0:N-1;
f=n*fs/N; %频率序列
[r1,lags1]=xcorr(y1); %做自相关
[r2,lags2]=xcorr(normal);
[r3,lags3]=xcorr(y2);
yp1=fft(r1,N); %对信号进行快速傅里叶变换
yp2=fft(r2,N);
yp3=fft(r3,N);
mag1=abs(yp1); %求得傅里叶变换后的振幅
mag2=abs(yp2);
mag3=abs(yp3);
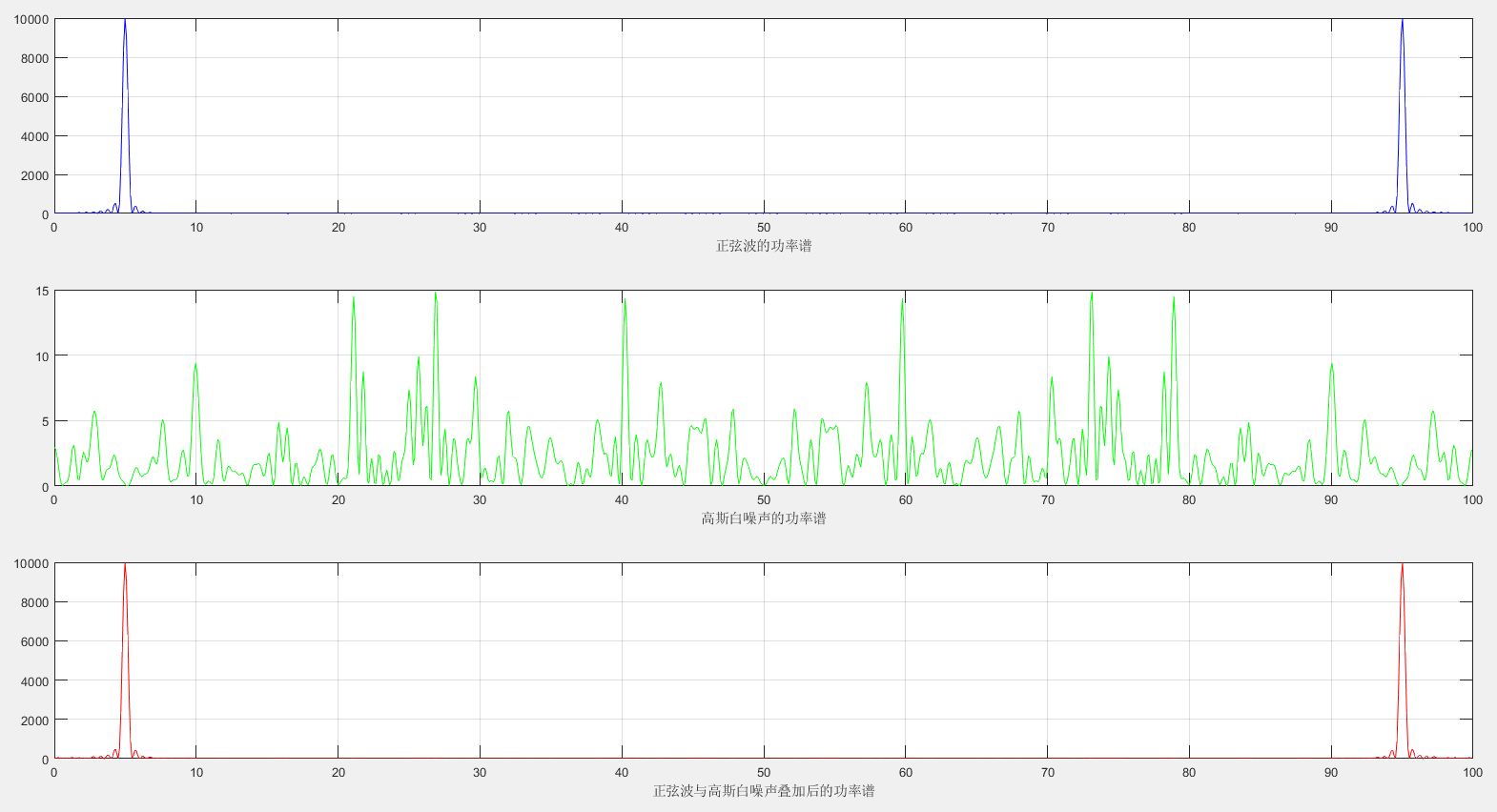
subplot(3,1,1);plot(f,mag1,'b');grid on; xlabel("正弦波的功率谱");
subplot(3,1,2);plot(f,mag2,'g');grid on; xlabel("高斯白噪声的功率谱");
subplot(3,1,3);plot(f,mag3,'r');grid on; xlabel("正弦波与高斯白噪声叠加后的功率谱");

2.运行结果

波形图如下：

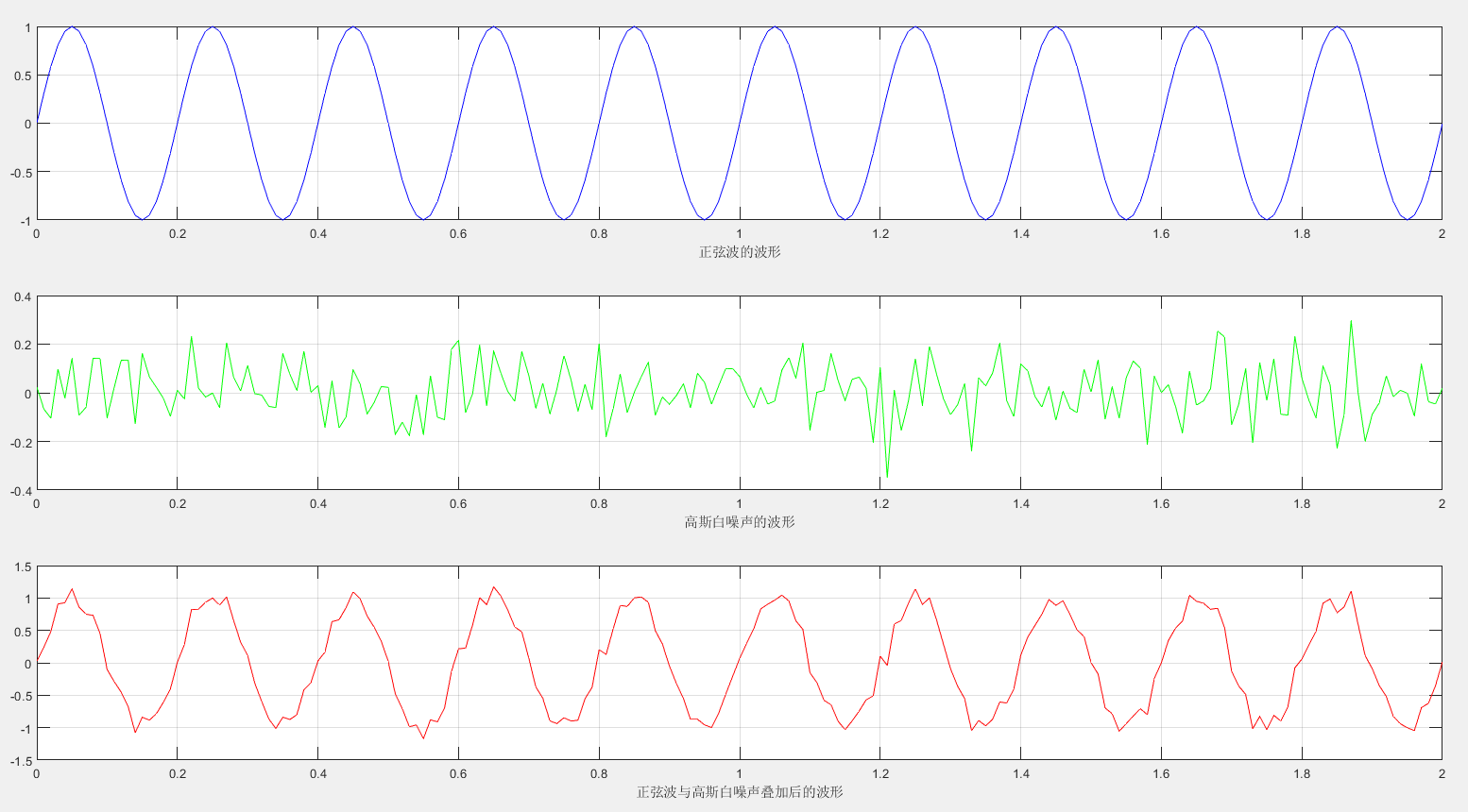
功率谱如下：

四、正弦波与均匀白噪声叠加

1.matlab代码

%产生正弦波
figure;
x=0:0.01:2;
y1=sin(10*pi*x);
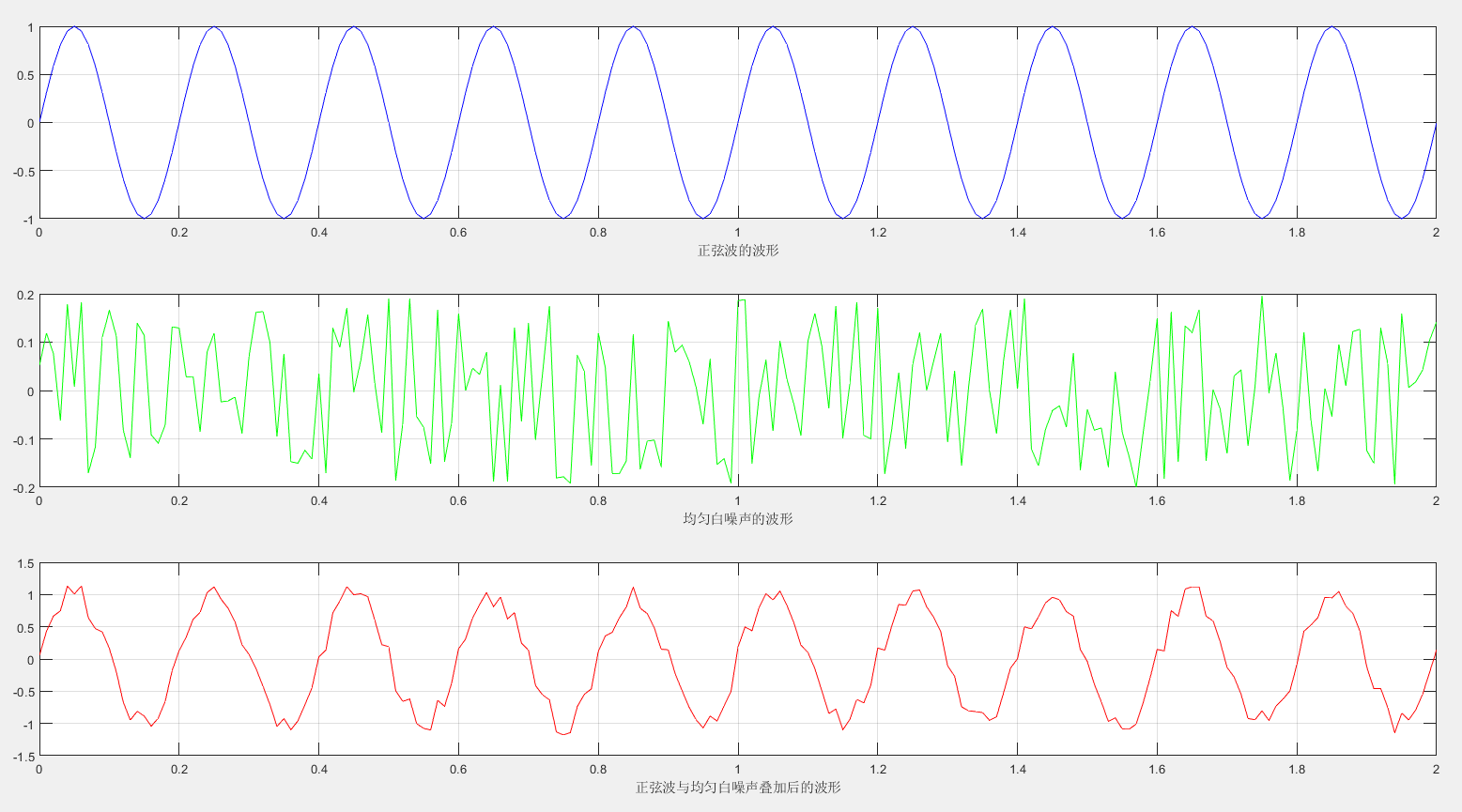
subplot(3,1,1);plot(x,y1,'b');grid on;xlabel("正弦波的波形");
%产生均匀白噪声
uniform=-0.2+0.4*rand(1,201); %产生强度在-0.2到0.2之间的均匀白噪声
subplot(3,1,2);plot(x,uniform,'g');grid on;xlabel("均匀白噪声的波形");
y2=y1+uniform; %将正弦波与均匀白噪声叠加
subplot(3,1,3);plot(x,y2,'r');grid on;xlabel("正弦波与均匀白噪声叠加后的波形");

figure;
fs=100;N=1024;%采样频率和数据点数
n=0:N-1;
f=n*fs/N; %频率序列
[r1,lags1]=xcorr(y1); %做自相关
[r2,lags2]=xcorr(uniform);
[r3,lags3]=xcorr(y2);
yp1=fft(r1,N); %对信号进行快速傅里叶变换
yp2=fft(r2,N);
yp3=fft(r3,N);
mag1=abs(yp1); %求得傅里叶变换后的振幅
mag2=abs(yp2);
mag3=abs(yp3);
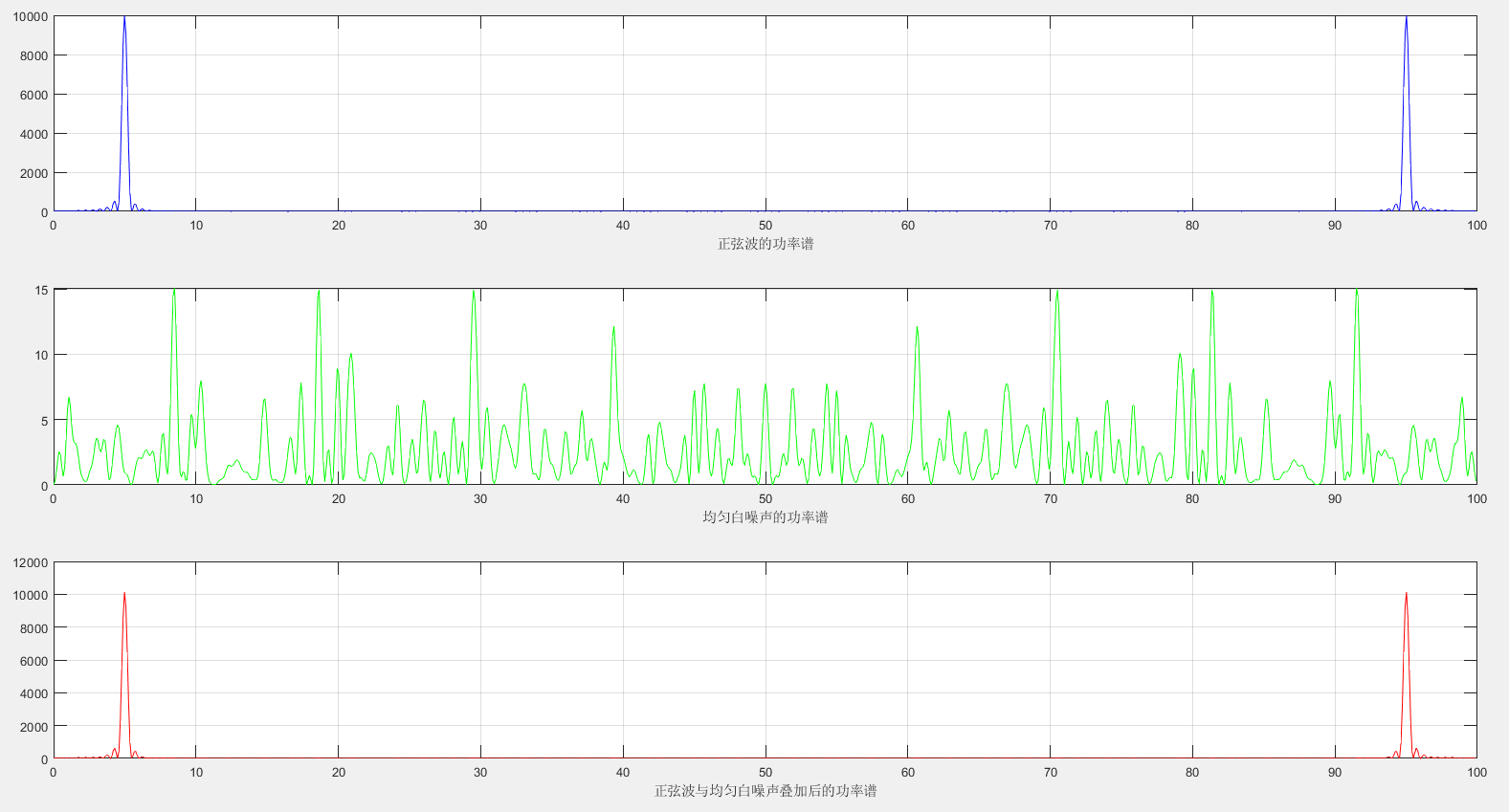
subplot(3,1,1);plot(f,mag1,'b');grid on; xlabel("正弦波的功率谱");
subplot(3,1,2);plot(f,mag2,'g');grid on; xlabel("均匀白噪声的功率谱");
subplot(3,1,3);plot(f,mag3,'r');grid on; xlabel("正弦波与均匀白噪声叠加后的功率谱");

2.运行结果

波形图如下：

功率谱如下：

总结

以上就是用matlab进行信号和噪声产生及其功率谱分析的所有内容了，希望对你有帮助！

最后

以上就是明理电脑为你收集整理的matlab实验——信号和噪声产生及其功率谱分析的全部内容，希望文章能够帮你解决matlab实验——信号和噪声产生及其功率谱分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。