概述
因为最近论文有信息量很大的结果需要展示，如果用常用的折线图或者柱状图很难集中且全面的展示实验结果，和老板讨论之后了解到--箱线图这种神奇的图形展示方式。边学边用~记录在这里~也给有论文写作需要的小伙伴们一个参考~
1. 什么是箱线图？
箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。
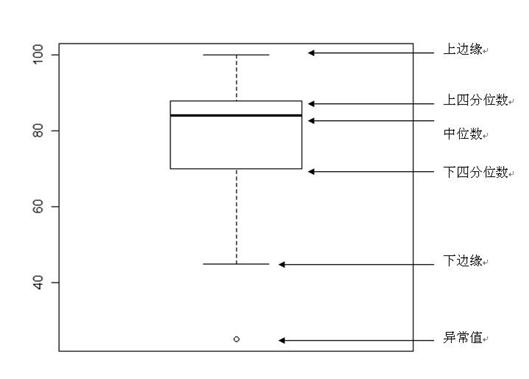
绘制步骤：
（1）计算上四分位数（Q3），中位数，下四分位数（Q1）
（2）计算上四分位数和下四分位数之间的差值，即四分位数差（IQR，interquartile range）Q3-Q1
（3）绘制箱线图的上下范围，上限为上四分位数，下限为下四分位数。在箱子内部中位数的位置绘制横线。
（4）大于上四分位数1.5倍四分位数差的值，或者小于下四分位数1.5倍四分位数差的值，划为异常值（outliers），即Q3+1.5IQR（四分位间距）和Q1－1.5IQR处画两条与中位线一样的线段，这两条线段为异常值截断点，称其为内限；
（5）异常值之外，最靠近上边缘和下边缘的两个值处，画横线，作为箱线图的触须。 即在Q3+3IQR和Q1－3IQR处画两条线段，称其为外限。
（6）极端异常值，即超出四分位数差3倍距离的异常值，用实心点表示；较为温和的异常值，即处于1.5倍-3倍四分位数差之间的异常值，用空心点表示。
（7）从矩形盒两端边向外各画一条线段直到不是异常值的最远点，表示该批数据正常值的分布区间。
（8）用“〇”标出温和的异常值，用“*”标出极端的异常值。相同值的数据点并列标出在同一数据线位置上，不同值的数据点标在不同数据线位置上。
（9）为箱线图添加名称，数轴等
5个参数：
下边缘（Q1），表示最小值；
下四分位数（Q2），又称“第一四分位数”，等于该样本中所有数值由小到大排列后第25%的数字；
中位数（Q3），又称“第二四分位数”等于该样本中所有数值由小到大排列后第50%的数字；
上四分位数（Q4），又称“第三四分位数”等于该样本中所有数值由小到大排列后第75%的数字；
上边缘（Q5），表述最大值。
=
=
=
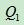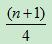
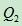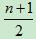
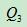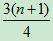
2. 箱形图的作用
- 识别数据异常值 箱形图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1－1.5IQR或大于Q3+1.5IQR的值。虽然这种标准有点任意性，但它来源于经验判断，经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知，基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的，而均值和标准差的耐抗性极小，异常值本身会对它们产生较大影响，这样产生的异常值个数不会多于总数0.7%。显然，应用这种方法于非正态分布数据中判断异常值，其有效性是有限的。箱形图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；另一方面，箱形图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱形图识别异常值的结果比较客观。由此可见，箱形图在识别异常值方面有一定的优越性。
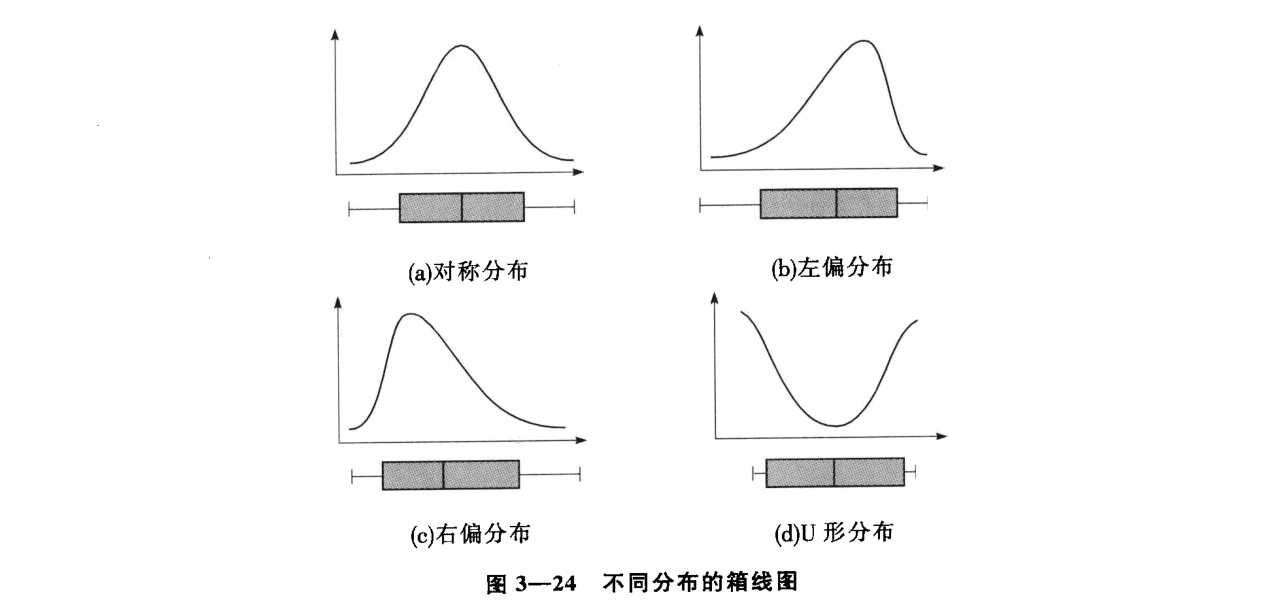
- 判断数据偏态和尾重 比较标准正态分布、不同自由度的t分布和非对称分布数据的箱形图的特征，可以发现：对于标准正态分布的大样本，只有 0.7%的值是异常值,中位数位于上下四分位数的中央,箱形图的方盒关于中位线对称。选取不同自由度的t分布的大样本，代表对称重尾分布，当t分布的自由度越小，尾部越重，就有越大的概率观察到异常值。以卡方分布作为非对称分布的例子进行分析，发现当卡方分布的自由度越小，异常值出现于一侧的概率越大，中位数也越偏离上下四分位数的中心位置，分布偏态性越强。异常值集中在较小值一侧，则分布呈现左偏态；；异常值集中在较大值一侧，则分布呈现右偏态。
3. 比较几批数据的形状
同一数轴上，几批数据的箱形图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。在一批数据中，哪几个数据点出类拔萃，哪些数据点表现不及一般，这些数据点放在同类其它群体中处于什么位置，可以通过比较各箱形图的异常值看出。各批数据的四分位距大小，正常值的分布是集中还是分散，观察各方盒和线段的长短便可明了。每批数据分布的偏态如何，分析中位线和异常值的位置也可估计出来。箱形图结合这些分析方法用于质量管理、人事测评、探索性数据分析等统计分析活动中去，有助于分析过程的简便快捷，其作用显而易见
plt.boxplot(x, notch=None, sym=None, vert=None,
whis=None, positions=None, widths=None,
patch_artist=None, meanline=None, showmeans=None,
showcaps=None, showbox=None, showfliers=None,
boxprops=None, labels=None, flierprops=None,
medianprops=None, meanprops=None,
capprops=None, whiskerprops=None)
x：指定要绘制箱线图的数据；
notch：是否是凹口的形式展现箱线图，默认非凹口；
sym：指定异常点的形状，默认为+号显示；
vert：是否需要将箱线图垂直摆放，默认垂直摆放；
whis：指定上下须与上下四分位的距离，默认为1.5倍的四分位差；
positions：指定箱线图的位置，默认为[0,1,2…]；
widths：指定箱线图的宽度，默认为0.5；
patch_artist：是否填充箱体的颜色；
meanline：是否用线的形式表示均值，默认用点来表示；
showmeans：是否显示均值，默认不显示；
showcaps：是否显示箱线图顶端和末端的两条线，默认显示；
showbox：是否显示箱线图的箱体，默认显示；
showfliers：是否显示异常值，默认显示；
boxprops：设置箱体的属性，如边框色，填充色等；
labels：为箱线图添加标签，类似于图例的作用；
filerprops：设置异常值的属性，如异常点的形状、大小、填充色等；
medianprops：设置中位数的属性，如线的类型、粗细等；
meanprops：设置均值的属性，如点的大小、颜色等；
capprops：设置箱线图顶端和末端线条的属性，如颜色、粗细等；
whiskerprops：设置须的属性，如颜色、粗细、线的类型等；
# 导入第三方模块
import pandas as pd
import matplotlib.pyplot as plt
# 读取Titanic数据集
titanic = pd.read_csv('titanic_train.csv')
# 检查年龄是否有缺失
any(titanic.Age.isnull())
# 不妨删除含有缺失年龄的观察
titanic.dropna(subset=['Age'], inplace=True)
# 设置图形的显示风格
plt.style.use('ggplot')
# 设置中文和负号正常显示
plt.rcParams['font.sans-serif'] = 'Microsoft YaHei'
plt.rcParams['axes.unicode_minus'] = False
# 绘图：整体乘客的年龄箱线图
plt.boxplot(x = titanic.Age, # 指定绘图数据
patch_artist=True, # 要求用自定义颜色填充盒形图，默认白色填充
showmeans=True, # 以点的形式显示均值
boxprops = {'color':'black','facecolor':'#9999ff'}, # 设置箱体属性，填充色和边框色
flierprops = {'marker':'o','markerfacecolor':'red','color':'black'}, # 设置异常值属性，点的形状、填充色和边框色
meanprops = {'marker':'D','markerfacecolor':'indianred'}, # 设置均值点的属性，点的形状、填充色
medianprops = {'linestyle':'--','color':'orange'}) # 设置中位数线的属性，线的类型和颜色
# 设置y轴的范围
plt.ylim(0,85)
# 去除箱线图的上边框与右边框的刻度标签
plt.tick_params(top='off', right='off')
# 显示图形
plt.show()
---------------------
参考：https://blog.csdn.net/kevinelstri/article/details/52937236
https://blog.csdn.net/ZengHaihong/article/details/53291372
https://blog.csdn.net/roguesir/article/details/78249864
http://blog.sina.com.cn/s/blog_e126b6140101kvq2.html
最后
以上就是爱笑网络为你收集整理的Box plot (箱线图) 解读以及Python实现的全部内容，希望文章能够帮你解决Box plot (箱线图) 解读以及Python实现所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复