系列文章目录

第1章 MATLAB R2018b环境
第2章 MATLAB 数值计算
第3章 MATLAB符号计算
第4章 MATLAB计算的可视化和GUI设计
第5章 MATLAB程序设计
第6章 线性控制系统分析与设计
第7章 Simulink仿真环境
第8章 MATLAB高级应用

第三章、MATLAB符号计算

前言

本次内容主要介绍符号极限、微积分和级数求和等内容。

16、符号极限、微积分和级数求和

16.1符号极限

假定符号表达式的极限存在，Symbolic Math Toolbox提供了直接求表达式极限的函数limit，函数limit的基本用法如下所示：
limt(f):对x求趋近于0的极限
limt(f,x,a):对x求趋近于a的极限,当左右极限不相等时极限不存在
limt(f,x,a,left):对x求左趋近于a的极限
limt(f,x,a,right):对x求右趋近于a的极限

16.2符号微分

函数diff是用来求符号表达式的微分。
diff(f) %求f对自由变量的一阶微分
diff(f,t) %求f对符号变量t的一阶微分
difi(f,n) %求f对自由变量的n阶微分
diff(f,t,n) %求f对符号变量t的n阶微分

微分函数diff也可以用于符号矩阵,其结果是对矩阵的每一个元素进行微分运算。
diff还可以用于对数组中的元素进行逐项求差值。

16.3符号积分

积分分为定积分和不定积分。运用函数 int可以求得符号表达式的积分，即我出一个符号表达式F，使得 diff(F)=f，也可以说是求微分的逆运算。
语法:int(f,‘t’) %求符号变量t的不定积分
int(f, ‘t’,a,b) %求符号变量t的积分
int(f, ‘t’, ‘m’, ‘n’) %求符号变量t的积分
说明: t为符号变量，若t省略则为默认自由变量; a和b为数值，[a,b]为积分区间;m和n为符号对象，[m,n]为积分区间。与符号微分相比，符号积分复杂得多。函数的积分有时可能不存在，即使存在，也可能由于限于很多条件，MATLAB无法顺利得出。当MATLAB不能找到积分时，它将给出警告提示并返回该函数的原表达式。

16.4符号级数

当符号表达式的级数和存在时，在 MATLAB中可以使用symsum和 taylor 函数进行求级数的运算。
1.symsum函数语法:
symsum(s,x,a,b) %计算表达式s的级数和
说明:x为自变量，若x省略则默认为对自由变量求和; s为符号表达式;[a,b]为参数x的取值范围。

2.taylor 函数
泰勒级数的计算使用taylor函数。
语法:taylor (F,x,n) %求泰勒级数展开
说明:x为自变量，F为符号表达式;对F进行泰勒级数展开至n项，若参数n省略则默认展开前5项。
泰勒级数还可以使用可视化的泰勒级数计算器，在命令窗口中输入命令“taylortool”,就会出现泰勒级数计算器窗口，如下图所示。

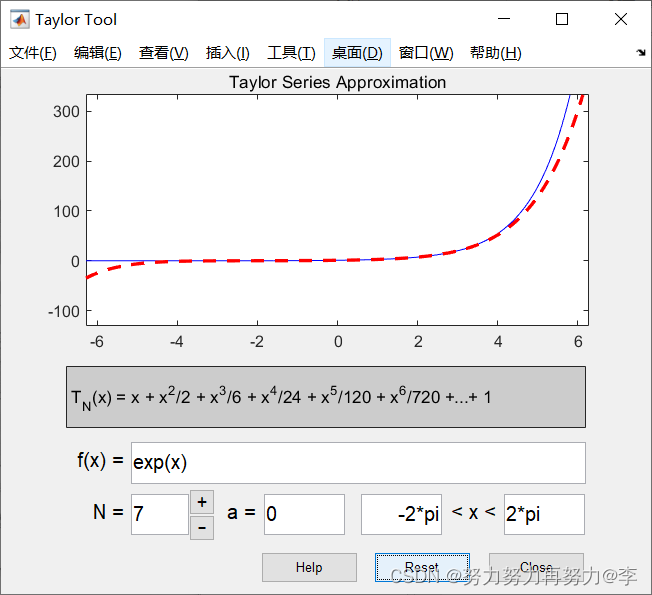
图中蓝色的曲线为f(x)的曲线，红色的点线为泰勒级数TN(x)的曲线。在泰勒级数计算器图形窗口中，各参数的说明如下。
f(x):需要使用泰勒级数逼近的函数，可以在命令窗口中直接输入“taylortool('f(x))”命令，也可以在上图窗口中输入f(x)表达式;
N:泰勒级数展开的阶次，默认为7;
a:泰勒级数的展开点，默认为0;
x的范围:默认为-2pi～2pi。

总结

文章内容来自MATLAB实用教程/郑阿奇主编，ISBN 978-7-121-29138-8。若有侵权行为，请联系我自行删除。

最后

以上就是沉默裙子为你收集整理的MATLAB R2018b学习笔记（16）系列文章目录第三章、MATLAB符号计算前言16、符号极限、微积分和级数求和总结的全部内容，希望文章能够帮你解决MATLAB R2018b学习笔记（16）系列文章目录第三章、MATLAB符号计算前言16、符号极限、微积分和级数求和总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。