单位冲激函数性质

筛选性质

设信号$s\left(t\right)$是一个在$t=t_0$处连续的函数，则有
$$s\left(t\right)\delta (t-t_0)=s\left(t_0\right)\delta (t-t_0)$$

取样性质

设信号$s\left(t\right)$是一个在$t=t_0$处连续的函数，则有
$${\int }_{-\infty }^{+\infty }s\left(t\right)\delta (t-t_0)dt=s(t_0)$$
特别地，当$t_0=0$时
$${\int }_{-\infty }^{+\infty }s\left(t\right)\delta (t)dt=s(0)$$

尺度性质证明

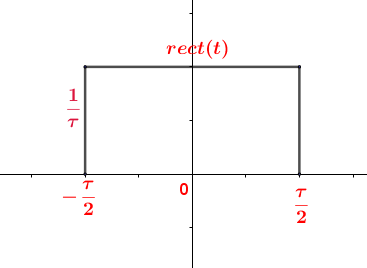
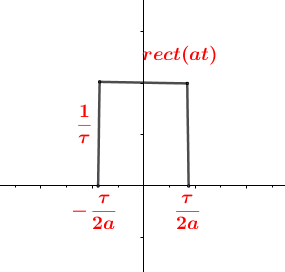
由上图可知矩形的面积如下：
$$\begin{array}{rl}S[rect(t)]& =1\\ S[rect(at)]& =\frac{1}{|a|}\end{array}$$
当$\tau \to 0$时，有
$$\begin{array}{rl}\underset{\tau \to 0}{\lim }rect(t)& =\delta (t)\\ \underset{\tau \to 0}{\lim }rect(at)& =\frac{1}{|a|}\delta (t)\end{array}$$
证明：$\delta (at-b)=\frac{1}{|a|}\delta (t-\frac{b}{a})$

当$a>0$时，令$at-b=x$
$$\begin{array}{rl}{\int }_{-\infty }^{+\infty }s\left(t\right)\delta (at-b)dt& =\frac{1}{a}{\int }_{-\infty }^{+\infty }s\left(\frac{1}{a}x+\frac{b}{a}\right)\delta (x)dx\\ & =\frac{1}{a}s\left(\frac{b}{a}\right)\end{array}$$
根据取样性质
$${\int }_{-\infty }^{+\infty }\frac{1}{a}s\left(t\right)\delta (t-\frac{b}{a})dt=\frac{1}{a}s\left(\frac{b}{a}\right)$$
当$a<0$时，令$-|a|t-b=x$
$$\{\begin{array}{l}t:-\infty \to +\infty \\ x:+\infty \to -\infty \end{array}$$

$$\begin{array}{rl}{\int }_{-\infty }^{+\infty }s\left(t\right)\delta (at-b)dt& =-\frac{1}{|a|}{\int }_{+\infty }^{-\infty }s\left(-\frac{1}{|a|}x-\frac{b}{|a|}\right)\delta (x)dx\\ & =\frac{1}{|a|}{\int }_{-\infty }^{+\infty }s\left(-\frac{1}{|a|}x-\frac{b}{|a|}\right)\delta (x)dx\\ & =\frac{1}{|a|}s\left(-\frac{b}{|a|}\right)\end{array}$$

同样根据取样性质，且$|a|=-a$
$${\int }_{-\infty }^{+\infty }\frac{1}{|a|}s\left(t\right)\delta (t+\frac{b}{|a|})dt=\frac{1}{|a|}s\left(-\frac{b}{|a|}\right)$$
得证。

根据冲激函数尺度性质证明$\cos (w_{0}t)$的傅里叶变换

根据欧拉公式
$$\cos (wt)=\frac{1}{2}(e^{jwt}+e^{-jwt})$$
其Fourier变换为
$$\begin{array}{rl}G(f)& ={\int }_{+\infty }^{-\infty }\cos (w_{0}t)e^{-jwt}dt\\ & =\frac{1}{2}{\int }_{+\infty }^{-\infty }(e^{j{w}_{0}t}+e^{-j{w}_{0}t})e^{-jwt}dt\\ & =\frac{1}{2}{\int }_{+\infty }^{-\infty }(e^{-j2\pi (f-f_0)t}+e^{-j2\pi (f+f_0)t})dt\\ & =\frac{1}{2}[\delta (f-f_0)+\delta (f+f_0)]\end{array}$$
根据冲激函数尺度性质
$$\begin{array}{rl}\delta (w-w_0)& =\delta [2\pi (f-f_0)]\\ & =\frac{1}{2\pi }\delta [(f-f_0)]\end{array}$$
所以
$$G(w)=\pi [\delta (w-w_0)+\delta (w+w_0)]$$

最后

以上就是殷勤哈密瓜最近收集整理的关于单位冲激函数性质的全部内容，更多相关单位冲激函数性质内容请搜索靠谱客的其他文章。